Похожие презентации:
Взаимное пересечение поверхностей
1. Лекция
Взаимные пересеченияповерхностей
2. Пересечение поверхностей
Пример модели3.
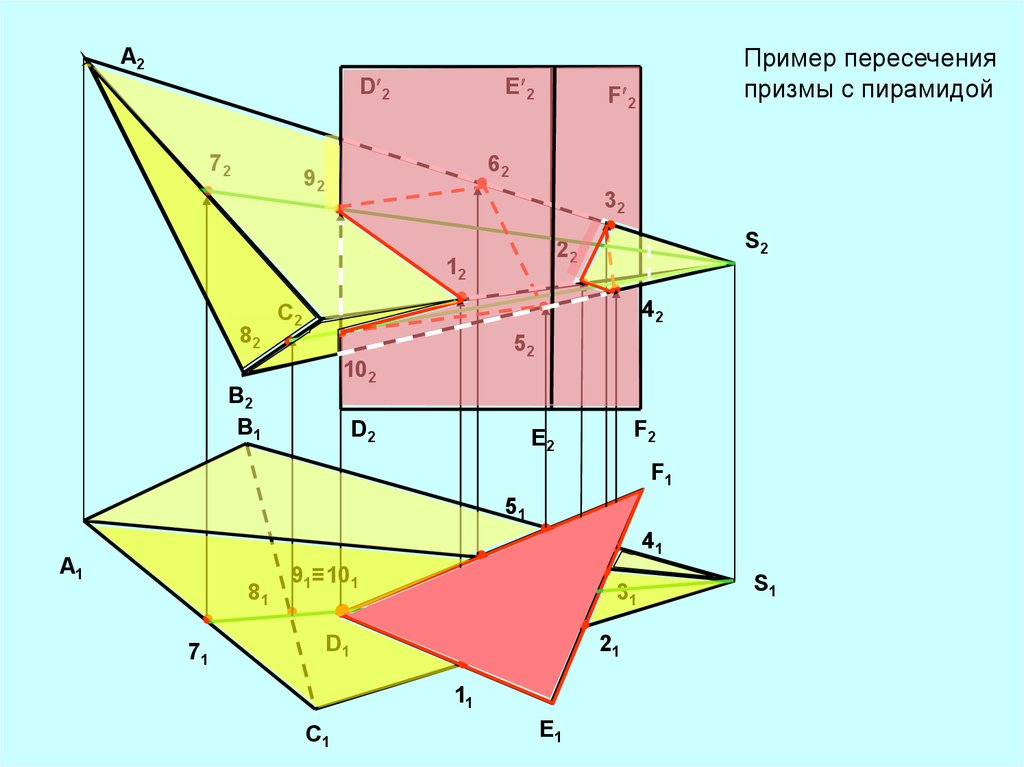
Пример пересеченияпризмы с пирамидой
A2
D 2
72
E 2
F 2
62
92
32
12
82
S2
22
42
C2
52
102
B2
B1
D2
F2
E2
F1
51
41
A1
81
71
91≡101
61
31
D1
21
11
C1
E1
S1
4. Применение вспомогательных секущих плоскостей.
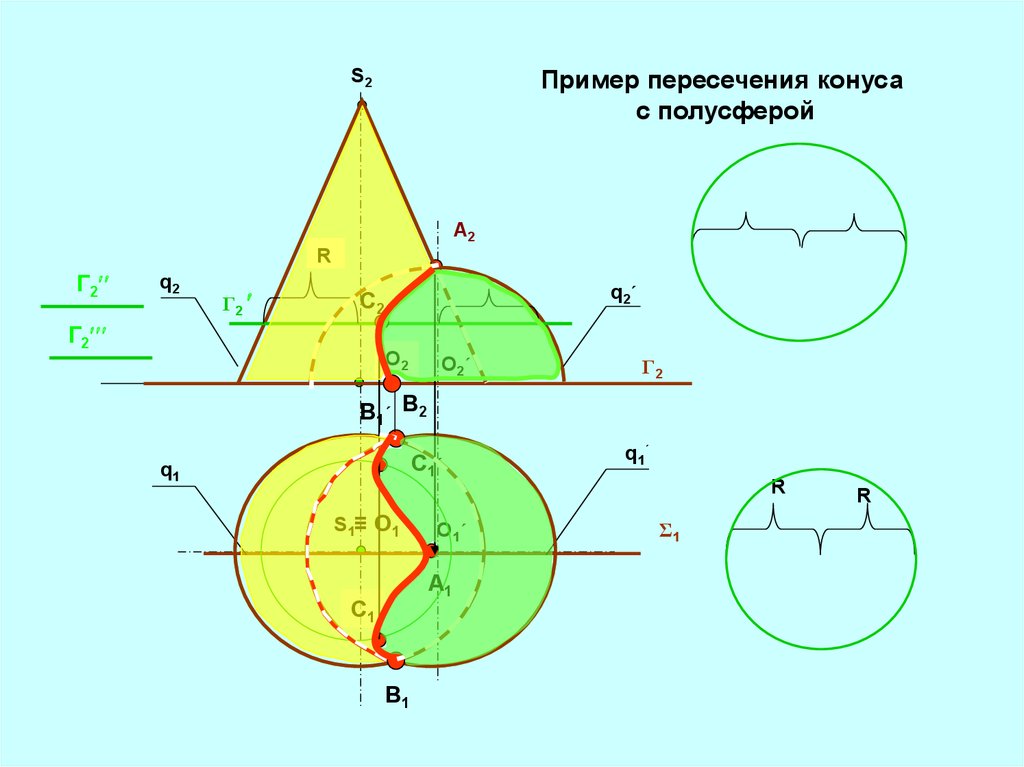
Пример пересечения конусас полусферой
S2
A2
R
Г2
q2
Γ2
q2´
C2
Г2
O2
O2´
Γ2
B1´ B2
C1´
q1
S1≡ O1
O1´
A1
C1
B1
q1´
R
Σ1
R
5. Пример модели
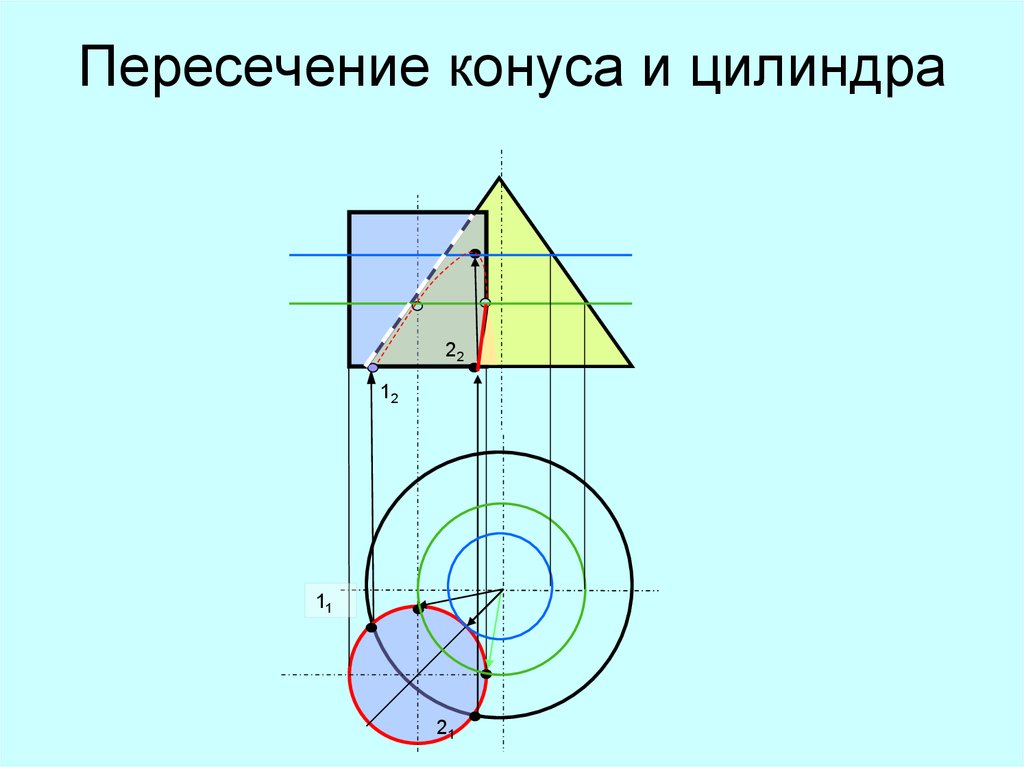
Пересечение конуса и цилиндра22
12
11
21
6.
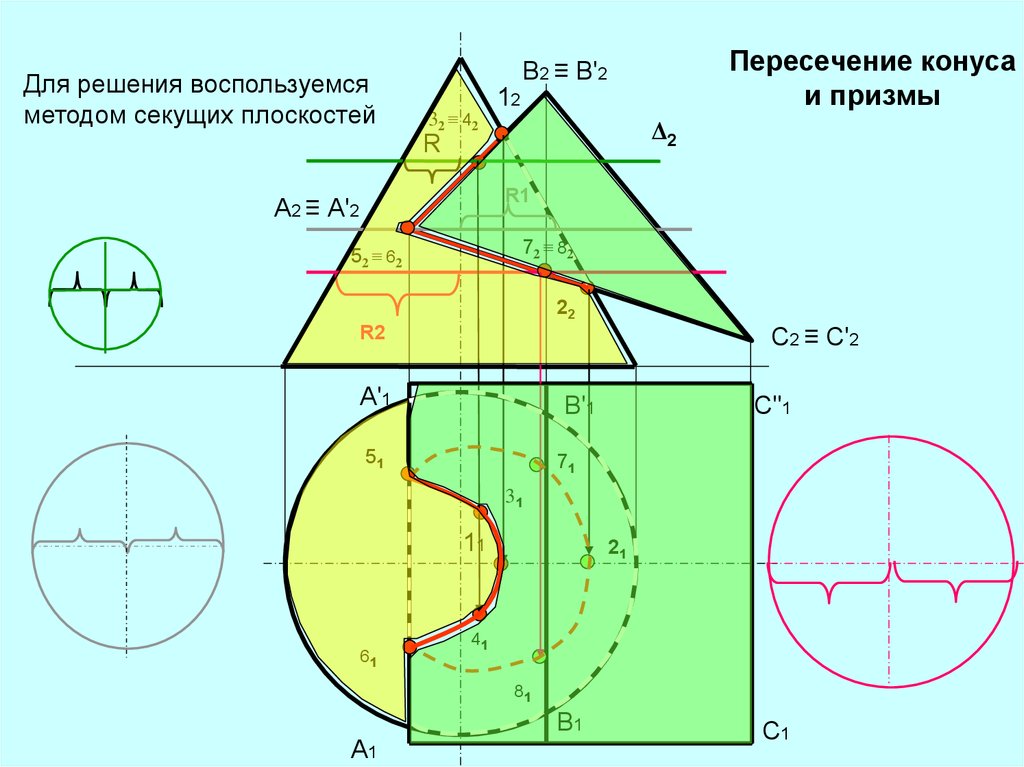
Для решения воспользуемсяметодом секущих плоскостей
Пересечение конуса
и призмы
В2 ≡ В'2
32 ≡ 42
12
Δ2
R
R1
А2 ≡ А'2
72 ≡ 82
52 ≡ 62
22
С2 ≡ С'2
R2
А'1
В'1
51
С''1
71
31
11
61
21
41
81
А1
В1
С1
7. Применение вспомогательных секущих плоскостей.
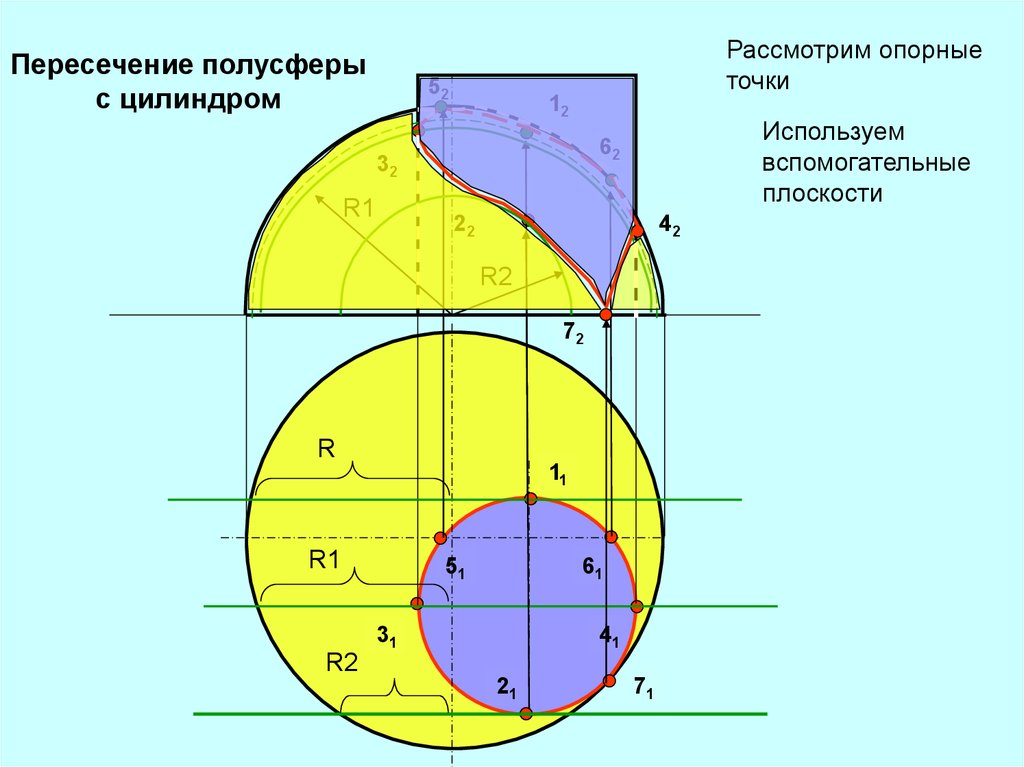
Пересечение полусферыс цилиндром
Рассмотрим опорные
точки
52
12
32
R1
Используем
вспомогательные
плоскости
62
22
42
R2
72
R
11
R1
51
61
31
41
R2
21
71
8.
СООСНЫЕ ПОВЕРХНОСТИ ВРАЩЕНИЯ• Соосными • Теорема. Две соосные
называются
поверхности вращения
поверхности
пересекаются по
вращения,
окружностям, число которых
имеющие
равно числу точек
общую ось.
пересечения главных
полумеридианов
поверхностей
9.
10.
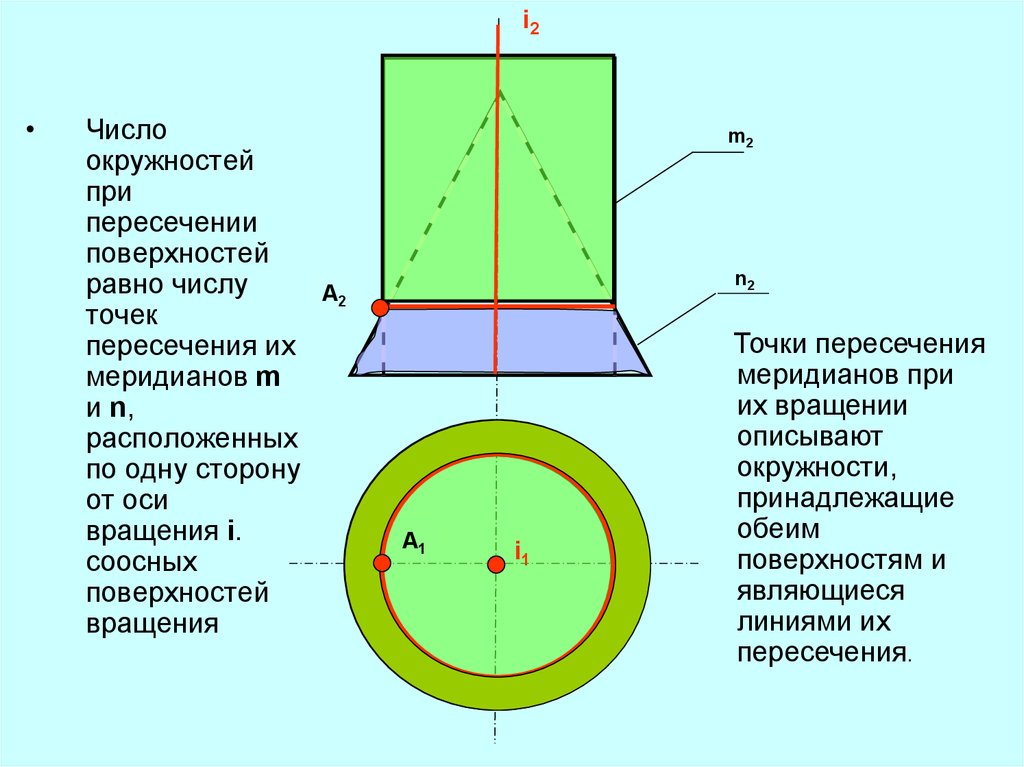
i2Число
окружностей
при
пересечении
поверхностей
равно числу
точек
пересечения их
меридианов m
и n,
расположенных
по одну сторону
от оси
вращения i.
соосных
поверхностей
вращения
m2
n2
A2
A1
i1
Точки пересечения
меридианов при
их вращении
описывают
окружности,
принадлежащие
обеим
поверхностям и
являющиеся
линиями их
пересечения.
11.
СПОСОБ ВСПОМОГАТЕЛЬНЫХ СФЕР• Для построения линии пересечения
поверхностей вращения, имеющих
круговые сечения, в ряде случаев в
качестве вспомогательных
поверхностей целесообразно
использовать сферы.
Разновидности способа включают в
себя: способ концентрических сфер
и способ эксцентрических сфер.
12. Пересечение конуса и цилиндра
Способконцентрических сфер
применяется, если:
• - оси поверхностей
пересекаются;
• - есть общая
плоскость симметрии;
• - если способ
вспомогательных
секущих плоскостей
не дает простого
решения.
Способ эксцентрических
сфер применяется,
если:
• - оси поверхностей
скрещиваются;
• - есть общая
плоскость симметрии;
• - каждая из
поверхностей имеет
семейство круговых
сечений;
• - если способ
вспомогательных
секущих плоскостей
не дает простого
решения.
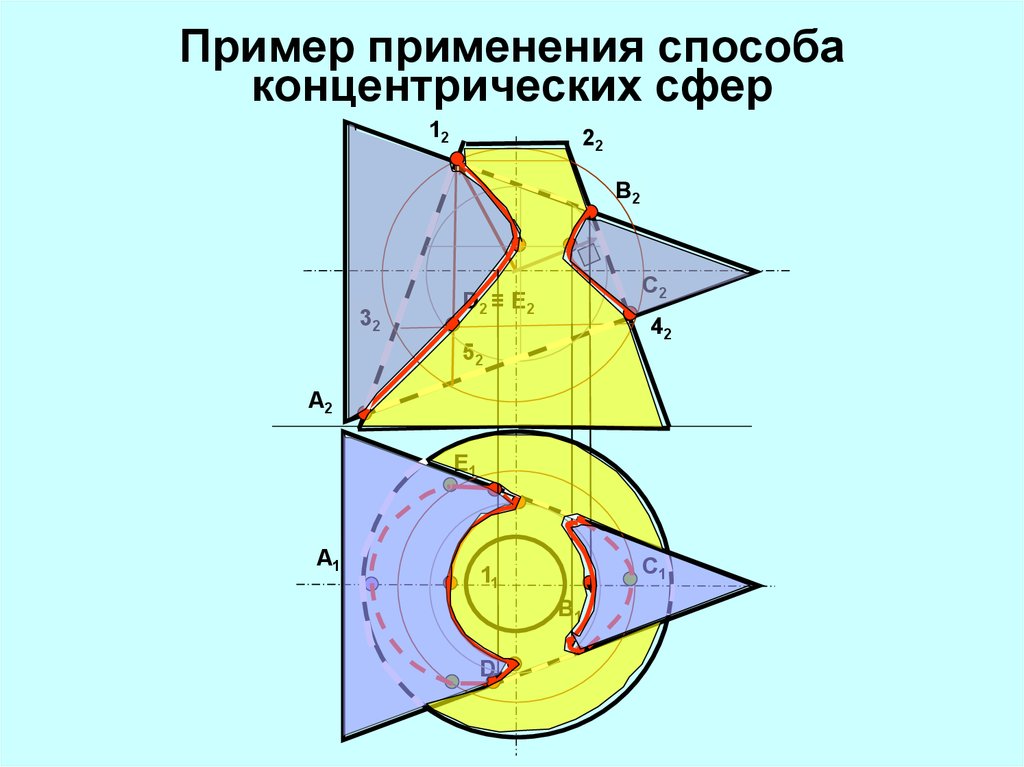
13.
Пример применения способаконцентрических сфер
12
22
B2
32
C2
D2 ≡ E2
42
52
A2
E1
A1
C1
11
B1
D1
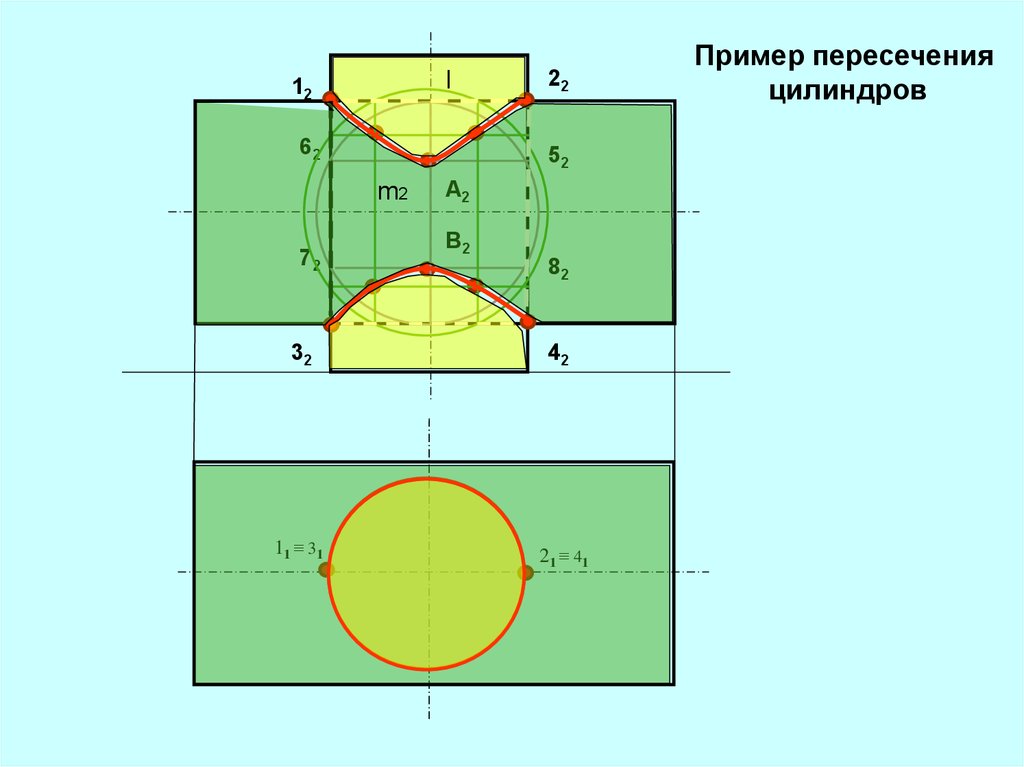
14.
l12
62
52
m2
72
22
A2
B2
82
32
42
1 1 ≡ 31
21 ≡ 41
Пример пересечения
цилиндров
15. СООСНЫЕ ПОВЕРХНОСТИ ВРАЩЕНИЯ
Применение вспомогательныхэксцентрических сфер.
• Такие сферы применяют, если:
• Одна из пересекающихся поверхностей поверхность вращения, другая поверхность имеет
круговые сечения;
• Две поверхности имеют общую плоскость
симметрии (т. е. ось поверхности вращения и
центры круговых сечений второй поверхности
принадлежат одной плоскости - плоскости их
симметрии);
• Плоскость симметрии параллельна плоскости
проекций ( это условие при необходимости может
быть обеспечено преобразованием чертежа).
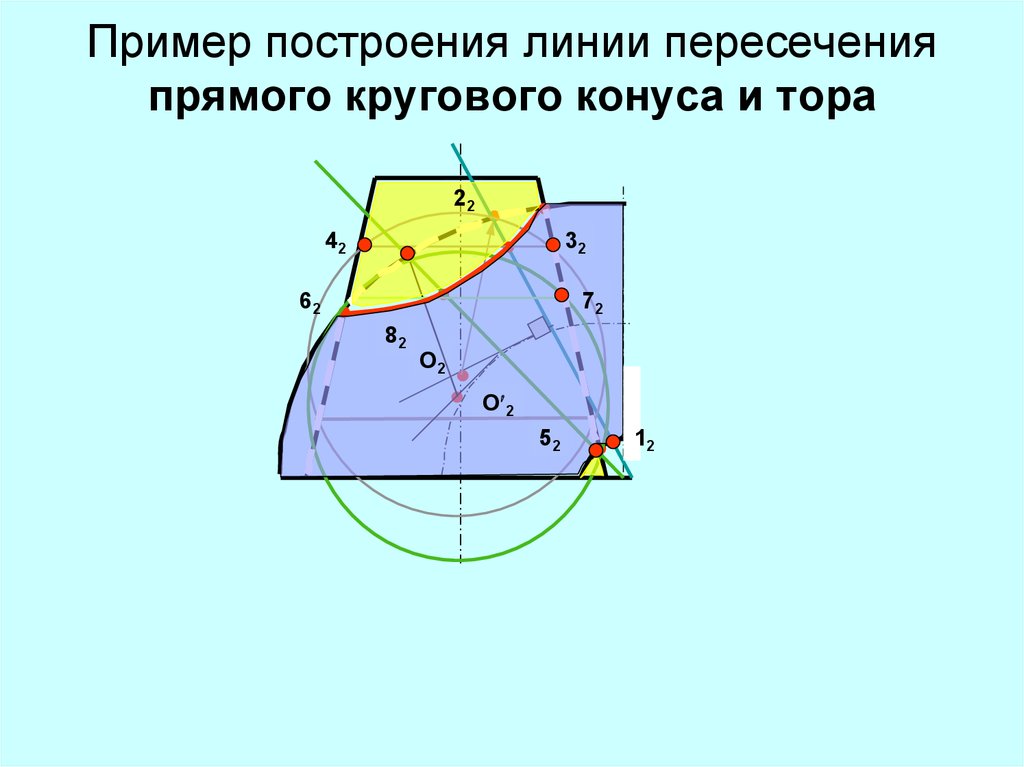
16.
Пример построения линии пересеченияпрямого кругового конуса и тора
22
42
32
62
72
82
O2
O 2
52
12
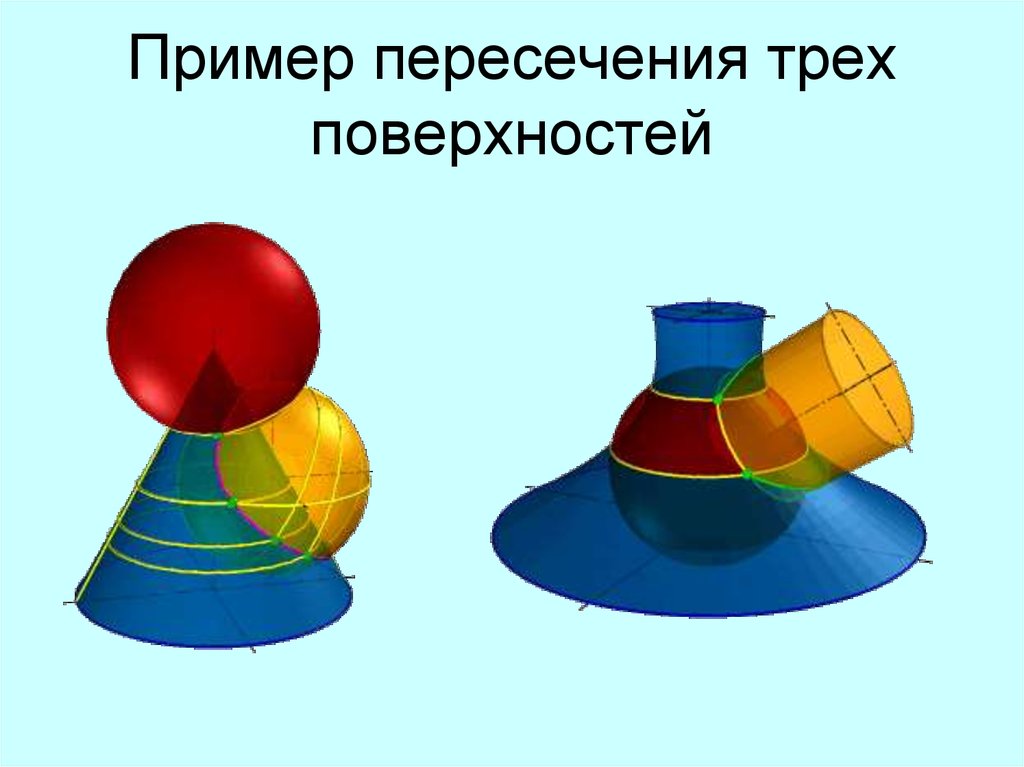
17.
Пример пересечения трехповерхностей










 Математика
Математика








