Похожие презентации:
Пересечение поверхностей
1.
ПЕРЕСЕЧЕНИЕПОВЕРХНОСТЕЙ
2.
Способы построениялиний пересечения
поверхностей
Способ
вспомогательных
секущих плоскостей
Частный случай, когда одна
из пересекающихся
поверхностей
или сразу две занимают
проецирующее положение
Способ сфер
3. Алгоритм построения линии пересечения гранных поверхностей (одна из которых занимает проецирующее положение)
• установить, какие поверхности участвуют впересечении;
• выявить проецирующие;
• установить, имеется ли полное проницание, или
частичная врезка;
• сделать вывод, что при пересечении гранных
поверхностей линией пересечения будет замкнутая
ломаная;
• установить, на какой(их) из плоскостей проекций есть
линия пересечения поверхностей;
• найти проекции точек пересечения ребер первого
многогранника с гранями второго и ребер второго
многогранника с гранями первого;
• проекции полученных точек последовательно
соединить отрезками с учетом видимости;
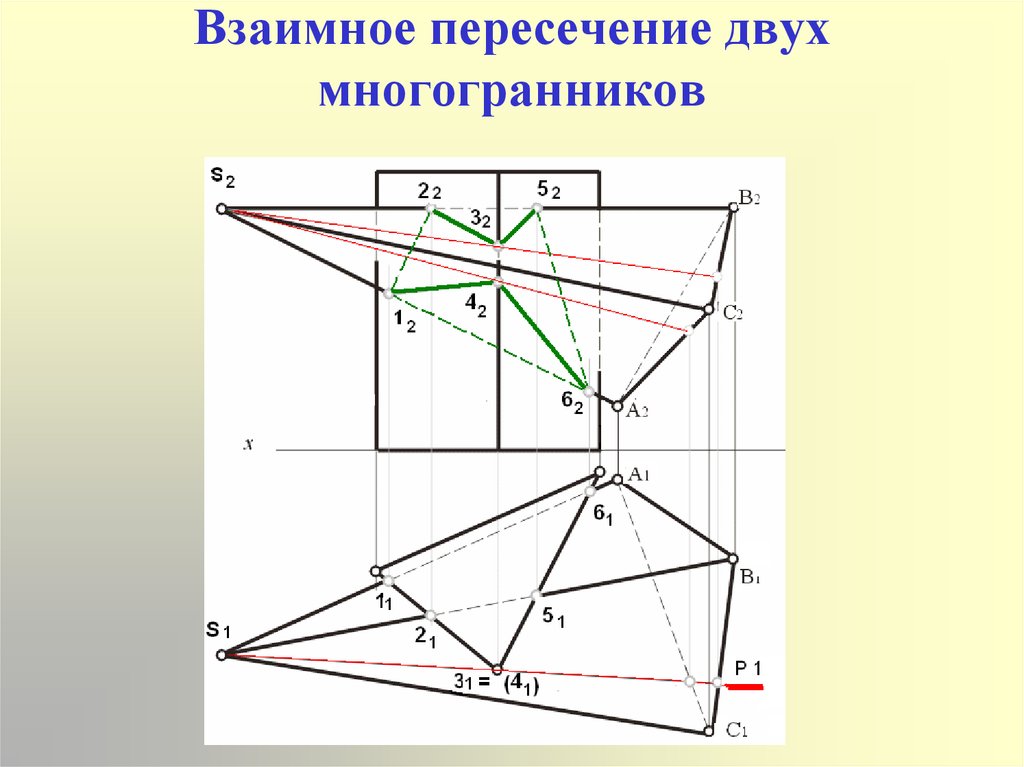
4. Взаимное пересечение двух многогранников
5. Пересечение гранных поверхностей
62S2
42
12
72
А2
52
В2
51
А1
С2
22 32
41
61
31
S1
71
11
В1
С1
21
6.
Пересечение гранных поверхностей,занимающих проецирующее положение
(43)
12
22
72
32
42
13
62
52
11
21=(71)
33
(53)
41=(51)
31=(61)
23
73
63
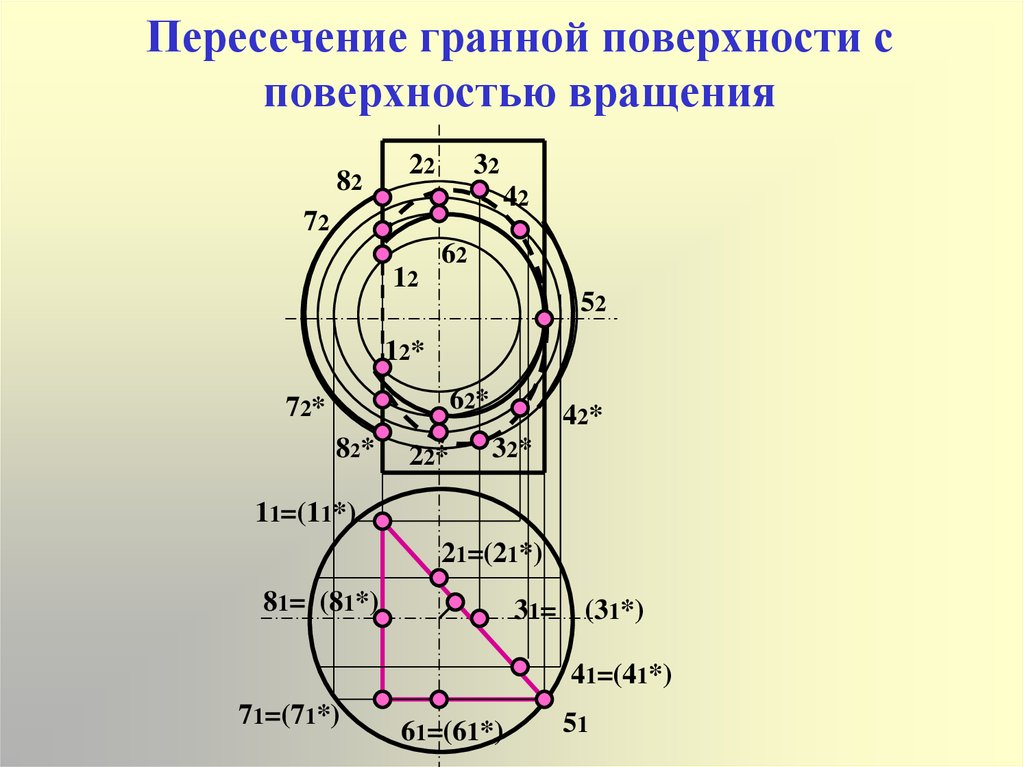
7. Пересечение гранной поверхности с поверхностью вращения
8222
32
42
72
12
62
52
12*
62*
72*
82 *
22*
42*
32*
11=(11*)
21=(21*)
81= (81*)
31= (31*)
41=(41*)
71=(71*)
61=(61*)
51
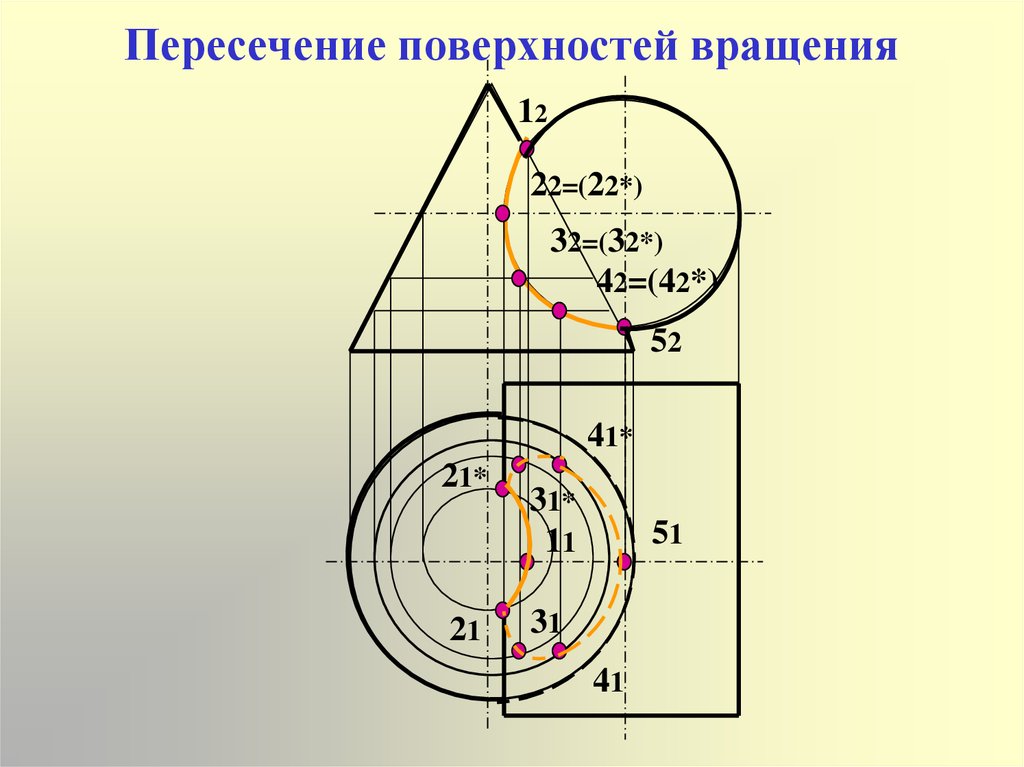
8. Пересечение поверхностей вращения
1222=(22*)
32=(32*)
42=(42*)
52
41*
21*
21
31*
11
51
31
41
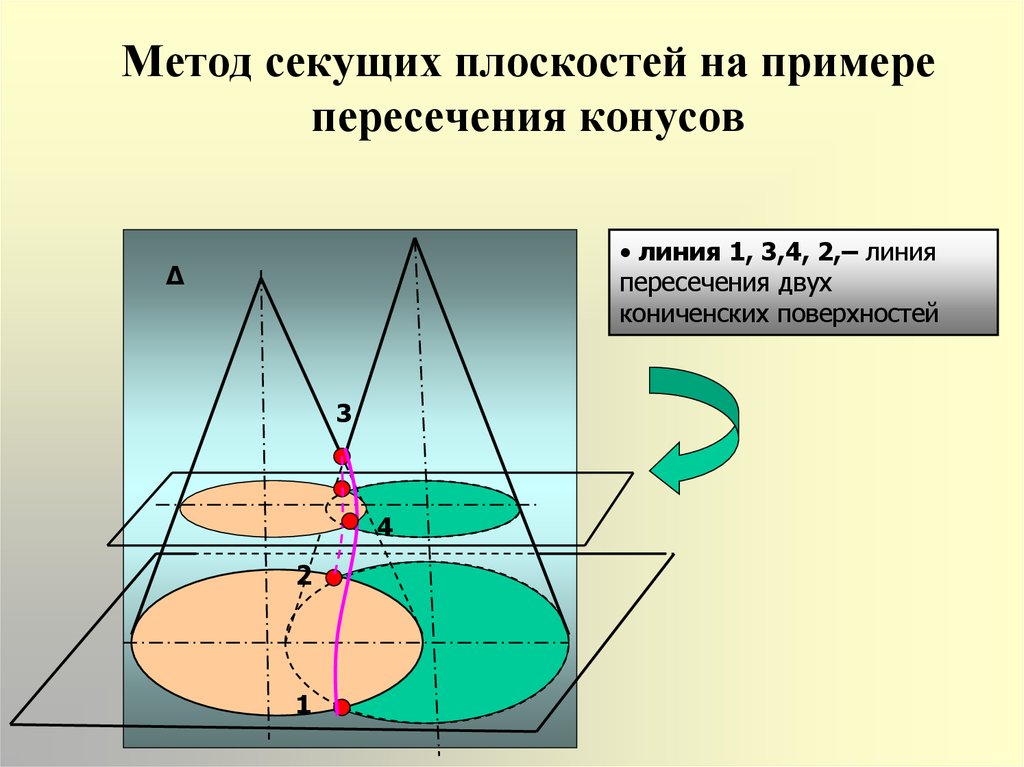
9. Метод секущих плоскостей на примере пересечения конусов
• линия 1, 3,4, 2,– линияпересечения двух
кониченских поверхностей
Δ
3
4
2
1
10. Построение линии пересечения двух конусов
i2i‘2
32
Θ2
42=(52)
Δ2
12=(22)
21
51
31
Σ1
41
11
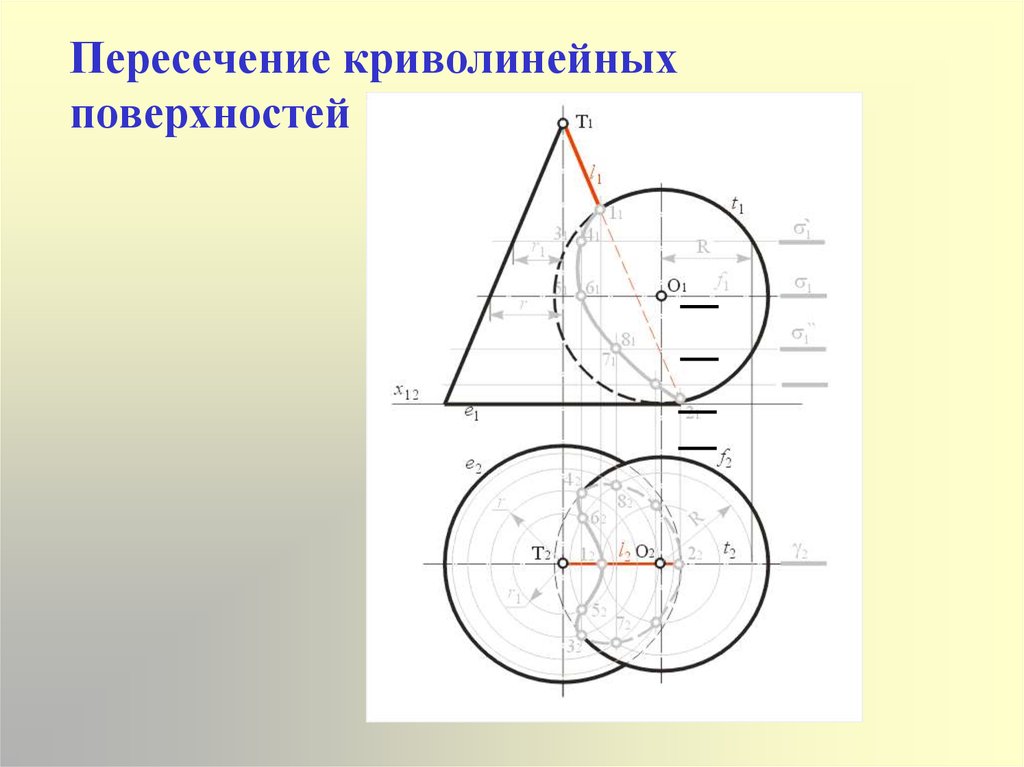
11. Пересечение криволинейных поверхностей
12. Метод вспомогательных секущих плоскостей
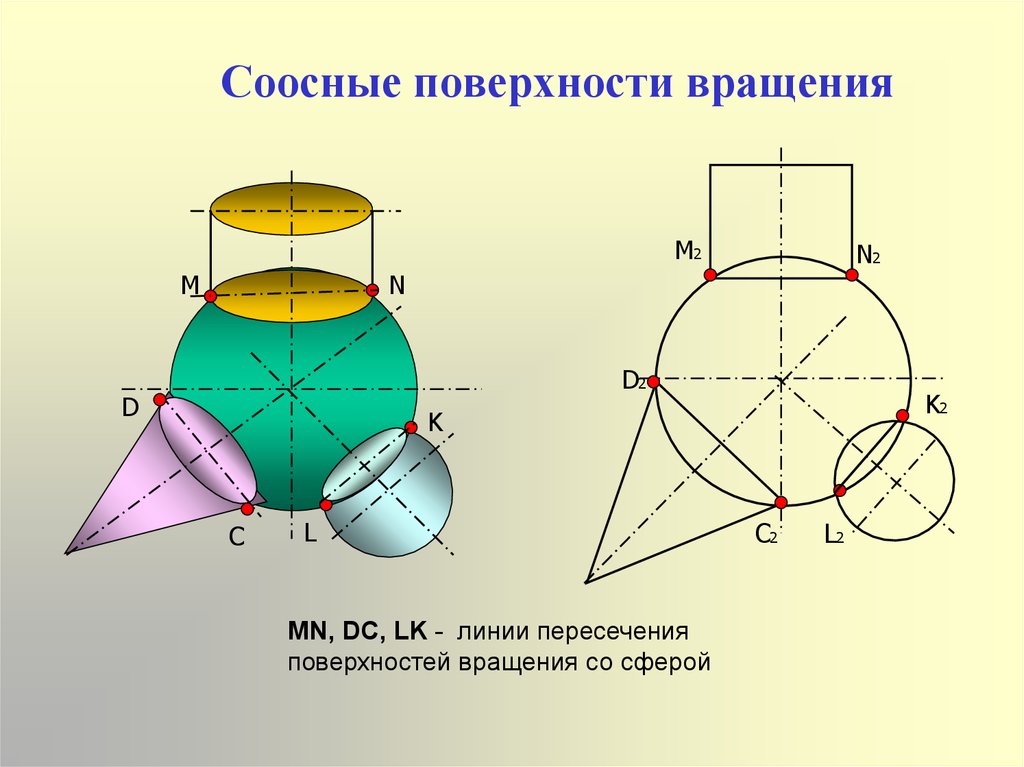
13. Соосные поверхности вращения
M2М
N2
N
D2
D
K2
K
С
L
MN, DC, LK - линии пересечения
поверхностей вращения со сферой
C2
L2
14.
• Соосными поверхностями вращенияназываются поверхности, имеющие
общую ось вращения.Эти поверхности
пересекаются по окружностям,
которые могут проецироваться в прямые
линии и строиться по точкам встречи
очерковых линий соосных поверхностей
вращения.
15. Метод секущих сфер
sS
12
22
72=(82)
52=(62)
42
32
61
(31)
21
51
81
11
(41)
71
16. Применение метода сфер
рисунок взят с сайта informatika.ru16
17. Теорема Монжа
Если две поверхности второго порядкаописаны вокруг третьей или вписаны в
неё, то линия пересечения распадается на
две плоские кривые второго порядка,
изображаемые на плоскости,
параллельной осям поверхностей в виде
прямолинейных отрезков.
18. Особые случаи пересечения поверхностей
9212
22=22*
82 = 82*
72 = 72*
32 =32*
62
52
81* 71*
31*
21 *
11
21
51
31
91
61
81 71












 Математика
Математика








