Похожие презентации:
Определенный интеграл
1.
Определённыйинтеграл
2.
Совокупность всех первообразных даннойфункции f(x) называется ее неопределенным
интегралом и обозначается f ( x)dx
Функция F(x) называется первообразной для
функции f(x) на данном промежутке, если для
любого x из этого промежутка F'(x) = f(x).
cf ( x)dx c f ( x)dx, c const
( f ( x) g ( x))dx f ( x)dx g ( x)dx
1
f (ax b)dx a F (ax b) C , a 0
3.
Определённый интегралОпределённый интеграл имеет большое
практическое применение. С его помощью
можно вычислять объёмы и площади
поверхностей геометрических тел, длину
кривой линии, площади плоских фигур,
важные физические величины (работу, силу,
теплоту и др.).
4.
Задачи, приводящие к понятиюопределенного интеграла
1.О вычислении площади криволинейной
трапеции
2.О вычислении массы стержня
3.О перемещении точки
5.
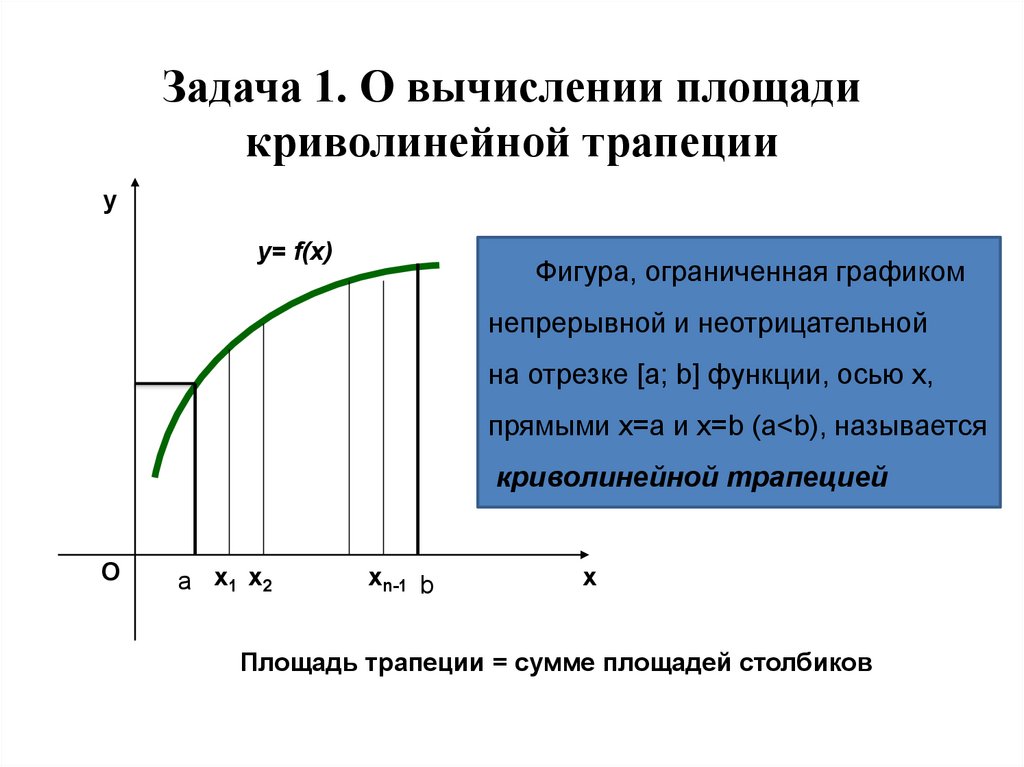
Задача 1. О вычислении площадикриволинейной трапеции
у
y= f(x)
Фигура, ограниченная графиком
непрерывной и неотрицательной
на отрезке [a; b] функции, осью х,
прямыми х=а и х=b (a<b), называется
криволинейной трапецией
О
а х1 х2
xn-1 b
х
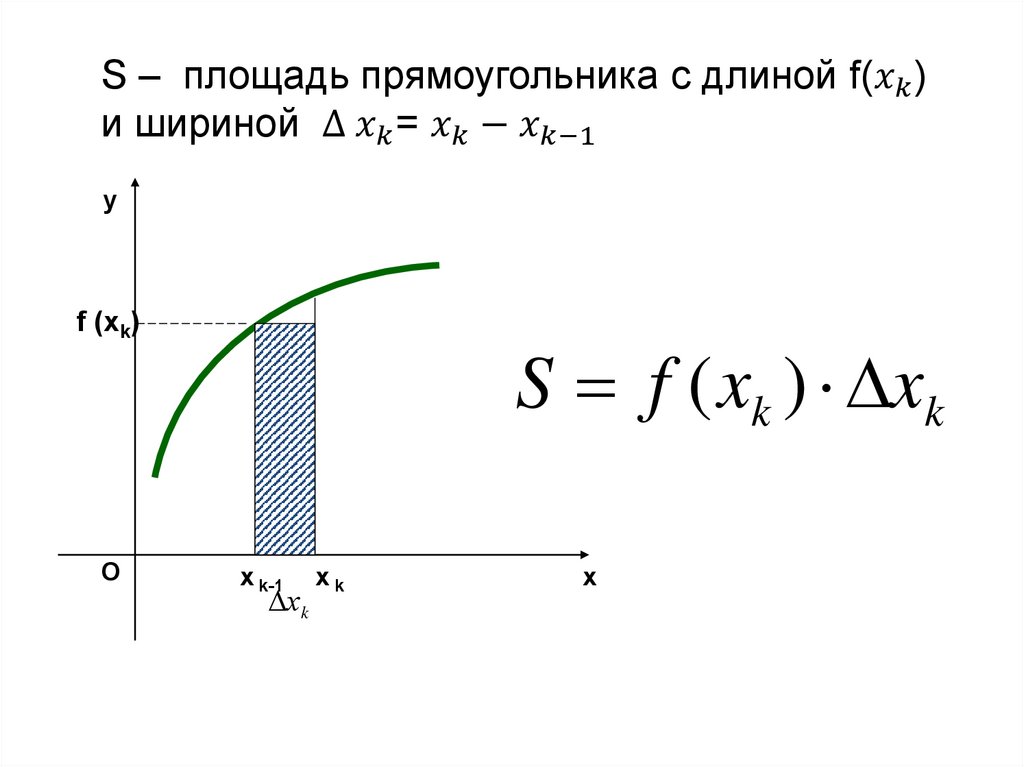
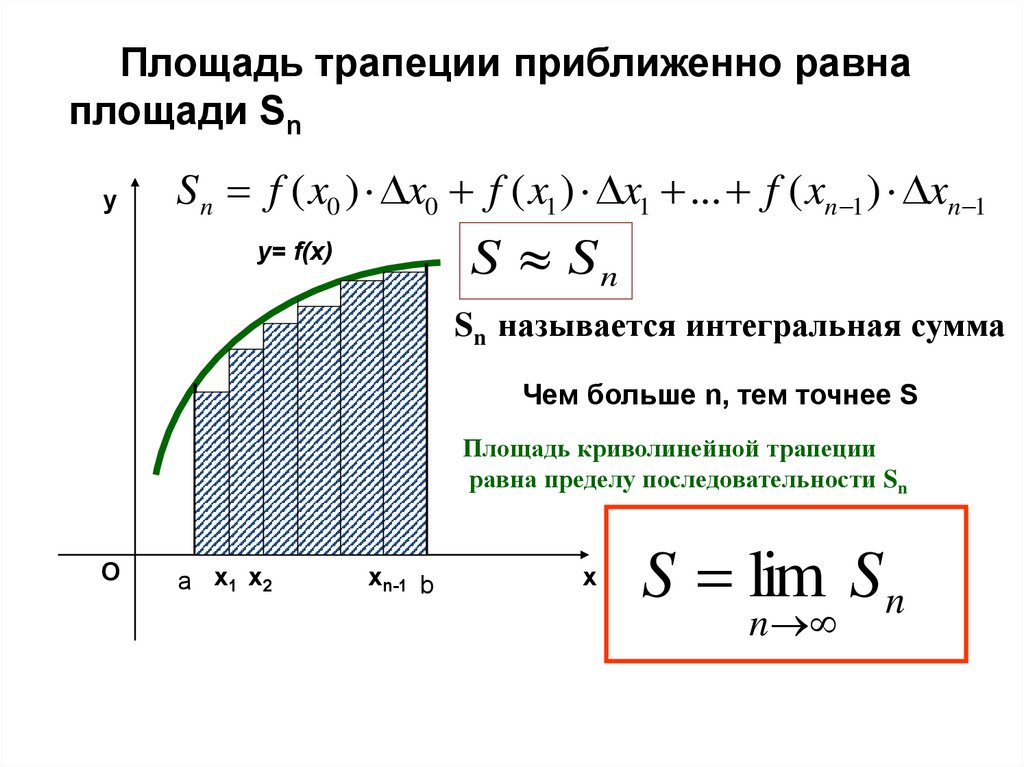
Площадь трапеции = сумме площадей столбиков











 Математика
Математика








