Решение уравнений с использованием формул двойного аргумента и формул понижения степени

1. Решение уравнений с использованием формул двойного аргумента и формул понижения степени

2.

Формулы двойного аргумента

3.

ФОРМУЛЫ ДВОЙНОГО АРГУМЕНТА
sin 2x 2 sin x cos x
2 sin x cos x sin 2x
cos 2 x cos 2 x sin 2 x
cos 2 x sin 2 x cos 2 x
cos 2 x 1 2 sin 2 x
1 2 sin 2 x cos 2 x
cos 2 x 2 cos x 1
2 cos 2 x 1 cos 2 x
2
tg 2 x
2tgx
1 tg 2 x
2tgx
tg 2 x
2
1 tg x

4.

sin 2 x cos x
2
Решите уравнение:
cos 2x cos x
Для функции в левой части уравнения
применим формулы приведения
2 cos 2 x 1 cos x
Применим формулу косинуса двойного
аргумента cos 2 x 2 cos 2 x 1
2 cos 2 x cos x 1 0
Перенесем cosx в левую часть уравнения.
изменив его знак на противоположный
Пусть
Решим полученное уравнение методом
введения новой переменной
t 1;1
cos x t
2t 2 t 1 0
t2
t1 1
1
2
Согласно замене
cos x 1
cos x
2
2 n, n Z
3
x 2 n, n Z
x
2 n,
2
2 n, n Z
3
Ответ:
1
2

5.

Решите уравнение:
3
cos
2 x cos x
2
sin 2x cos x
Для функции в левой части уравнения
применим формулы приведения
2 sin x cos x cos x
Применим формулу синуса двойного аргумента
sin 2x 2 sin x cos x
2 sin x cos x cos x 0
Перенесем cosx в левую часть уравнения.
изменив его знак на противоположный
cos x(2 sin x 1) 0
Решим полученное уравнение, разложив левую
часть на множители
произведение равно нулю тогда и только тогда,
когда один из множителей равен нулю, а другой
имеет смысл
cos x 0
x n, n Z
2
Ответ:
2
n,
6
2 n,
или
2 sin x 1 0
2 sin x 1
1
sin x
2
x1 2 n, n Z
6
5
x2
2 n, n Z
6
5
2 n, n Z
6

6.

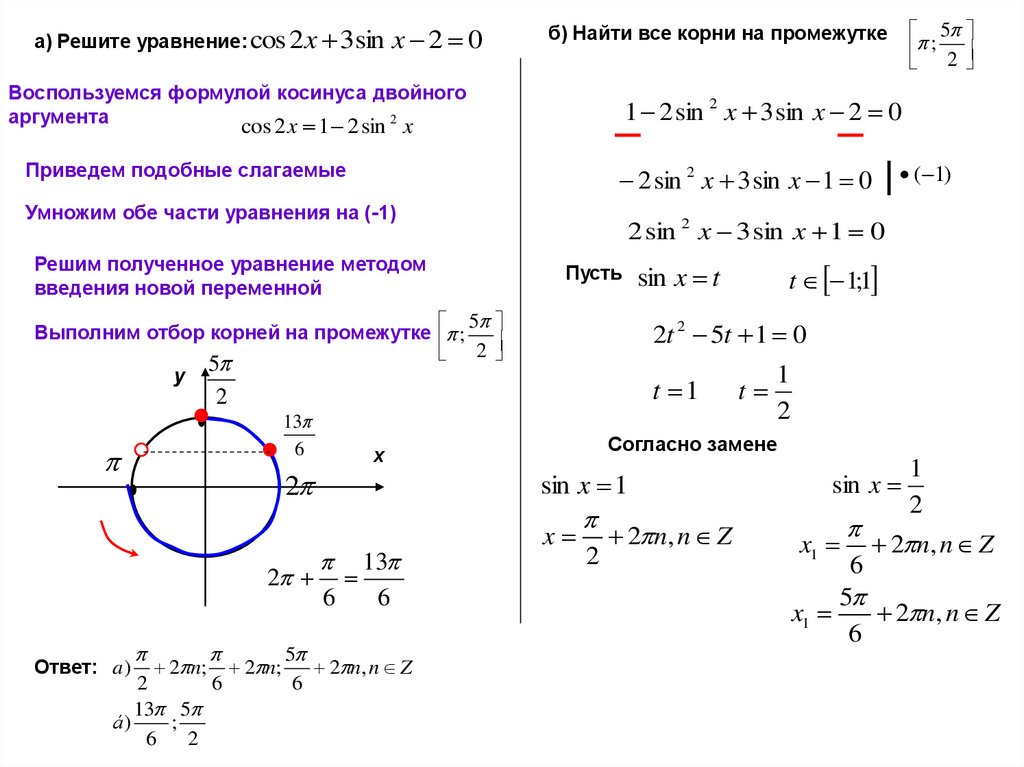
а) Решите уравнение: cos 2 x 3sin
x 2 0
Воспользуемся формулой косинуса двойного
аргумента
cos 2 x 1 2 sin 2 x
Приведем подобные слагаемые
1 2 sin 2 x 3 sin x 2 0
2 sin 2 x 3 sin x 1 0
Умножим обе части уравнения на (-1)
Решим полученное уравнение методом
введения новой переменной
5
Выполним отбор корней на промежутке ;
2
5
у
2
13
6
х
2
13
2
6
6
Ответ: a )
2 n;
2
6
13 5
á)
;
6
2
2 n;
5
2 n, n Z
6
5
; 2
б) Найти все корни на промежутке
( 1)
2 sin 2 x 3 sin x 1 0
Пусть
t 1;1
sin x t
2t 2 5t 1 0
t 1
t
1
2
Согласно замене
sin x 1
x 2 n, n Z
2
sin x
1
2
2 n, n Z
6
5
x1
2 n, n Z
6
x1

7.

Формулы понижения степени

8.

Формулы понижения степени ( они же формулы половинного аргумента)
cos 2 x 1
2
cos x
2
1 cos 2 x
cos 2 x
2
x 1 cos x
2
2
1 cos x
x
cos 2
2
2
1 cos 2 x
sin x
2
1 cos 2 x
sin 2 x
2
x 1 cos x
sin
2
2
1 cos x
x
sin
2
2
x 1 cos x
2 1 cos x
1 cos x
x
tg 2
1 cos x
2
cos 2
2
2
tg 2
2

9.

Решить уравнение:
Воспользуемся формулой
sin 2 x
sin 2 3 x
3
4
1 cos 6 x 3
2
4
1 cos 2 x
2
4(1 cos 6 x) 6
Можно использовать основное свойство
пропорции
:4
a c
a d c b
b d
1 cos 6 x 1,5
Разделим обе части уравнения на 4
cos 6 x 1,5 1
Слагаемое 1 перенесем в правую часть
равенства, изменив знак на
противоположный
cos 6 x 0,5
cos 6 x
Решаем простейшее тригонометрическое
уравнение
6x
x
Ответ:
9
( 1)
1
2
2
2 n, n Z
3
9
n
3
n
3
,n Z
,n Z
:6

10.

Решить уравнение
4 cos 4 x 4 cos 2 x 1 0 Найти все корни, принадлежащие промежутку 2 ;
Перепишем уравнение и применим формулу
понижения степени
2
4 cos 2 x 4 cos 2 x 1 0
2
Выполним возведение в степень
1 cos 2 x
1 cos 2 x
4
4
1 0
2
2
1 2 cos 2 x cos 2 2 x
1 cos 2 x
4
4
1 0
4
2
2
4 (1 2 cos 2 x cos 2 2 x) 4 (1 cos 2 x)
1 0
4
2
Каждую дробь можно сократить
Раскроем скобки и приведем подобные
слагаемые
Можно применить формулу понижения
степени еще раз
1 2 cos 2 x cos 2 2 x 2 2 cos 2 x 1 0
cos 2 2 x 0
1 cos 4 x
0
2
cos 4x 1
2
4 x 2 n, n Z
x
4
n
2
,n Z
:4

11.

Найдем все корни, принадлежащие промежутку 2 ;
В этом случае отбор корней удобнее выполнить с помощью двойного неравенства
2
9
4
2
4
4
n
4
2
n
2
4
9 n
5
4
2
4
4,5 n 2,5
n 4; x
n Z
n 3; x
Ответ:
4
n
2
4
4
4
, n Z;
2
3
2
4
4
7
5
;
.
4
4
8
7
4
4
6
5
4
4
4
4
2
5
4