Формулы половинного угла. Формулы понижения степени

1. Формулы половинного угла. Формулы понижения степени

2.

Повторение
Установите истинность или ложность утверждений:
1
1 2 sin 2 x 2 cos x
2 cos 2 x sin 2 x cos 2 x
неверно
1 2 sin 2 x cos 2 x
верно
2tgx
1 tg 2 x
4 cos 2 x 1 cos 2 x
неверно
2 cos 2 x 1 cos 2 x
5 sin 2x sin x cos x
неверно
sin 2x 2 sin x cos x
6 1 2 sin 2 x cos 2 x
верно
3 tg 2 x
7 cos x sin x cos 2 x
2
2
верно
неверно
8 cos 2 x 2 cos 2 x 1
верно
x
x
9 sin x 2 sin cos
2
2
верно
cos 2 x sin 2 x cos 2 x

3.

1. Примените формулы двойного аргумента к следующим выражениям:
sin 80 0 2 sin 400 cos 400
7
7
2 7
2 7
cos
sin
cos 2
cos
6
12
12
12
tg8 2tg 4
1 tg 2 4
2. Упростите выражение, а затем вычислите:
cos 2 22,50 sin 2 22,50 cos 2 22,50 cos 450
2
2
3
0
0
0
0
0
2 sin 15 cos 15 sin 2 15 sin 2 30 cos 30 2
4
4
4

4.

Формулы понижения степени
Рассмотрим формулу косинуса двойного аргумента
Слагаемое ( -1) перенесем в правую часть
равенства, изменив знак на
противоположный
Разделим обе части равенства на 2
Получаем первую формулу
2 cos 2 x cos 2 x 1
cos 2 x 1
cos x
2
2
Рассмотрим формулу косинуса двойного аргумента
Слагаемое ( -1) перенесем в правую часть
равенства, изменив знак на
противоположный
Разделим обе части равенства на - 2
1 2 sin 2 x cos 2 x
2 sin 2 x cos 2 x 1
1 cos 2 x
sin x
2
2
Получаем вторую формулу
2 cos 2 x 1 cos 2 x

5.

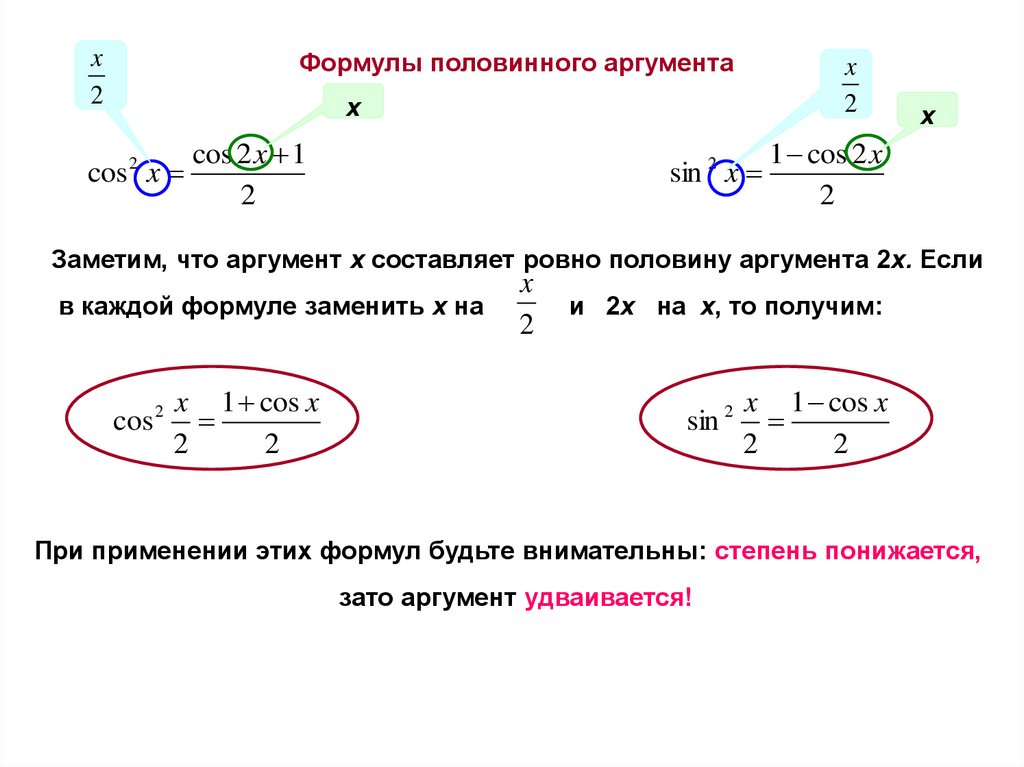
Формулы половинного аргумента
x
2
х
cos 2 x 1
cos x
2
x
2
х
1 cos 2 x
sin x
2
2
2
Заметим, что аргумент х составляет ровно половину аргумента 2х. Если
в каждой формуле заменить х на
cos 2
x 1 cos x
2
2
x
2
и 2х на х, то получим:
sin 2
x 1 cos x
2
2
При применении этих формул будьте внимательны: степень понижается,
зато аргумент удваивается!

6.

Формула тангенса половинного аргумента
x
1 cos x
2 x
2
1 cos x
2
1 cos x
2
tg
x
2
1 cos x
2
1 cos x
1 cos x
cos 2
2
2
sin 2
tg 2
x 1 cos x
2 1 cos x

7.

Формулы понижения степени ( они же формулы половинного аргумента)
cos 2 x 1
2
cos x
2
1 cos 2 x
cos 2 x
2
x 1 cos x
2
2
1 cos x
x
cos 2
2
2
1 cos 2 x
sin x
2
1 cos 2 x
sin 2 x
2
x 1 cos x
sin
2
2
1 cos x
x
sin
2
2
x 1 cos x
2 1 cos x
1 cos x
x
tg 2
1 cos x
2
cos 2
2
2
tg 2
2

8.

№ 27.19 б) Вычислить с помощью формул половинного аргумента
Воспользуемся формулой
Сначала найдем
Найдем значение
2
cos 2
x 1 cos x
2
2
0
cos 22,5
cos 450
Дробь запишем в виде суммы двух
дробей
Получаем
0
Чтобы найти cos 22,5 , нужно извлечь
квадратный корень из суммы
Заметим, что аргумент 22,5 является
углом первой координатной четверти,
поэтому косинус этого аргумента –
положительное число
cos 22,50
1 cos 2 22,50
cos 22,5
2
1 cos 450
2
0
cos 22,5
2
2
1
2
cos2 22,50
2
2
1
cos 2 22,50 2
2
2
1
2
cos 2 22,50
2 4
2
0
cos 22,50
Ответ:
1
2
2 4
cos 22,50
1
2
2 4

9.

Упростить выражение:
Воспользуемся формулой
x
2 sin
cos x
2
2
sin 2 x
Сократим дробь на 2
Приведем подобные слагаемые
Получаем
1 cos 2 x
2
x
1 cos x
2 sin
cos x 2
cos x
2
2
2
2 sin 2
x
2 (1 cos x)
cos x
cos x
2
2
2 sin 2
x
cos x 1 cos x cos x
2
2 sin 2
x
cos x 1
2
Ответ: 1

10.

Дано:
2
cos 2 x
3
Вычислить: sin 4 x cos 4 x
sin 2 x
1 cos 2 x
2
cos 2 x
sin x cos x
Представим каждое слагаемое в виде
квадрата
2
2
2
2
1 cos 2 x 1 cos 2 x
2
2
2
Воспользуемся формулами понижения
степени
1 cos 2 x
2
2
Возведем в квадрат числитель и
знаменатель каждой дроби
Обратите внимание, что при возведении
в квадрат числителей, нужно
использовать формулу квадрата
разности и формулу квадрата суммы
соответственно
1 2 cos 2 x cos 2 2 x 1 2 cos 2 x cos 2 2 x
4
4
a b 2 a 2 2ab b 2 a b 2 a 2 2ab b 2
1 2 cos 2 x cos 2 2 x 1 2 cos 2 x cos 2 2 x
4
Найдем сумму дробей с одинаковыми
знаменателями и упростим числитель
Воспользуемся начальным условием cos 2 x
2 2 cos 2 2 x
4
2
3
2
4
26
2
2 2
2 2
13
9 9
3
18
4
4
4
13
Ответ:
18