Позиционные задачи

1. Позиционные задачи

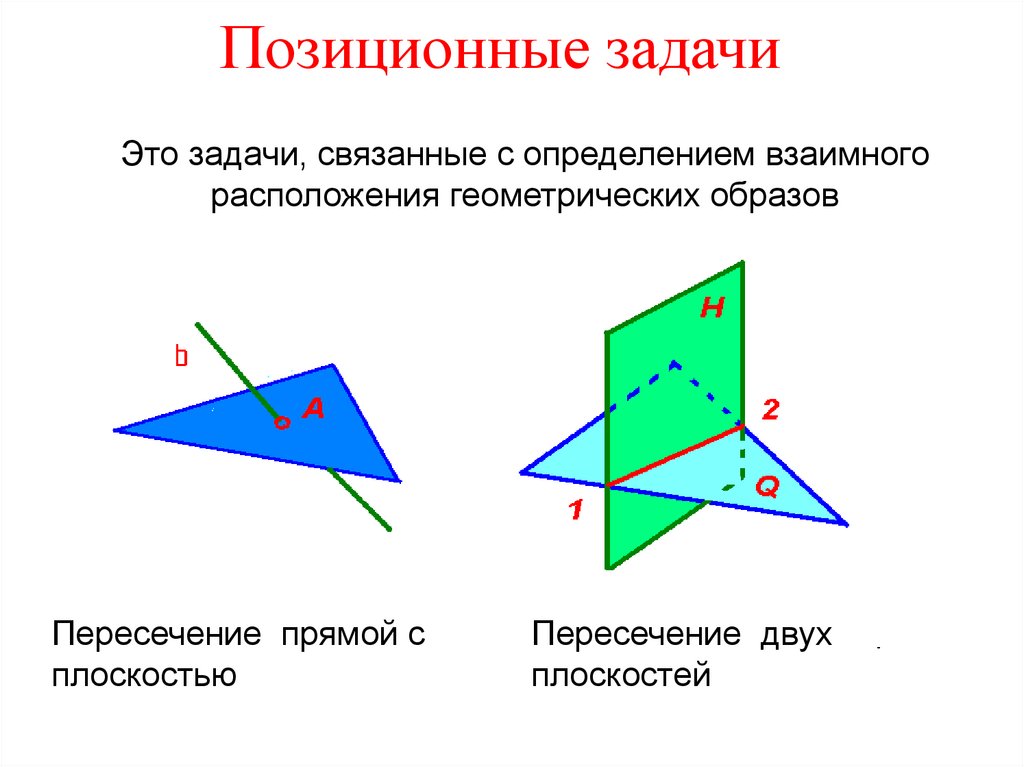
Это задачи, связанные с определением взаимного
расположения геометрических образов
Пересечение прямой с
плоскостью
Пересечение двух
плоскостей

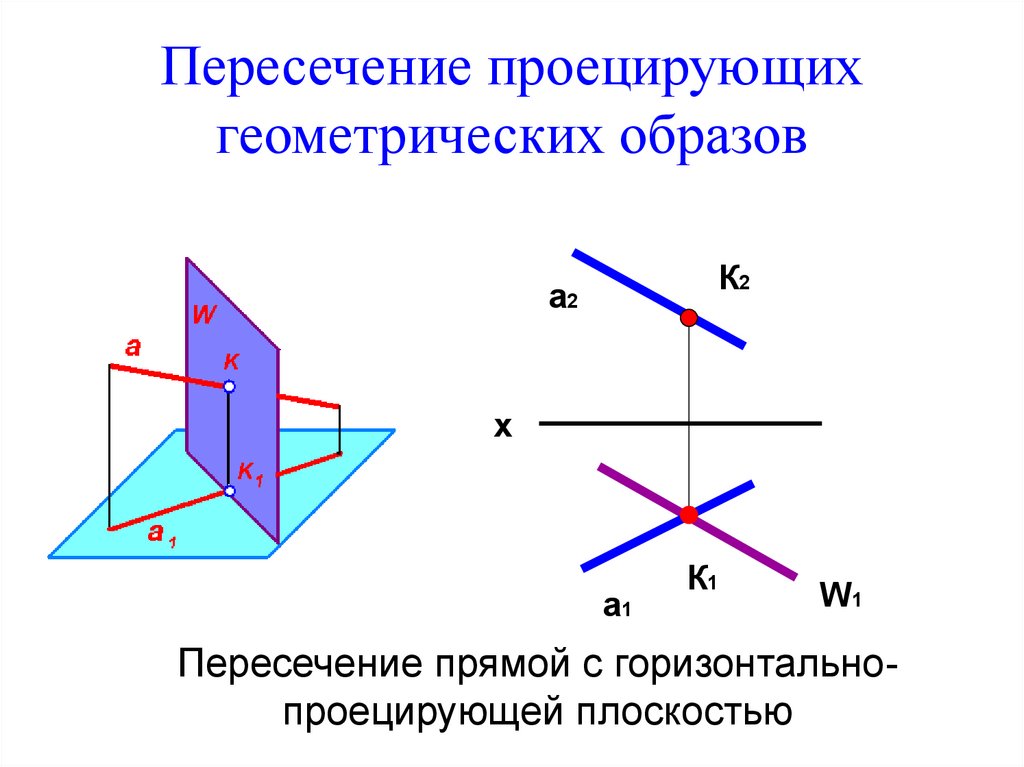
2. Пересечение проецирующих геометрических образов

К2
а2
х
а1
К1
W1
Пересечение прямой с горизонтальнопроецирующей плоскостью

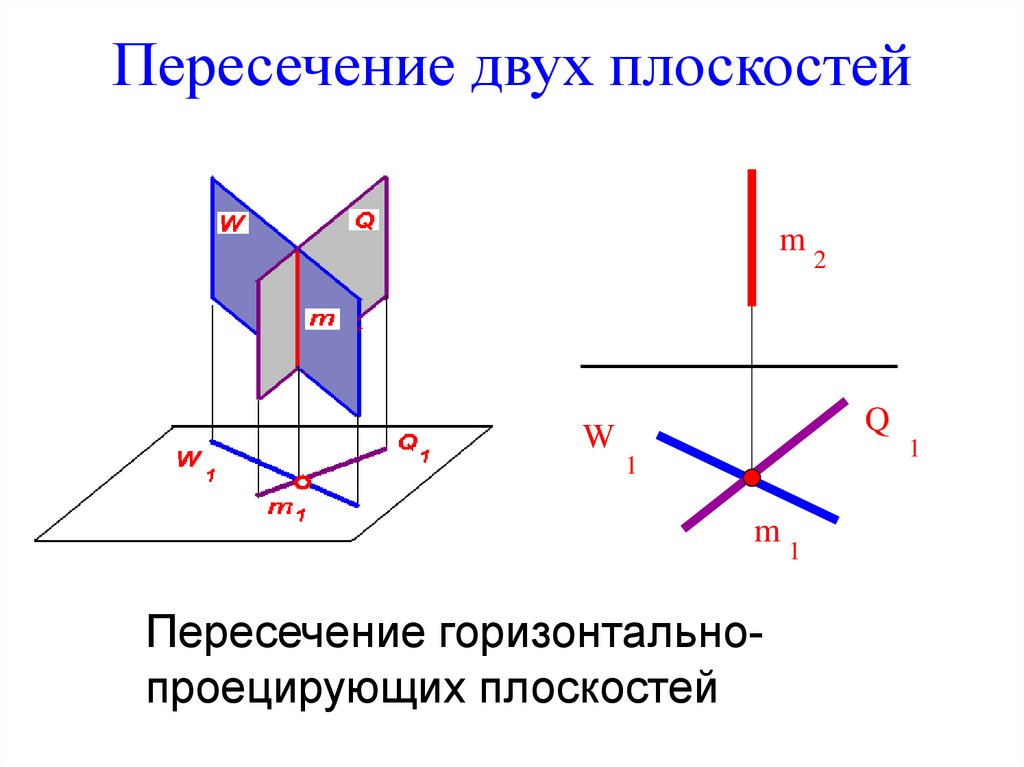
3. Пересечение двух плоскостей

m
2
Q
W
1
1
m
Пересечение горизонтальнопроецирующих плоскостей
1

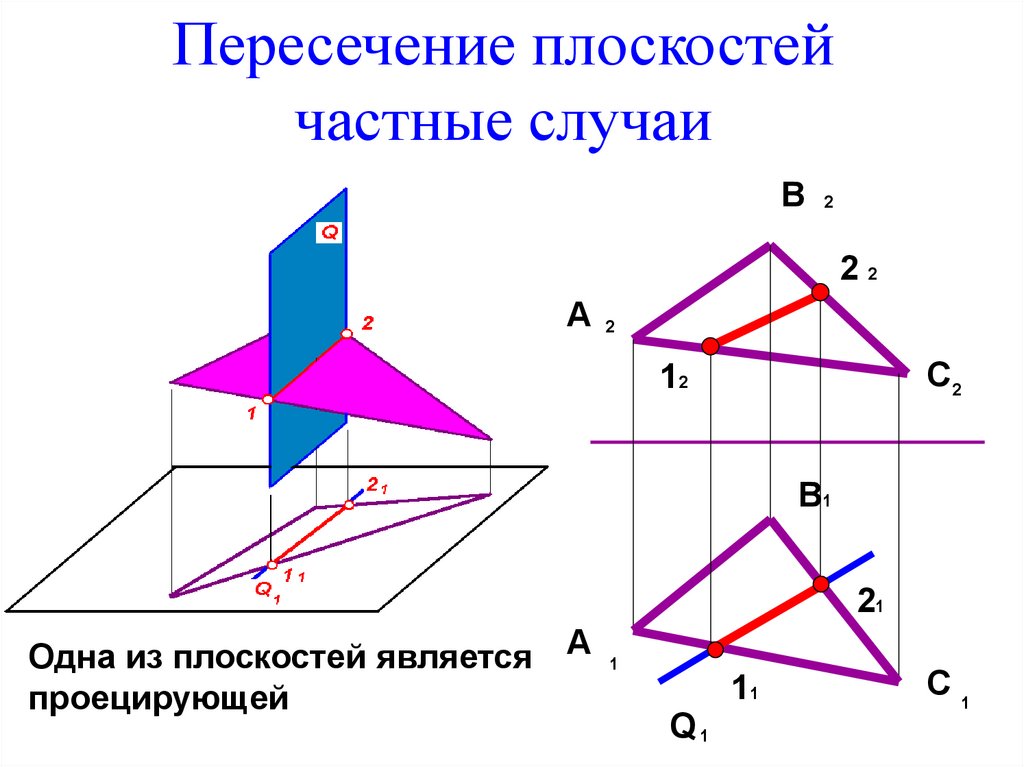
4. Пересечение плоскостей частные случаи

В 2
22
А 2
C2
12
В1
21
Одна из плоскостей является А 1
проецирующей
11
Q1
С1

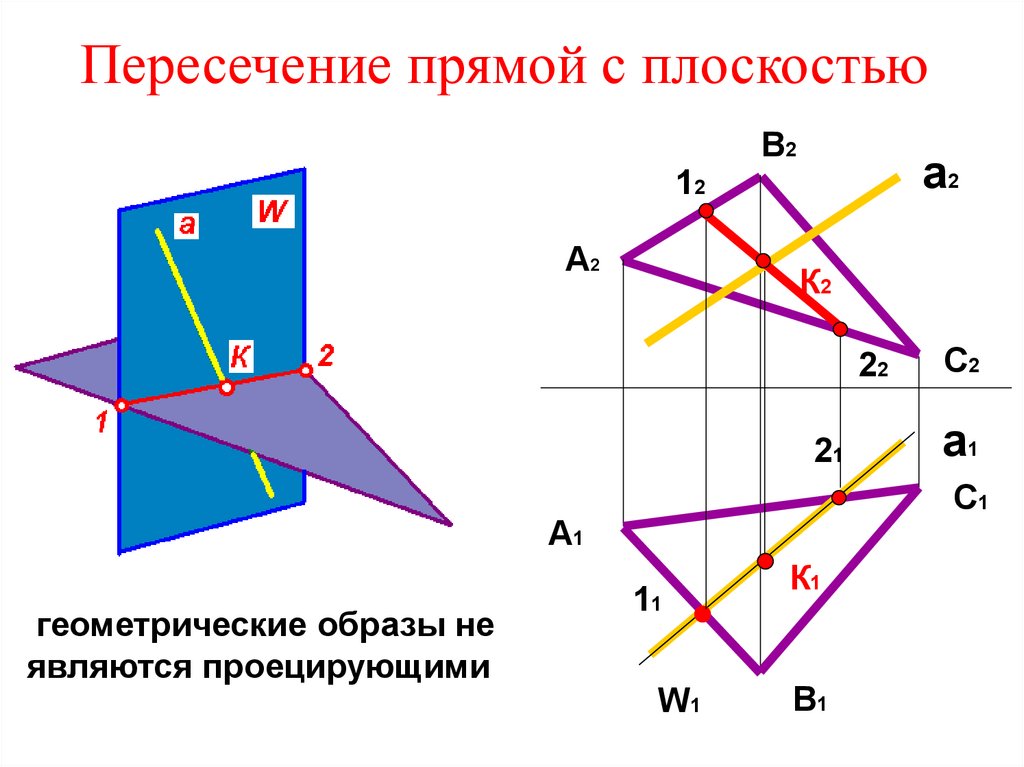
5. Пересечение прямой с плоскостью

В2
а2
12
А2
К2
22
21
а1
С1
А1
геометрические образы не
являются проецирующими
С2
11
W1
К1
В1

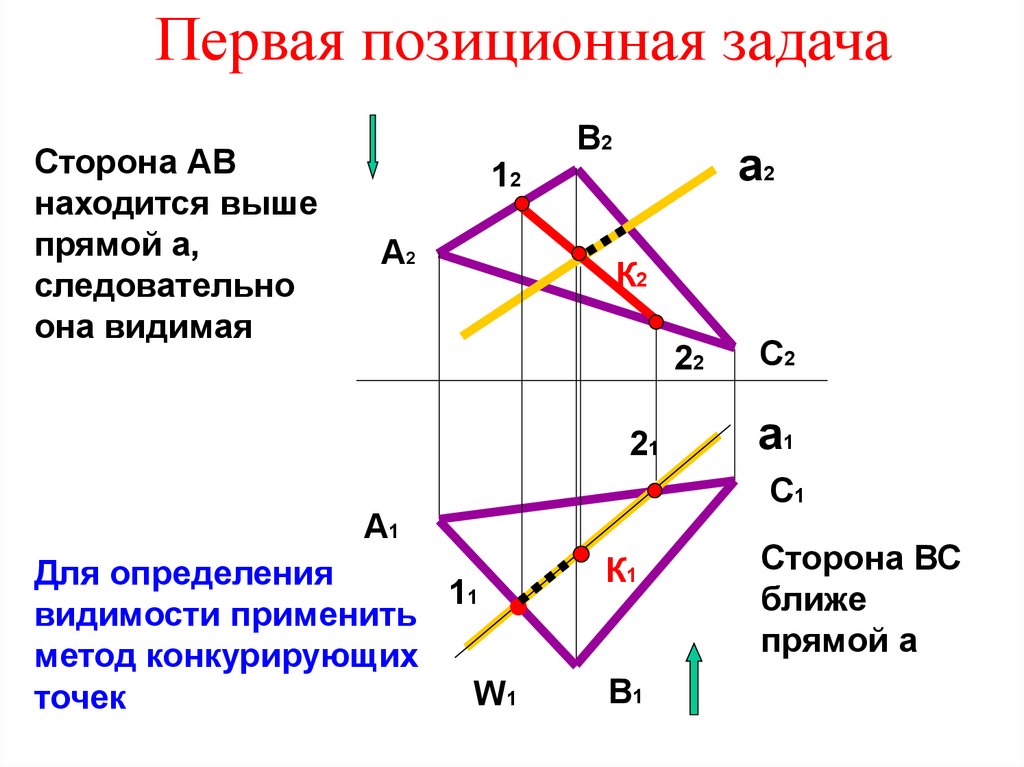
6. Первая позиционная задача

Сторона АВ
находится выше
прямой а,
следовательно
она видимая
В2
а2
12
А2
К2
22
21
а1
С1
А1
Для определения
11
видимости применить
метод конкурирующих
W1
точек
С2
К1
В1
Сторона ВС
ближе
прямой а

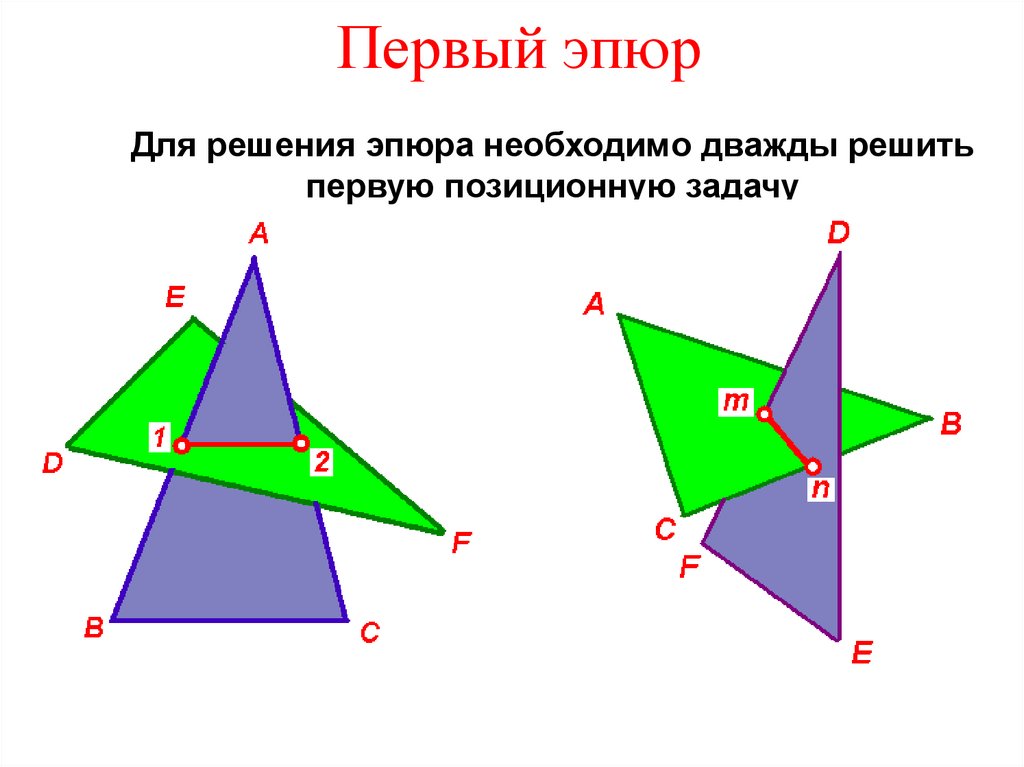
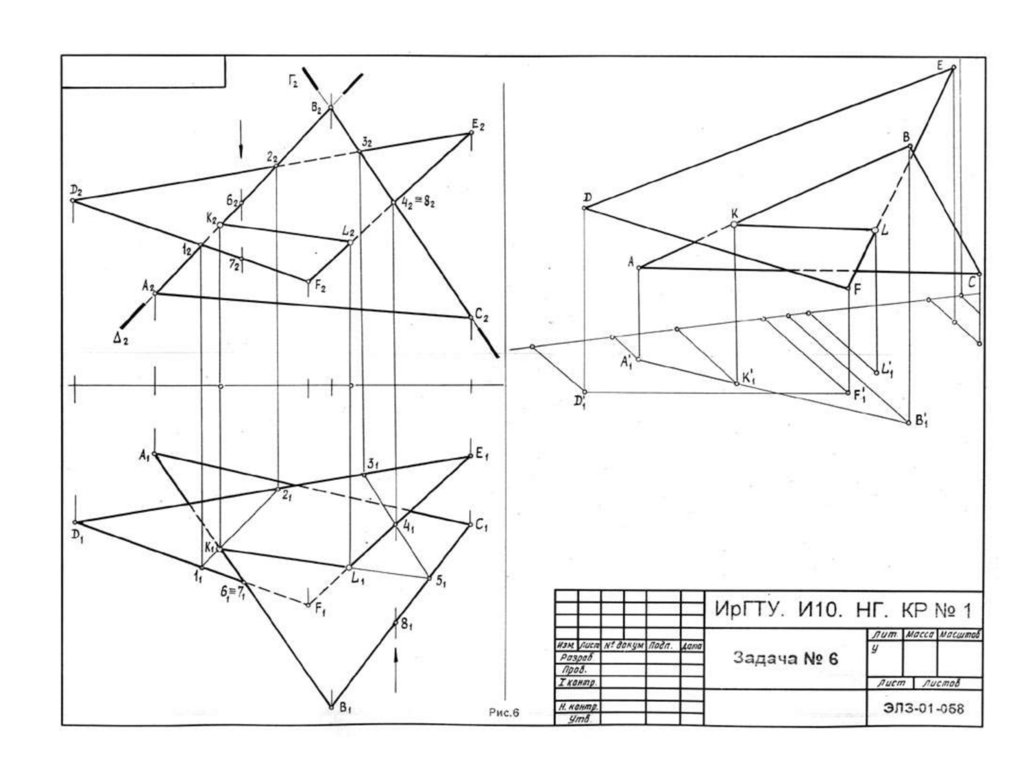
7. Первый эпюр

Для решения эпюра необходимо дважды решить
первую позиционную задачу

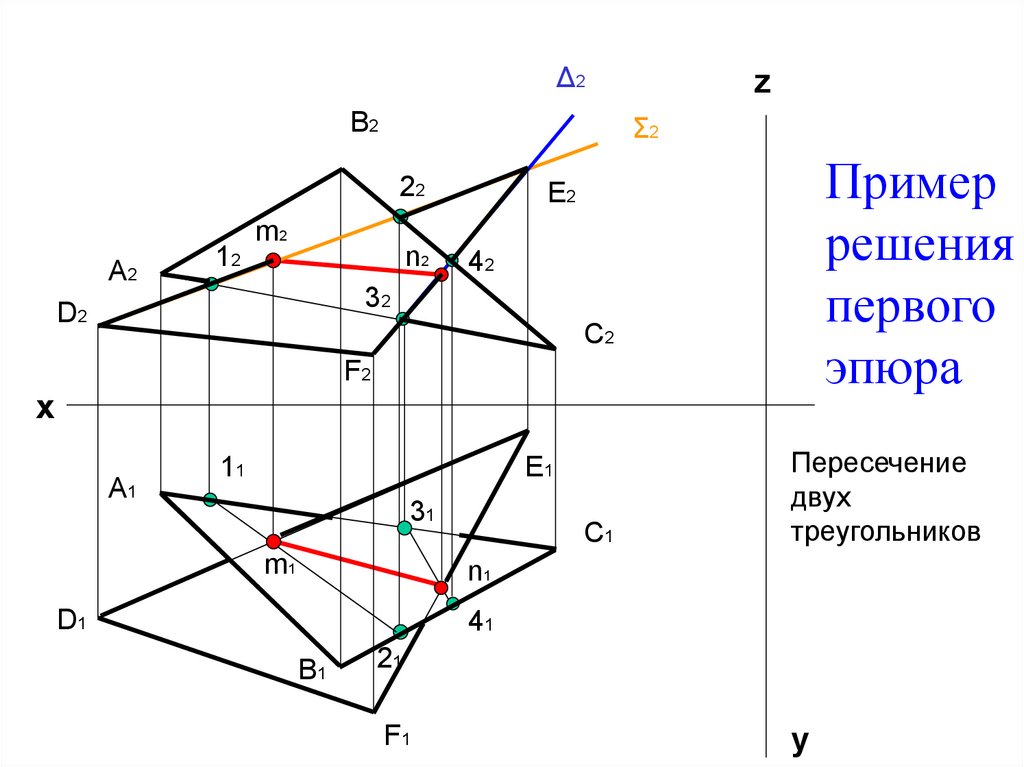
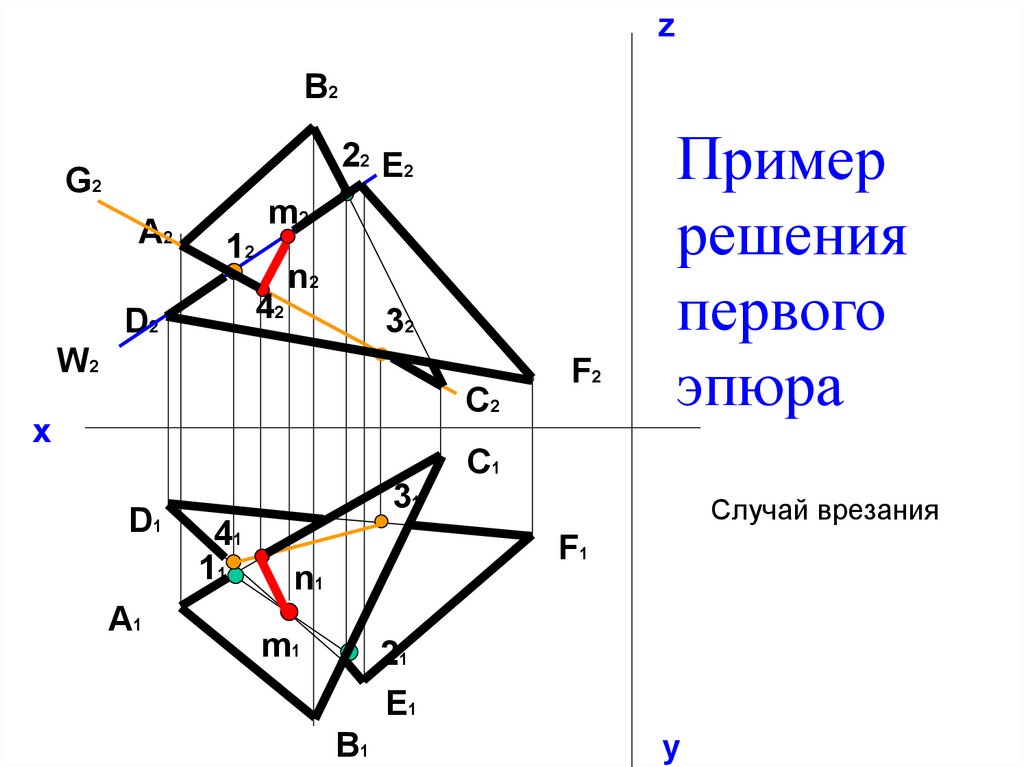
8. Пример решения первого эпюра

Δ2
B2
Σ2
22
A2
12
z
m2
n2
Пример
решения
первого
эпюра
E2
42
32
D2
C2
F2
х
A1
11
E1
31
m1
C1
Пересечение
двух
треугольников
n1
D1
41
B1
21
F1
y

9. Пример решения первого эпюра

z
B2
22 E2
G2
A2
m2
12
42
D2
n2
32
W2
C2
x
F2
Пример
решения
первого
эпюра
C1
D1
A1
31
41
11
Случай врезания
F1
n1
m1
21
E1
B1
y

10.

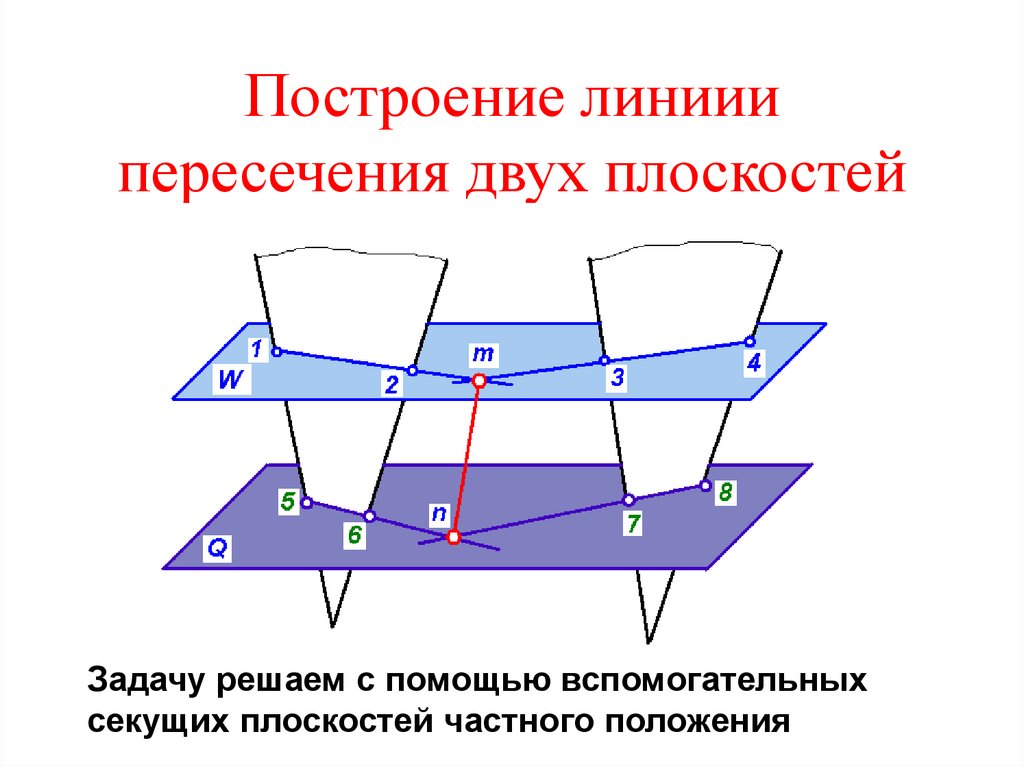
11. Построение линиии пересечения двух плоскостей

Задачу решаем с помощью вспомогательных
секущих плоскостей частного положения

12. Построение линии пересечения двух плоскостей

12
52
51
m2
22
62
n2
32
42
Q2
82
72
81
61
n1
71
11
21
31
m1
W2
41

13.

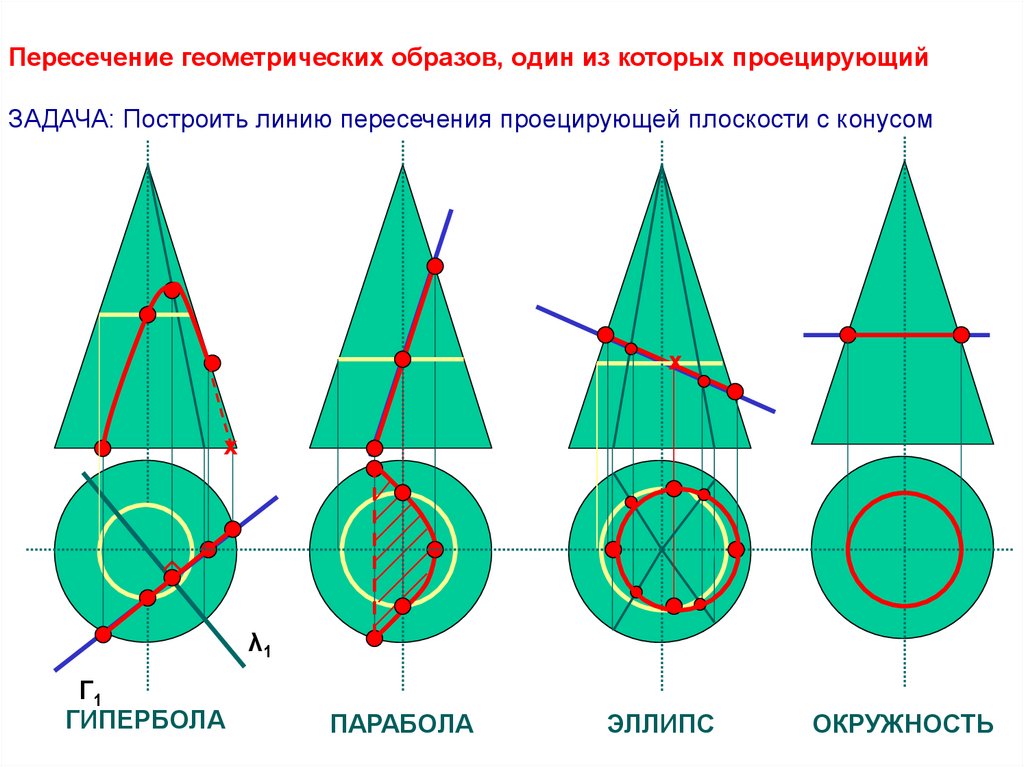
Пересечение геометрических образов, один из которых проецирующий
ЗАДАЧА: Построить линию пересечения проецирующей плоскости с конусом
х
х
λ1
Г1
ГИПЕРБОЛА
ПАРАБОЛА
ЭЛЛИПС
ОКРУЖНОСТЬ