Похожие презентации:
Решение задач с помощью систем линейных уравнений. №1102. №1104
1.
Решение задач с помощьюсистем линейных уравнений
2.
№1102Пусть 1 кг огурцов стоит х руб., а 1 кг помидоров стоит у руб.
Тогда 4 кг огурцов и 3 кг помидоров будут стоить (4х + 3у) руб.,
что по условию равно 240 руб., т.е. 4х + 3у = 240.
После того как огурцы подорожали на 50%, а помидоры
подешевели на 20%, то 1 кг огурцов будет стоить х + 0,5х=1,5х
руб., а 1 кг помидоров будет стоить (у – 0,2у)=0,8у руб. Тогда 2 кг
огурцов и 5 кг помидоров будут стоить (2∙1,5х +5∙0,8у)=(3х + 4у)
руб., что составляет 250 руб., т.е. 3х + 4у = 250.
Составим и решим систему уравнений.
4х + 3у = 240, ∙3
3х + 4у = 250, ∙(-4)
3х + 4у = 250,
12х + 9у = 720,
3х = 250 – 4∙40,
– 12х – 16у = –1000,
3х = 250 – 160,
– 7у = –280,
3х = 90,
у = 40.
х = 30.
Итак, 1 кг огурцов стоит 30 руб., а 1 кг помидоров стоит 40 руб.
Ответ: 30 руб., 40 руб.
3.
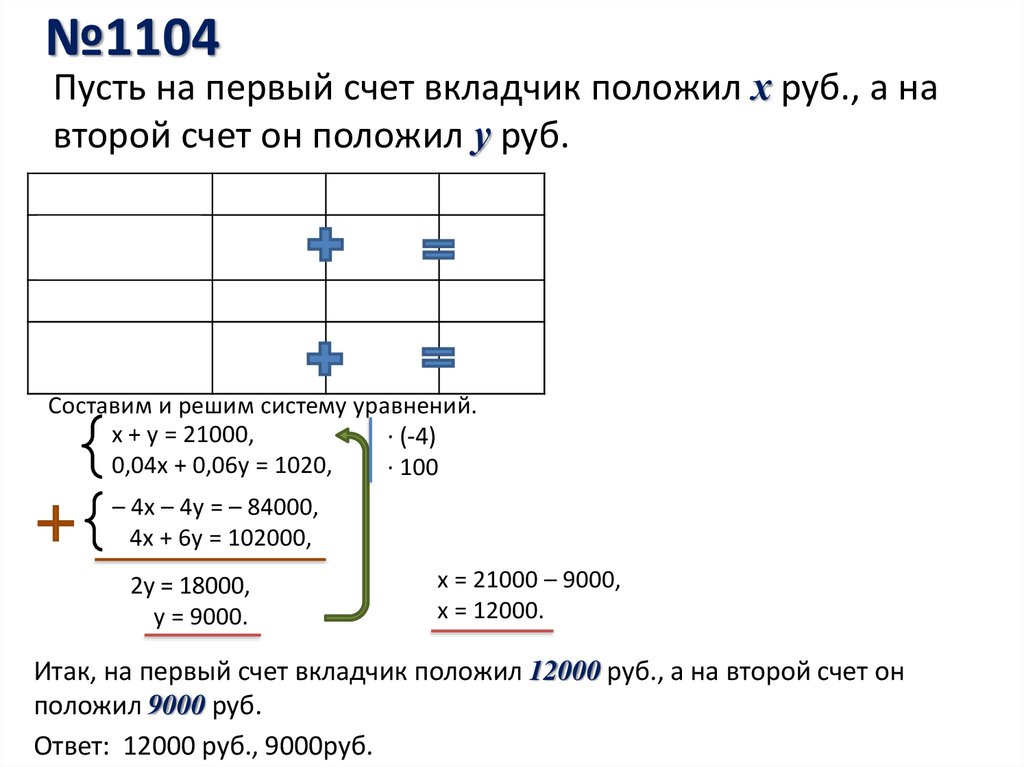
№1104Пусть на первый счет вкладчик положил х руб., а на
второй счет он положил у руб.
1 счет
2 счет
Всего
х
у
21000
Первоначальная
сумма, руб.
% годовых
4%=0,04 6%=0,06
Проценты по
0,04х
0,06у
1020
вкладу, руб.
Составим и решим систему уравнений.
х + у = 21000,
∙ (-4)
0,04х + 0,06у = 1020,
∙ 100
– 4х – 4у = – 84000,
4х + 6у = 102000,
2у = 18000,
у = 9000.
х = 21000 – 9000,
х = 12000.
Итак, на первый счет вкладчик положил 12000 руб., а на второй счет он
положил 9000 руб.
Ответ: 12000 руб., 9000руб.
4.
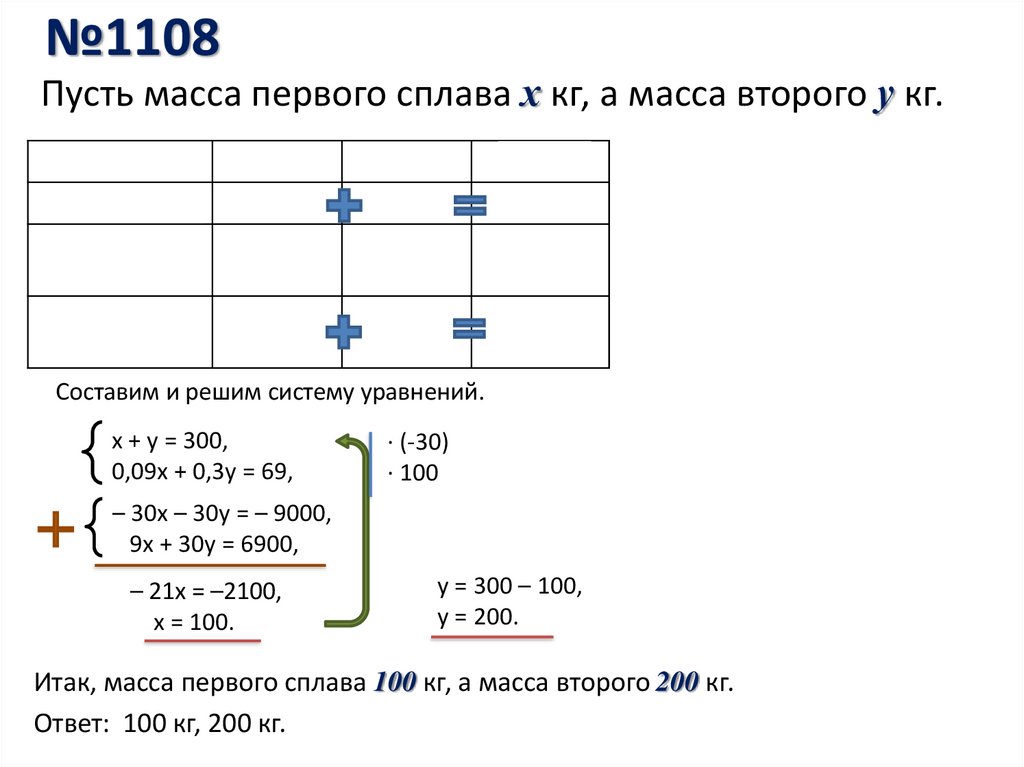
№1108Пусть масса первого сплава х кг, а масса второго у кг.
1 сплав
2 сплав
3 сплав
Масса сплава, кг
х
у
300
% содержания
цинка
9%=0,09
30%=0,3
23%=0,23
Масса цинка в
сплаве, кг
0,09х
0,3у
0,23∙300
Составим и решим систему уравнений.
х + у = 300,
0,09х + 0,3у = 69,
∙ (-30)
∙ 100
– 30х – 30у = – 9000,
9х + 30у = 6900,
– 21х = –2100,
х = 100.
у = 300 – 100,
у = 200.
Итак, масса первого сплава 100 кг, а масса второго 200 кг.
Ответ: 100 кг, 200 кг.
5.
№1110Пусть в данном числе х десятков и у единиц, т.е. ху = 10х + у.
Если поменять местами цифры, то получиться ух = 10у + х.
По условию 10у + х меньше 10х + у на 9, а так же х + у = 15.
Составим и решим систему уравнений.
х + у = 15,
10х + у – (10у + х) = 9,
х + у = 15,
10х + у – 10у – х = 9,
х + у = 15,
9х – 9у = 9,
х + у = 15,
х – у = 1,
2х = 16,
х = 8.
:9
у = 15 – х,
у = 15 – 8,
у = 7.
Ответ: данное число 87.
6.
Домашнее задание• №1105, 1109.




 Математика
Математика