Определённый интеграл. Урок 69

1. Определённый интеграл

Урок 69

2.

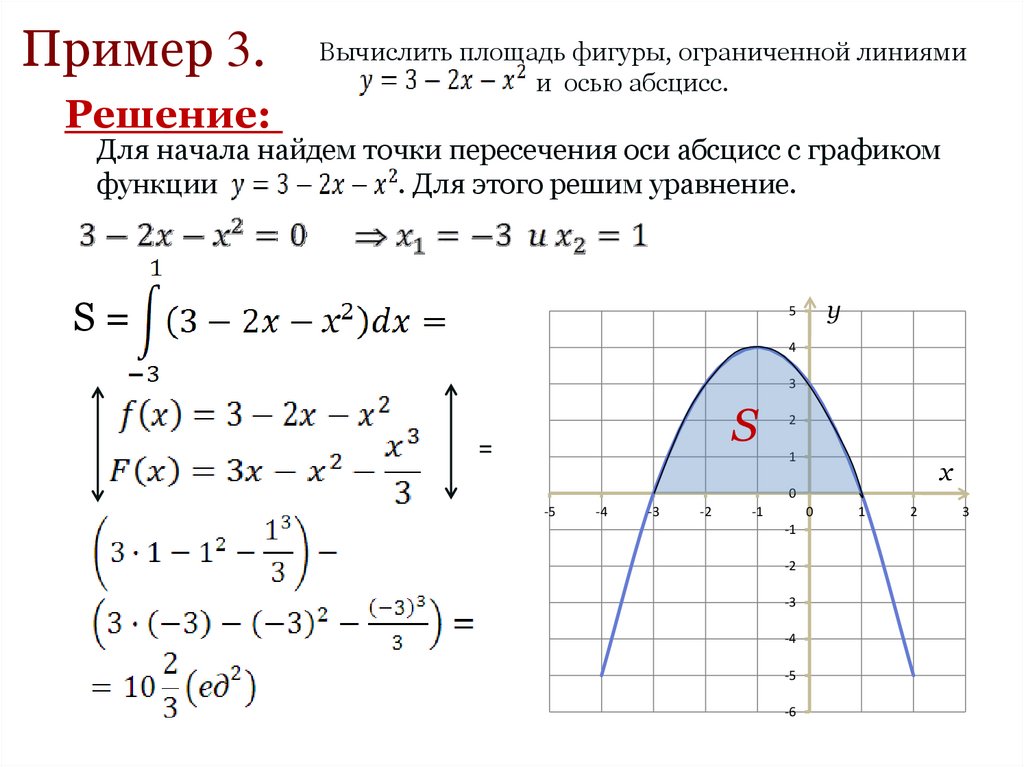
Пример 3.
Решение:
Вычислить площадь фигуры, ограниченной линиями
и осью абсцисс.
Для начала найдем точки пересечения оси абсцисс с графиком
функции
. Для этого решим уравнение.
S=
y
5
4
3
S
=
2
1
x
0
-5
-4
-3
-2
-1
0
-1
-2
-3
-4
-5
-6
1
2
3

3.

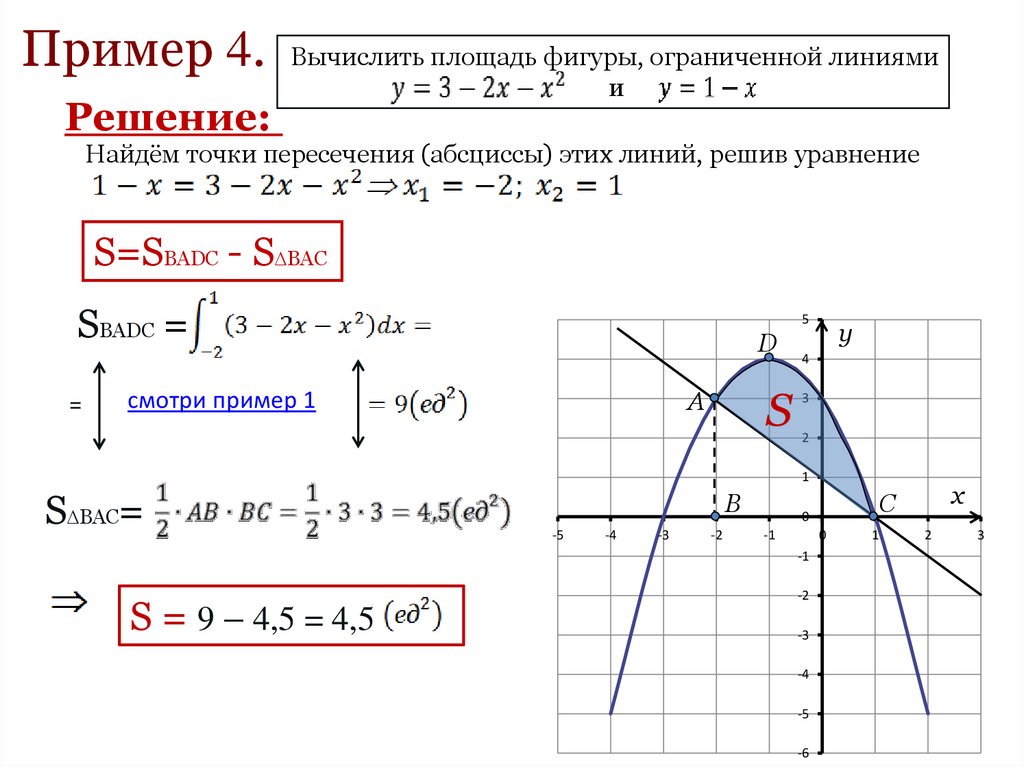
Пример 4.
Решение:
Вычислить площадь фигуры, ограниченной линиями
и
Найдём точки пересечения (абсциссы) этих линий, решив уравнение
S=SBADC - S BAC
SBADC =
=
5
D
S
A
смотри пример 1
y
4
3
2
1
S BAC=
B
-5
-4
-3
-2
-1
0
-1
S = 9 – 4,5 = 4,5
-2
-3
-4
-5
-6
x
C
0
1
2
3

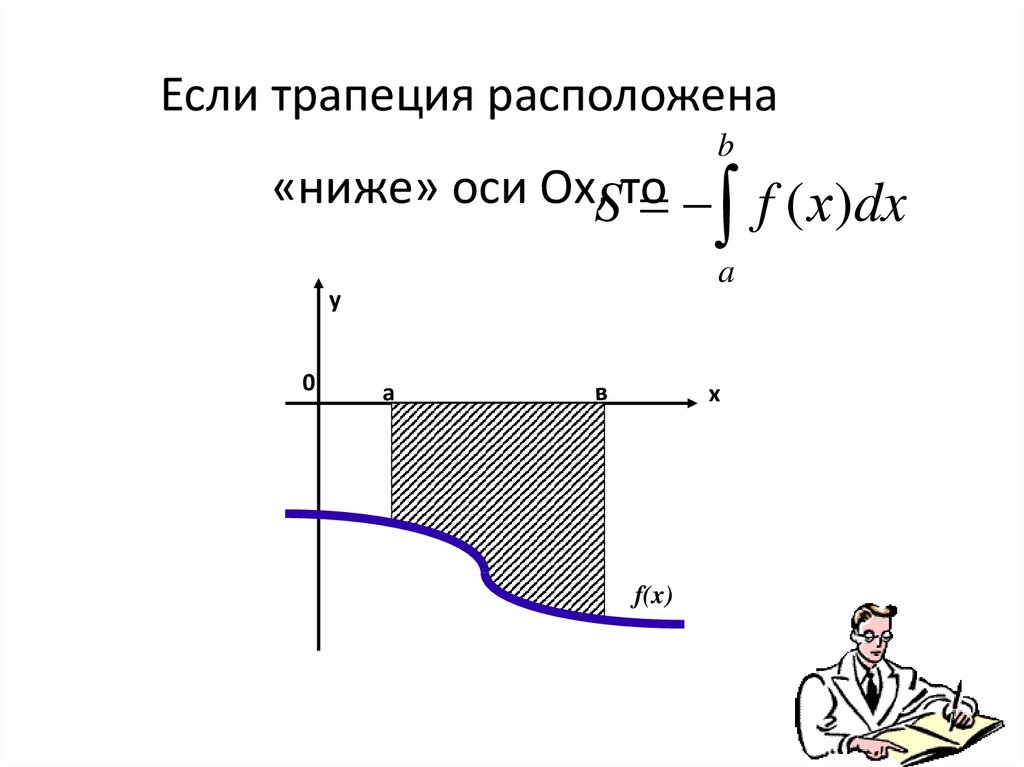
4. Если трапеция расположена «ниже» оси Ох, то

Если трапеция расположена
b
«ниже» оси Ох,Sто
f ( х)dx
a
y
а
х
f(x)
0

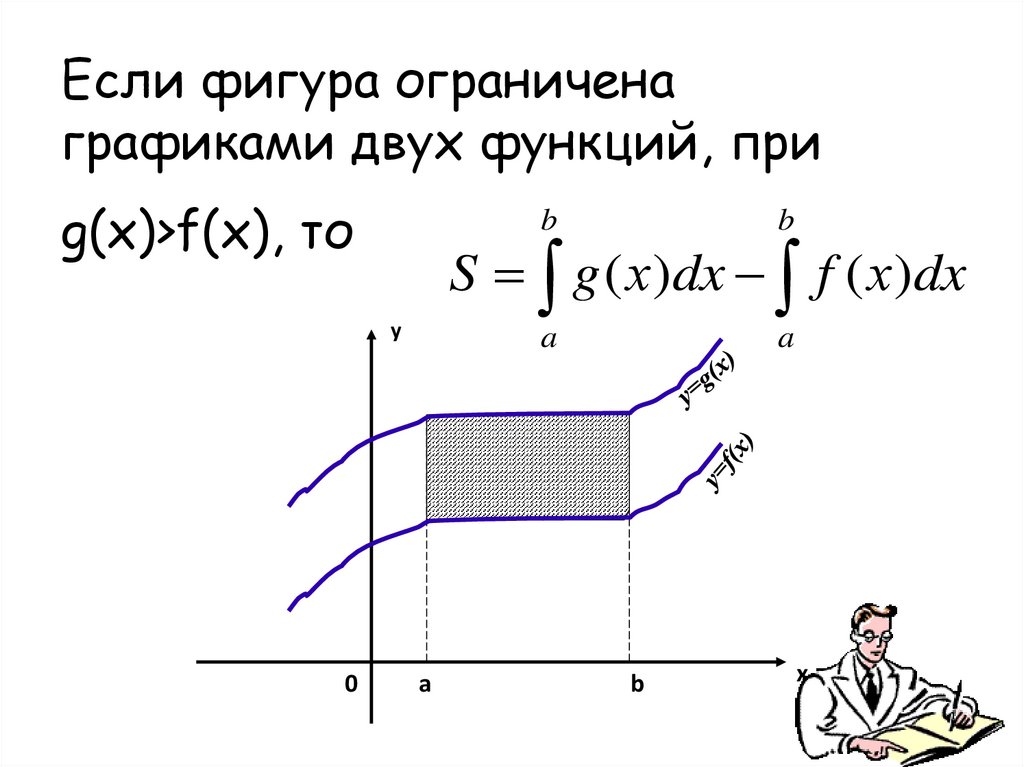
5.

Если фигура ограничена
графиками двух функций, при
g(х)>f(х), то
b
a
a
S g ( х)dx f ( х)dx
y
0
b
a
b
х

6. Закрепление

• П.21
• № 43 в
• № 45 в
• №47 в

7. Домашнее задание

• П.21
• № 43 а
• № 45 а
• № 47 а