Геометрический смысл определённого интеграла

1.

2.

?
План урока.
1. Понятие криволинейной трапеции.
2. Геометрический смысл определённого
интеграла.
3. Способы вычисления площадей
криволинейных трапеций с помощью
определённого интеграла.

3.

Задача:
Вычислить площадь земельного
участка, если он ограничен линиями
у=2х, у=0, х=1, х=2.

4. Как вычислить площадь данной фигуры?

s
У=2х
Х=1
У=0
Х=2

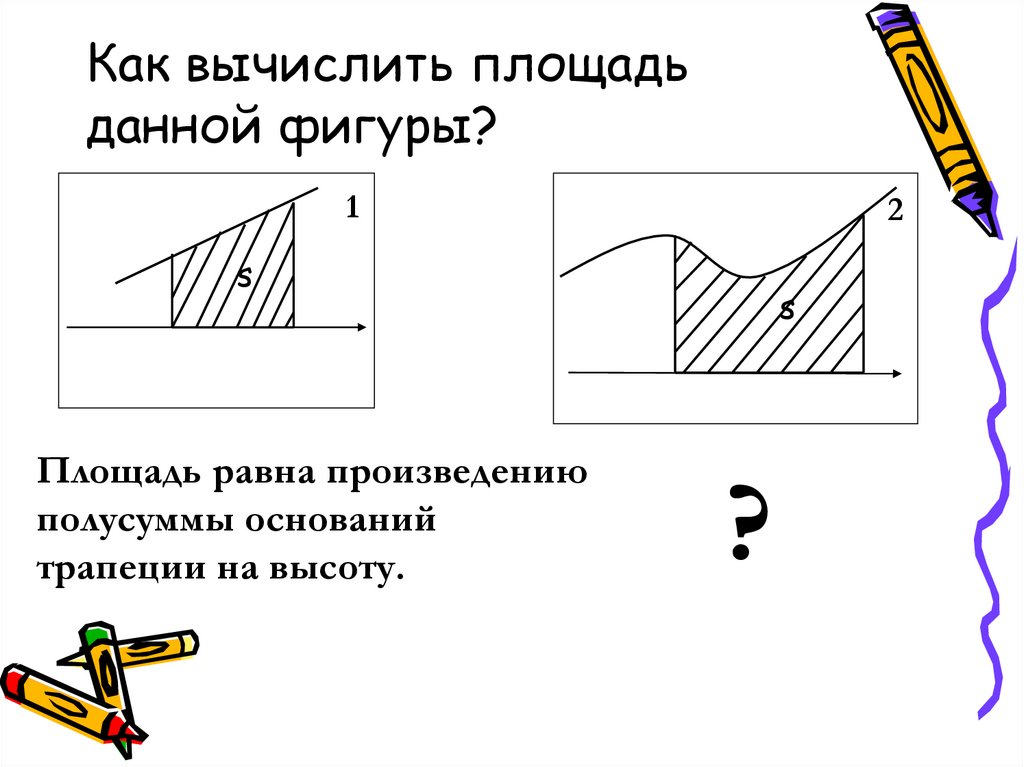
5. Как вычислить площадь данной фигуры?

1
2
s
Площадь равна произведению
полусуммы оснований
трапеции на высоту.
s
?

6. Рассмотрим следующие чертежи

y
y
а
0
0
а
x
b
y
0
а
b x
b
x

7. Определение: фигура, ограниченная графиком непрерывной и не меняющей своего знака на отрезке [a; b] функции, прямыми x=a, x=b и

отрезком [a; b]
называется криволинейной трапецией.
y
0
а
b
x

8. Как вычислить площадь данной фигуры?

1
2
s
Площадь равна произведению
полусуммы оснований
трапеции на высоту.
s
?

9. Геометрический смысл определённого интеграла.

f(x)>=0 на [a,b]
b
S
a
f ( x ) dx

10. Геометрический смысл определённого интеграла.

Плошадь фигуры, ограниченной
графиком непрерывной и не
меняющей своего знака на отрезке
[a; b] функции, прямыми x=a, x=b и
отрезком [a; b]
вычисляется по
формуле:
b
S
a
f ( x ) dx

11.

Задача:
Вычислить площадь земельного
участка, если он ограничен линиями
у=2х, у=0, х=1, х=2.

12.

Алгоритм нахождения площади
криволинейной трапеции:
1. Изобразить чертеж и убедится, является ли
данная фигура криволинейной трапецией
2. Вычислить площадь криволинейной трапеции
согласно геометрическому смыслу
определённого интеграла.

13. Задача: вычислить площадь эемельного участка, ограниченного линиями у=2х, у=0, х=1, х=2.

У=2х
Y
Решение:
S
0
Х=2
Х=1
1 2
2
x2 2
22
S 2xdx 2
x 22 12 4 1 3 кв. ед.
1
2 1
1
Ответ : S 3 кв. ед.
X

14. Задание.

Вычислить площадь фигуры, ограниченной линиями
y x 2 , y 0, x 1, x 3

15. Решение:

Y
у х2
0
1
3
X
x 3 3 33
13
27 1 26
2
S x dx
I
8 кв. ед.
3 1
3
3
3
3
3
1
3
2
Ответ: S=
8
2
кв. ед.
3

16. Возможные случаи расположения криволинейных трапеций.

Каким образом может
располагаться
график функции
y=f(x) относительно
оси ОХ?

17. Задание.

Вычислить площадь фигуры,
ограниченной линиями
y x 2 , y 0, x 1, x 3

18.

Решение:
Y
0
1
1
3
S
X
X=3
у х2
3
3
3
3
x
3
1
S x 2 dx
I
1
3
3 3
1
26
2
8
кв. ед.
3
3
3
27 1
3
3

19.

Решение:
Y
0
1
1
3
S
X
X=3
у х2
3
3
3
3
x
3
S х 2 dx
3 1
3
1
13
27 1
26 26
2
8 кв. е
3 3
3
3
3
3
Ответ: S= 8
2
кв. ед.
3

20. Если f(x)<0 на [а,b]

Если f(x)<0 на [а,b]
b
S
f ( x)dx
a

21. Задание.

Вычислить площадь фигуры,
ограниченной линиями
y x 3 , y 0, x 1, x 3

22. Решение

Y
График функции У х 3
пересекает ось ОХ.
-1
0
X=-1 S1
1
Найдём точки пересечения
графика функции с осью ОХ:
х3 0
х 0
У х3
S2 X=3
3
X

23. Решение

Y
-1
0
X=-1 S1
1
S2 X=3
3
У х3
4
4
4
0
x
0
1
1 1
3
S1 x dx
кв. ед.
4 1
4
4
4 4
1
0
3
4
4
4
3
x
3
0
81
1
3
S2 x dx
20 кв. ед.
40 4 4
4
4
0
1
1 1 25 26
1
S 20 6 кв. ед.
4
4 4 4
4
2
X

24. График функции y=f(x) пересекает ось ОХ в точке с [a,b]

S=S1+S2
S
с
b
а
c
f(x)dx f ( x)dx

25. Если две функции y=f(x) и y= Ф (x) непрерывны на отрезке [a,b] и их графики не имеют общих точек на [a,b]

26. Если две функции y=f(x) и y= Ф (x) непрерывны на отрезке [a,b] и их графики не имеют общих точек на [a,b]

S2
b
SS 1
f ( x)dx
b
a
b
f ( x)dx
S2
a
Ф( x)dx
a
b
S
f
(
x
)
(
x
)
dx
a

27. Задание.

Вычислить площадь фигуры, ограниченной линиями
y x 2 3, y 2 х 8, x 1, x 3

28. Решение:

Y
у х2 3
3
S (2 x 8 ( x 2 3)) dx
S
1
-1
У=2х+8
0
1
3
X

29. Решение:

3
3
3
3
x 2 x3
S (2 x 8 ( x 3)) dx (2 х 8 х 3)dx (2 x x 5)dx (2 5 x)
1
2 3
1
1
1
2
2
2
32 33
( 1) 2 ( 1)3
9 27
1 1
2 5 3 (2
5 ( 1)) 2 15 (2 15)
2 3
2
3
2 3
2 3
1 9 42 1 32
2
3 14
10 кв. ед.
3
3
3
3
2
Ответ : S 10 кв. ед.
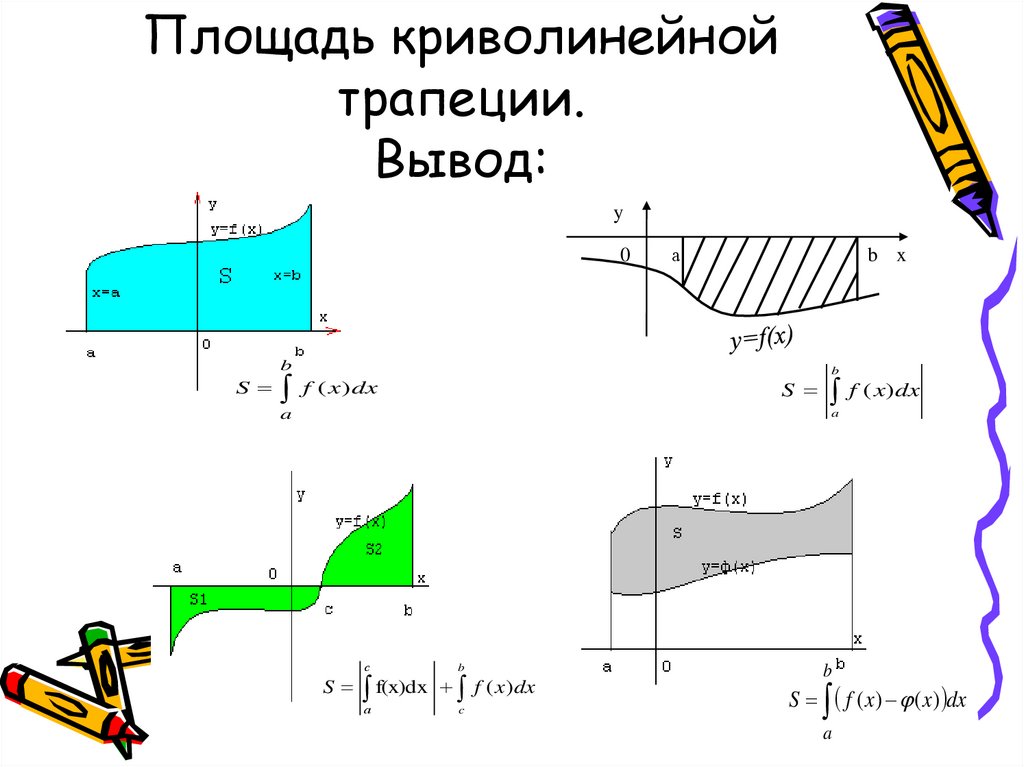
3

30. Площадь криволинейной трапеции. Вывод:

y
0
а
b x
b
S
b
S
f ( x ) dx
a
f ( x)dx
a
S
с
b
а
c
f(x)dx f ( x)dx
b
S
f ( x) ( x) dx
a

31. Графики функции у=f(x) имеет множество точек пересечения с осью (ОХ)

Графики функции у=f(x) имеет
множество точек пересечения
с осью (ОХ)
S3
S1
S2
S4
S S1 S 2 S3 S 4
c
S f(x)dx
a
d
e
b
c
d
e
f ( x)dx f ( x)dx f ( x)dx

32.

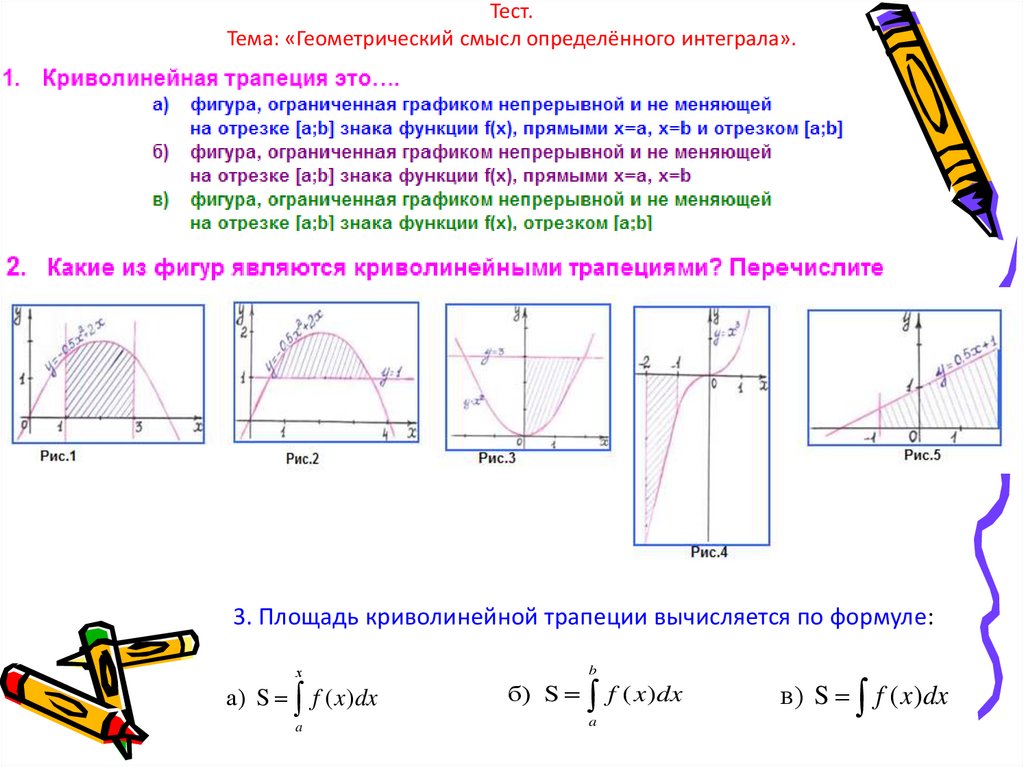
Тест.
Тема: «Геометрический смысл определённого интеграла».
3. Площадь криволинейной трапеции вычисляется по формуле:
х
а) S f ( x)dx
a
b
б) S
f ( x)dx
a
в) S f ( x)dx

33.

Ну, кто говорил, что всё сложно и
постичь это всё невозможно?
Всё оказалось доступным, полезным,
а также достаточно интересным