Средняя линия треугольника

1.

2.

Средней линией треугольника называется
отрезок, соединяющий середины двух его
С
сторон.
А
В
Сколько средних линий можно построить в
треугольнике?

3.

Теорема. Средняя линия треугольника параллельна
одной из его сторон и равна половине этой стороны.
Дано: ABC, МN – средняя линия
1
Доказать: МN II АС, MN = 2 АС
B Доказательство: В общий,
BN
1
BM
=
=
BC
2
BA
М
MBN
N
ABC
по 2 признаку
MN
1
1 АС
MN
=
=
;
2
AC
2
1= 2 CУ, значит, МN II АС.
А
C

4.

УСТНО:
Какую сторону треугольника АВС можно найти?
С
N
F
7 см
14
В
А
O

5.

УСТНО:
Найдите стороны треугольника АВС.
С
F
16
8 см
7 см
14
5,5см
11
А
N
В
O

6.

УСТНО:
Найдите периметр ∆АВС, если
периметр ∆ОFN равен 23 см.
С
N
F
Р=23см
В
А
O

7.

УСТНО:
Найдите х, у, РАВС.
В
x10
6
М
N
8
РАВС = 48
А
y
16
С

8.

9.

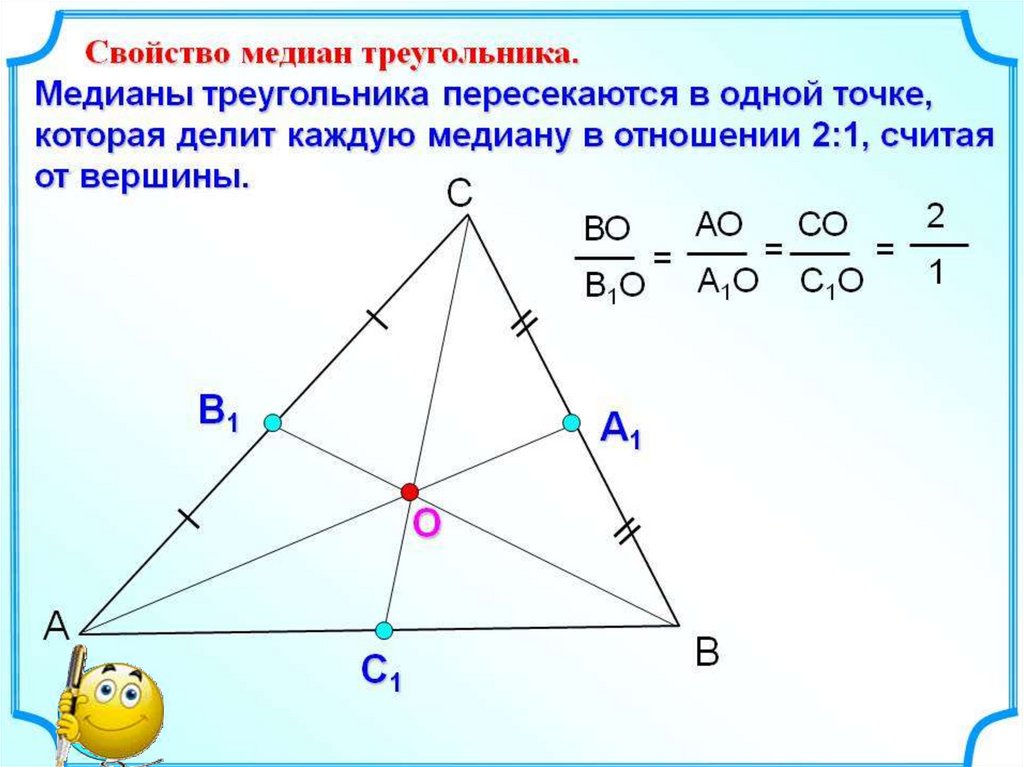
УСТНО:
ВО
ОВ1
ВВ1 = 15 см
2
=
15 : 3 = 5 см (1 часть)
1
В1
Найти ВО и ОВ1
С
5
А1
О
10
А
С1
В

10.

УСТНО:
ВО
ОВ1
ОВ1 = 4 см
Найти ВО и ВВ1
2
=
ОВ1 = 4 см (1 часть)
1
В1
С
4
А1
О
8
А
С1
В

11.

УСТНО:
СО
ОС1
ОС = 7 см
2
=
Найти СО и СС1
7 : 2 = 3,5 см (1 часть)
1
С
7
В1
О
А1
3,5
А
С1
В

12.

№ 1. Средняя линия треугольника на 3,6 см
меньше основания треугольника. Найдите сумму
средней линии треугольника и основания.
№ 2. АВСD – параллелограмм, АС и ВD –
диагонали параллелограмма, т.О – точка их
пересечения, ОЕ = 4 см и ОF = 5 см – средние
линии треугольника АВС. Найти периметр
параллелограмма.

13.

№ 4. Периметр параллелограмма АВСD равен
60 см, а длина его диагонали ВD равна 18 см.
Точки К и Р – середины сторон АD и АВ
соответственно. Найдите периметр
пятиугольника ВСDКР.

14.

ТЕОРИЯ: выучить теорию
на стр. 145 – 146;
ЗАДАЧИ: решить № 566, 567, 568