Работа с текстом на уроках математики

1.

Работа с текстом на уроках
математики
Чмарина Ирина Александровна,
учитель математики МБОУ БСОШ №3

2.

Ключевые направления формирования умений
работы с текстом
выделение главного в тексте;
составление примеров, аналогичных приведенным в тексте;
умение найти в тексте ответ на поставленный вопрос;
грамотно пересказать прочитанный текст;
умение составить план прочитанного;
воспроизводить текст по предложенному плану;
умение пользоваться образцами решения задач;
запоминание определений, формул, теорем;
работа с иллюстрациями (рисунками, чертежами,
диаграммами);
• использование новой теории в различных учебных и
жизненных ситуациях;
• подтверждение научных фактов;
• конспектирование новой темы.

3.

«Тонкие» и « толстые» вопросы
Составить вопросы по теме, по тексту параграфа и т.д.
«Тонкие» вопросы – вопросы, требующие простого,
односложного ответа.
Кто..? Что…? Когда…? Может…? Мог ли…? Было ли…? Будет…?
Согласны ли вы…? Верно ли…?
«Толстые» вопросы – вопросы, требующие подробного,
развёрнутого ответа.
Объясните почему….? Почему вы думаете….?
Предположите, что будет если…? В чём различие…?
Почему вы считаете….?

4.

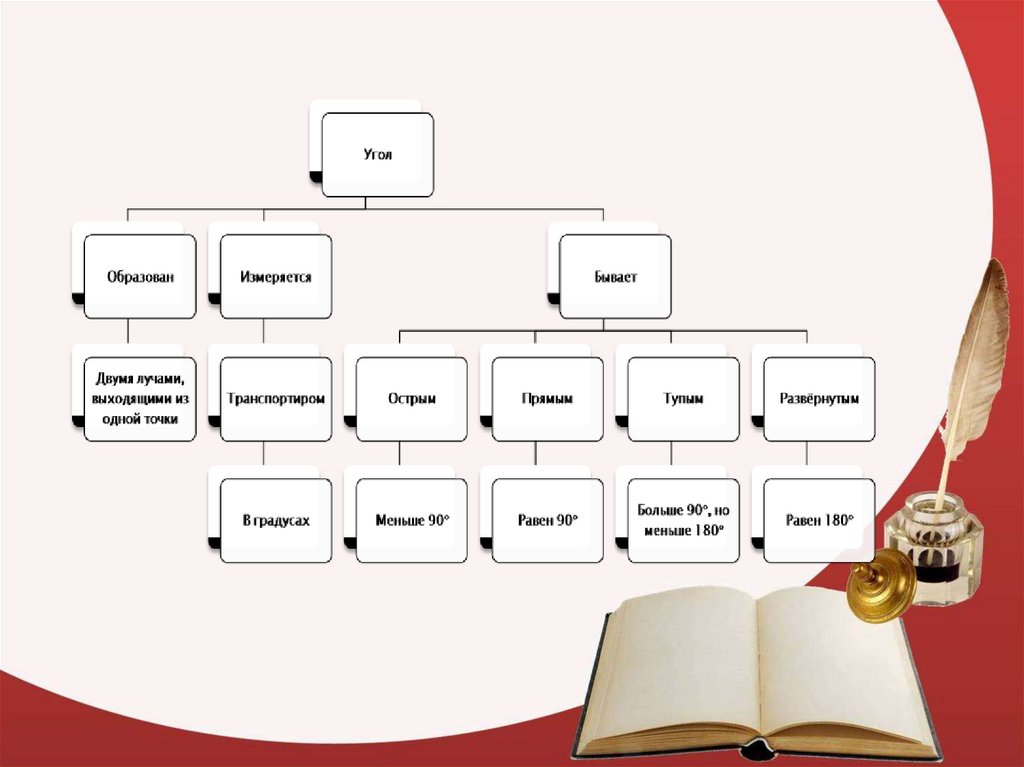
«Кластер»
Кластер – способ графической организации
учебного материала.
На листке (доске) записывается или
зарисовывается основное слово (идея, тема), а по
сторонам от него фиксируются идеи (слова,
рисунки), с ним связанные.

5.

6.

«Верно или неверно утверждение»
1) Треугольник является объемной фигурой.
2) Треугольником называется геометрическая фигура,
состоящая из трех точек, не лежащих на одной прямой
и соединенных попарно прямыми.
3) Если в треугольнике две стороны равны, то
треугольник называется равнобедренным.
4) Внешним углом треугольника называется угол,
смежный с каким-нибудь углом этого треугольника.
5) В треугольнике углы при основании равны.

7.

«Незаконченное предложение»
1. Натуральное число называют простым, если оно __________.
2. Если числитель и ____________ дроби умножить на _______
и ________ натуральное число, то получится __________ ей
дробь.

8.

«Оценка текста»
Предлагается не читать текст абзац за
абзацем, а оценить содержание изучаемого
параграфа.
Какие слова выделены курсивом или жирным
шрифтом? Как по-вашему, почему они
выделены? Какое имя (слово, термин) чаще
всего встречается в данном параграфе?

9.

«Составление различных формулировок для
одного и того же утверждения или
определения.»
Предлагается придумать как можно больше
различных формулировок одного и того же
утверждения, записать на листок. Далее проводится
обсуждение предложенных утверждений или всем
классом, или возможна работа в парах и группах.

10.

Первый признак равенства треугольников. Если две
стороны и угол между ними одного треугольника равны
соответственно двум сторонам и углу между ними другого
треугольника, то такие треугольники равны.
1.Если в двух треугольниках соответственно равны
две стороны и угол между ними, то эти треугольники равны.
2. При соответственно равных двух сторонах и угла
между ними в двух треугольниках, эти треугольники являются равными.
3.Равность двух треугольников может доказываться
соответственной равностью двух сторон и угла
между ними.

11.

«Угадай-ка!»
Вопрос - задание: Найдите в череде слов одно из
самых важных математических предложений,
которое вы встретили в тексте.
Всеотпонперестановкидорогаслагаемыхдобрянка
суммапонелазнаменяется
«Составление краткой записи задачи»

12.

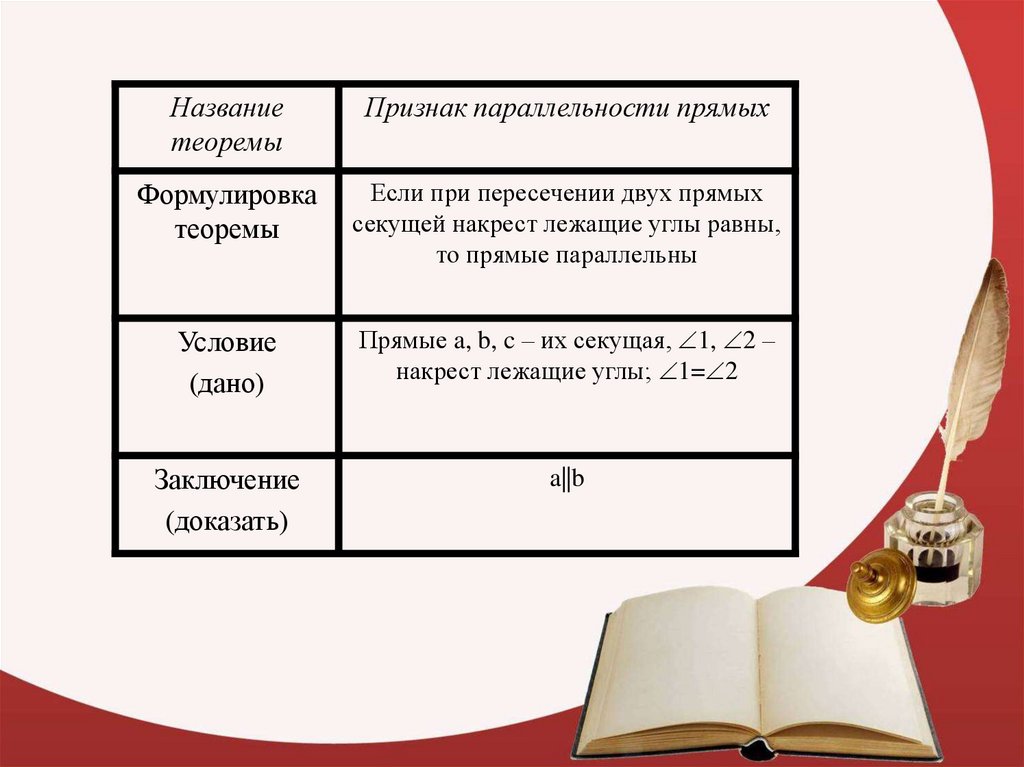
Название
теоремы
Признак параллельности прямых
Формулировка
теоремы
Если при пересечении двух прямых
секущей накрест лежащие углы равны,
то прямые параллельны
Условие
(дано)
Прямые a, b, c – их секущая, 1, 2 –
накрест лежащие углы; 1= 2
Заключение
(доказать)
a||b

13.

Название
теоремы
Признак параллельности
прямых
Свойства параллельных
прямых
Формулировка
теоремы
Если при пересечении двух
прямых секущей накрест
лежащие углы равны, то
прямые параллельны
Если две параллельные
прямые пересечены
секущей, то накрест лежащие
углы равны.
Условие
(дано)
Прямые a, b, c – их секущая,
1, 2 – накрест лежащие
углы; 1= 2
Прямые a, b, c – их секущая,
1, 2 – накрест лежащие
углы; a||b
Заключение
(доказать)
a||b
1= 2