Похожие презентации:
Санкт-Петербург. Приморский район
1.
Государственное бюджетное общеобразовательное учреждениеСредняя общеобразовательная школа №58
Санкт-Петербург
Приморский район
2.
Цели урока :Установить связь между фигурами, изучаемыми в
данной теме;
Систематизировать
свойства
и
признаки
четырехугольников, изученных на уроках геометрии;
Закрепить в процессе решения задач полученные
знания и навыки;
Создать у школьников положительную мотивацию к
выполнению умственных и практических заданий;
Совершенствовать коммуникативные умения учащихся в
совместной
деятельности
и
информационно
–
познавательную компетентность учащихся.
3.
Четырёхугольником называется фигура, котораясостоит из четырёх точек (вершин) и четырёх отрезков (сторон),
которые последовательно соединяют вершины. При этом
никакие три из данных точек не должны лежать на одной прямой,
а соединяющие их отрезки не должны пересекаться.
Четырёхугольник называется выпуклым, если он лежит по
одну сторону от каждой прямой, проходящей через две
его соседние вершины.
В
С
выпуклый
невыпуклый
D
А
Стороны,
исходящие
из
одной
вершины,
смежными.
Вершины, являющиеся концами одной стороны,
соседними.
Стороны,
не
имеющие
общих
вершин,
противолежащими.
Отрезки, соединяющие противолежащие вершины,
диагоналями.
называются
называются
называются
называются
4.
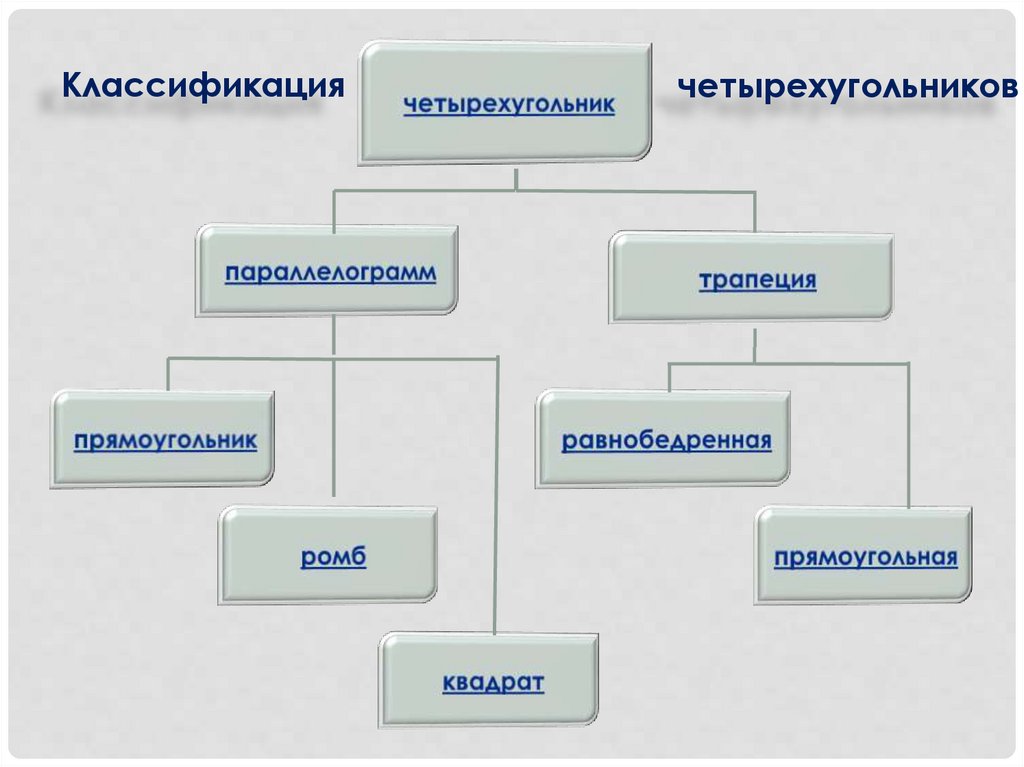
Классификациячетырехугольников
5.
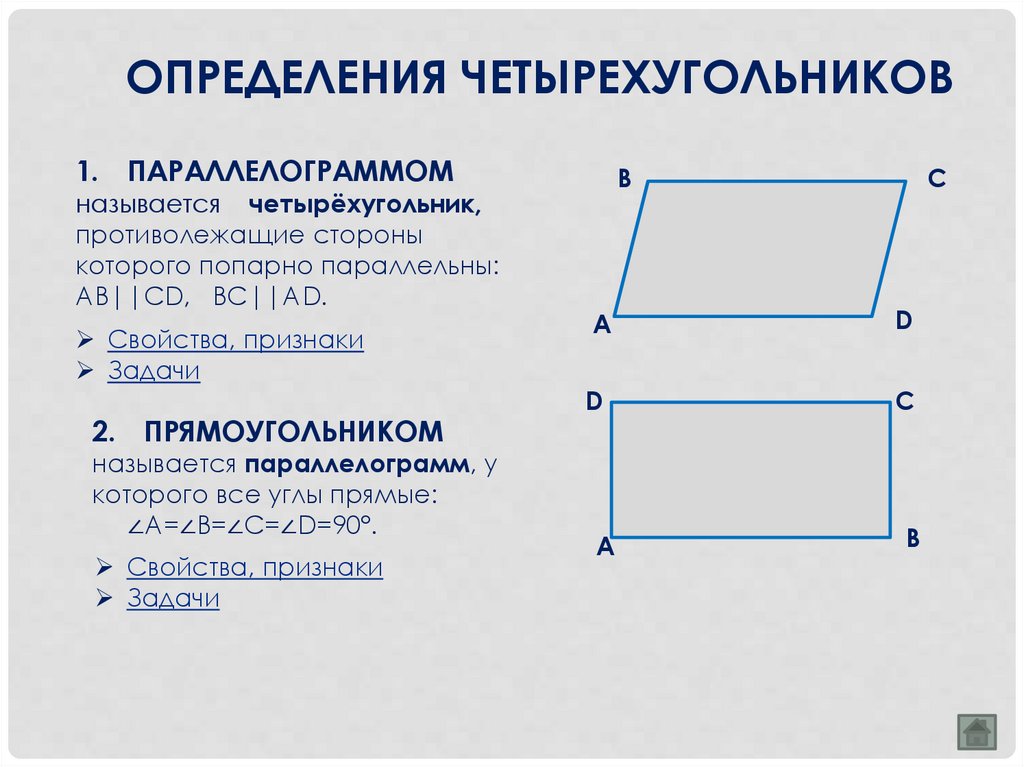
ОПРЕДЕЛЕНИЯ ЧЕТЫРЕХУГОЛЬНИКОВ1. ПАРАЛЛЕЛОГРАММОМ
называется четырёхугольник,
противолежащие стороны
которого попарно параллельны:
AB||CD, BC||AD.
Свойства, признаки
Задачи
2. ПРЯМОУГОЛЬНИКОМ
называется параллелограмм, у
которого все углы прямые:
∠A=∠B=∠C=∠D=90°.
Свойства, признаки
Задачи
В
А
D
А
С
D
С
В
6.
ОПРЕДЕЛЕНИЯ ЧЕТЫРЕХУГОЛЬНИКОВА
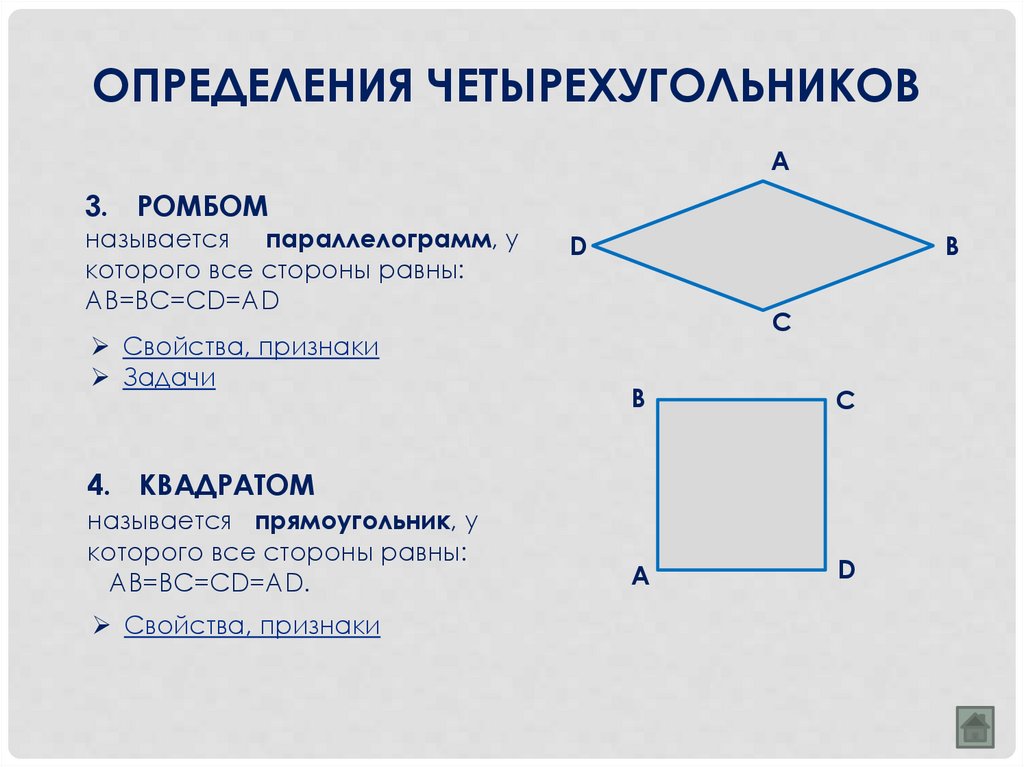
3. РОМБОМ
называется параллелограмм, у
которого все стороны равны:
AB=BC=CD=AD
Свойства, признаки
Задачи
D
В
С
В
С
А
D
4. КВАДРАТОМ
называется прямоугольник, у
которого все стороны равны:
AB=BC=CD=AD.
Свойства, признаки
7.
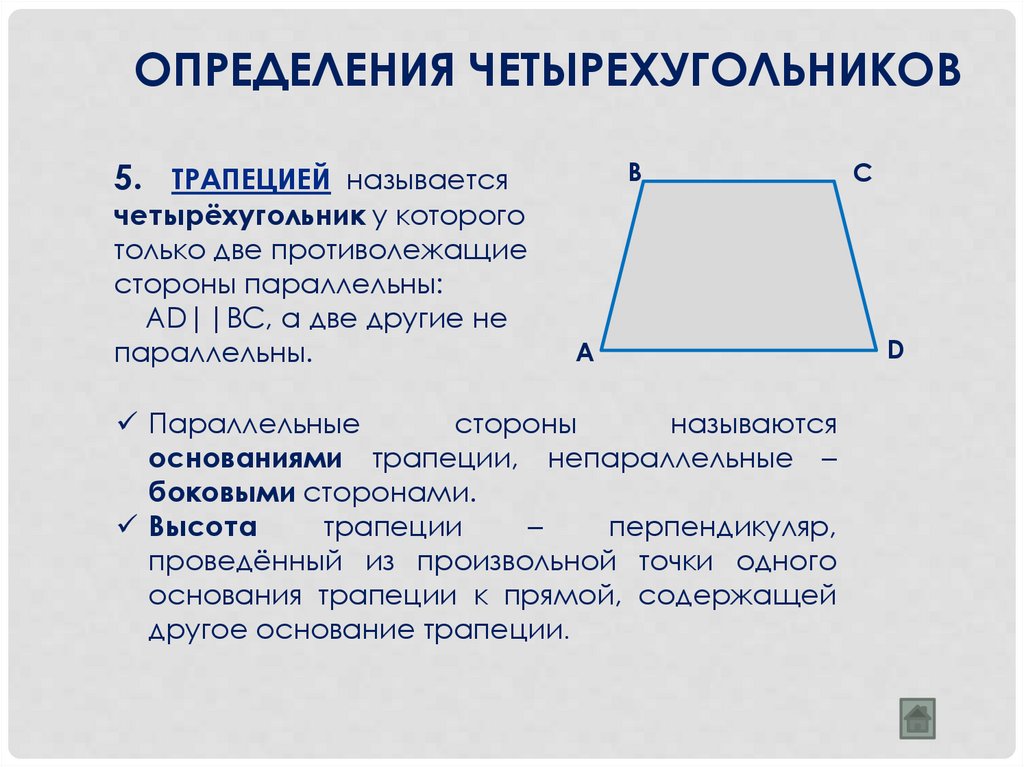
ОПРЕДЕЛЕНИЯ ЧЕТЫРЕХУГОЛЬНИКОВ5. ТРАПЕЦИЕЙ называется
четырёхугольник у которого
только две противолежащие
стороны параллельны:
AD||BC, а две другие не
параллельны.
В
А
Параллельные
стороны
называются
основаниями трапеции, непараллельные –
боковыми сторонами.
Высота
трапеции
–
перпендикуляр,
проведённый из произвольной точки одного
основания трапеции к прямой, содержащей
другое основание трапеции.
С
D
8.
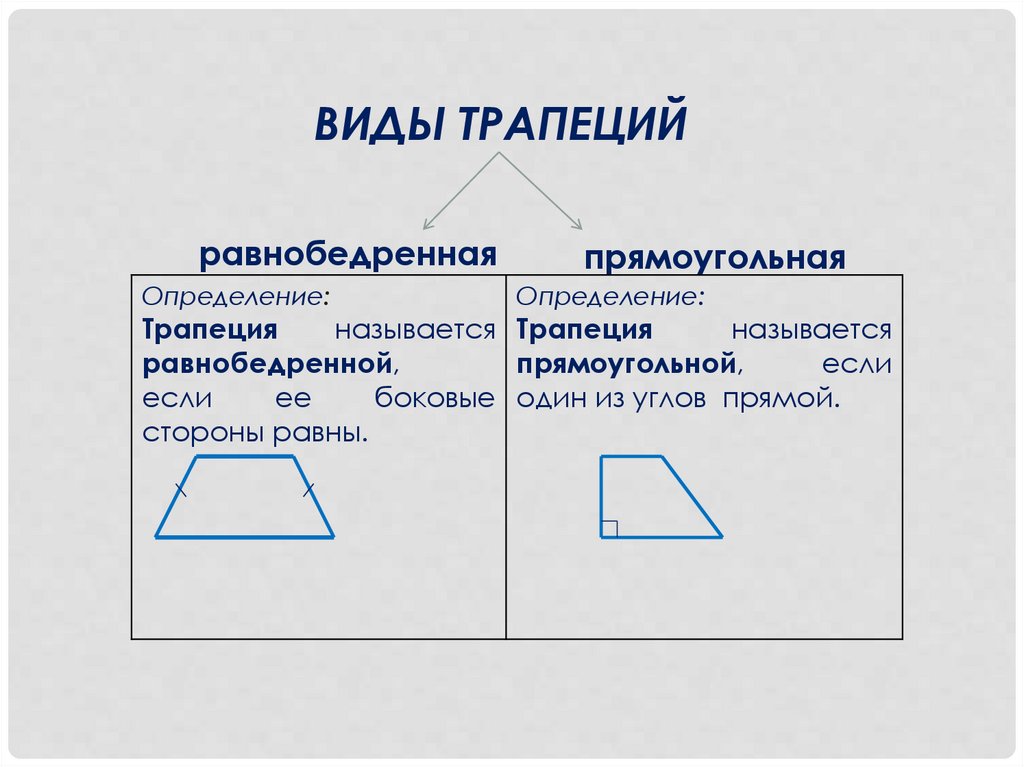
ВИДЫ ТРАПЕЦИЙравнобедренная
Определение:
прямоугольная
Определение:
Трапеция
называется Трапеция
называется
равнобедренной,
прямоугольной,
если
если
ее
боковые один из углов прямой.
стороны равны.
9.
ПАРАЛЛЕЛОГРАММСвойства
В параллелограмме АВСД:
Противоположные стороны
равны;
Противоположные углы равны;
Диагонали точкой пересечения
делятся пополам;
Дополнительные свойства:
⦟А+⦟В=⦟С+⦟D=⦟В+⦟С=
=⦟А+⦟D=180˚;
Биссектриса угла отсекает от
него равнобедренный
треугольник;
Е
В
С
О
А
D
Диагональ параллелограмма
делит его на два равных
треугольника.
Признаки
(признаки фигуры отвечают на
вопрос «как узнать что фигура
является …?»)
АВСД параллелограмм, если:
У четырехугольника две стороны
равны
и параллельны;
У четырехугольника
противоположные стороны
попарно равны;
У четырёхугольника
противоположные углы равны;
У четырехугольника диагонали
точкой пересечения делятся
пополам.
10.
ПРЯМОУГОЛЬНИКСвойства
Обладает всеми свойствами
параллелограмма.
В прямоугольнике АВСД:
Свойство противолежащих сторон и
углов:
Противоположные стороны и углы
равны;
Свойство диагоналей:
Диагонали пересекаются и точкой
пересечения делятся пополам.
Отличительное свойство, только
прямоугольника:
В
Диагонали прямоугольника равны.
Дополнительные свойства:
Диагонали делят его на два равных
треугольника;
Сумма углов, прилегающих к одной А
стороне, равна 180 °.
Признаки
АВСД прямоугольник, если:
В параллелограмме все
углы равны;
В параллелограмме один
угол прямой;
В четырехугольнике три
угла прямые;
В параллелограмме
диагонали равны.
С
D
11.
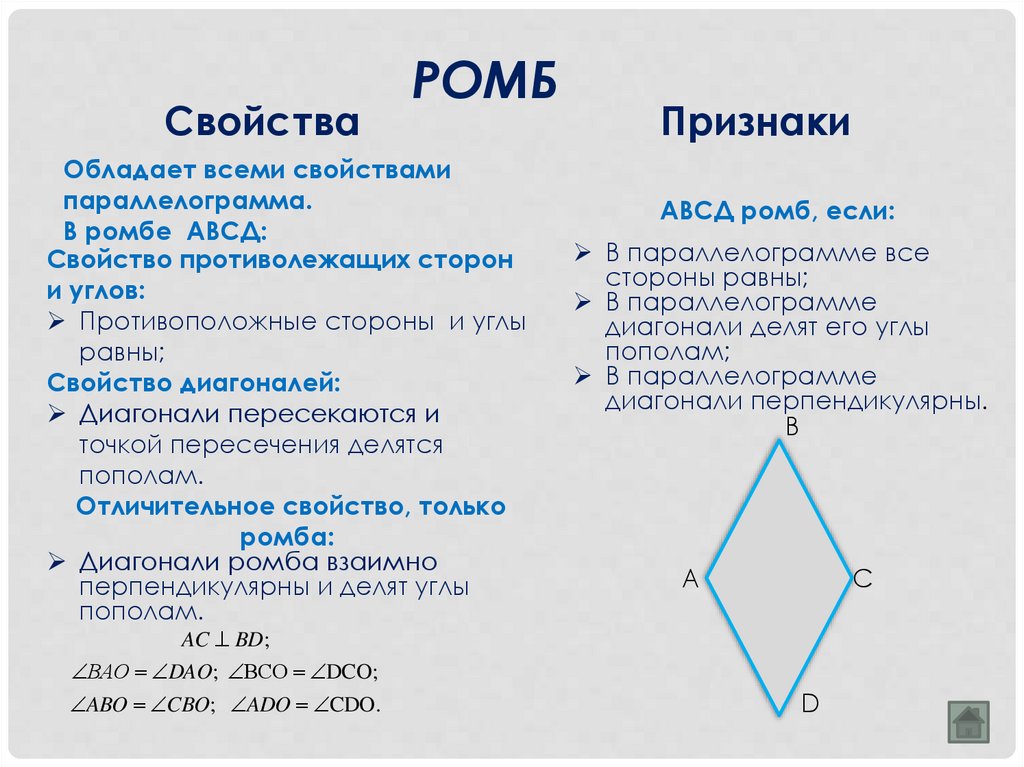
СвойстваРОМБ
Обладает всеми свойствами
параллелограмма.
В ромбе АВСД:
Свойство противолежащих сторон
и углов:
Противоположные стороны и углы
равны;
Свойство диагоналей:
Диагонали пересекаются и
точкой пересечения делятся
пополам.
Отличительное свойство, только
ромба:
Диагонали ромба взаимно
перпендикулярны и делят углы
пополам.
Признаки
АВСД ромб, если:
В параллелограмме все
стороны равны;
В параллелограмме
диагонали делят его углы
пополам;
В параллелограмме
диагонали перпендикулярны.
В
А
С
AC BD ;
ВАО DAO; ВCO DCO;
ABO CBO; ADO CDO.
D
12.
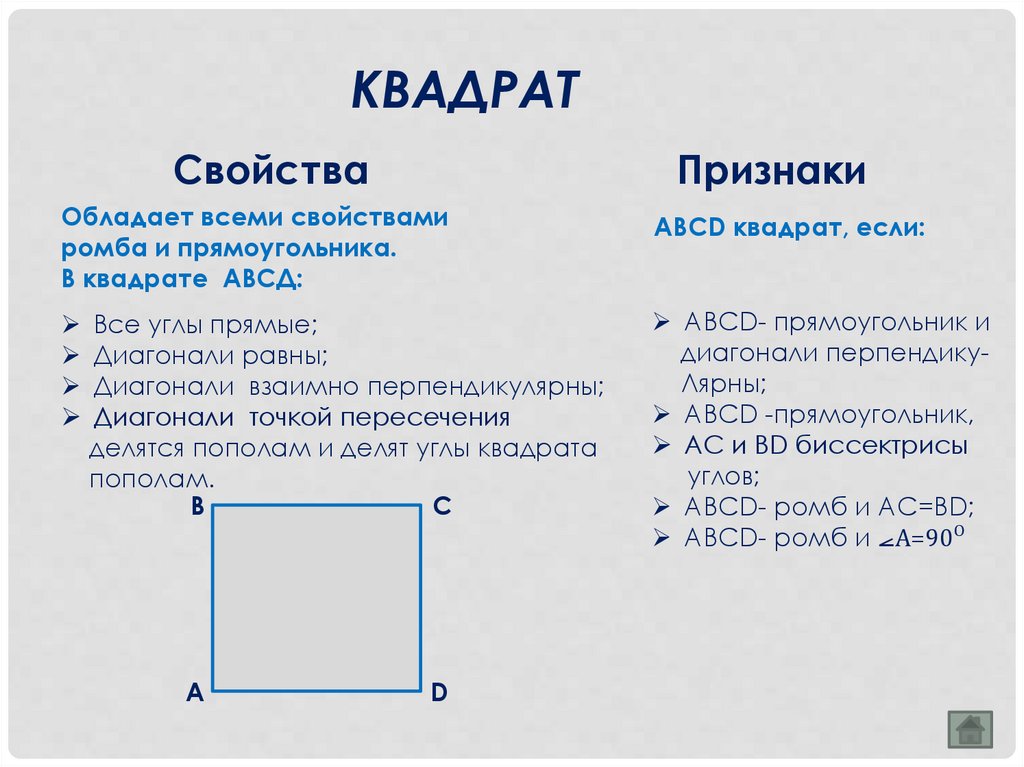
КВАДРАТСвойства
Признаки
Обладает всеми свойствами
ромба и прямоугольника.
В квадрате АВСД:
Все углы прямые;
Диагонали равны;
Диагонали взаимно перпендикулярны;
Диагонали точкой пересечения
делятся пополам и делят углы квадрата
пополам.
В
С
А
D
АВСD квадрат, если:
АВСD- прямоугольник и
диагонали перпендикуЛярны;
АВСD -прямоугольник,
АС и ВD биссектрисы
углов;
АВСD- ромб и АС=ВD;
АВСD- ромб и ⦟А=90ᴼ
13.
МАТЕМАТИЧЕСКИЙ ДИКТАНТ1.Диагонали пересекаются и точкой пересечения
делятся пополам у ...
2.Диагонали равны у ...
3.Углы, прилегающие к одной стороне, равны у …
4.Диагонали перпендикулярны у ...
5.Диагонали делят углы пополам у ...
6.Все углы равны у ...
7.Диагонали равны и перпендикулярны у ...
8.Какой параллелограмм обладает всеми
перечисленными свойствами? …
Ответы написать в тетради, самопроверка по образцу
14.
ОТВЕТЫ:1.
2.
3.
4.
5.
6.
7.
8.
Диагонали пересекаются и точкой пересечения
делятся пополам у прямоугольника, ромба,
квадрата.
Диагонали равны у прямоугольника, квадрата.
Углы, прилегающие к одной стороне, равны
у прямоугольника, квадрата.
Диагонали перпендикулярны у ромба, квадрата.
Диагонали делят углы пополам у ромба, квадрата.
Все углы равны у прямоугольника, квадрата.
Диагонали равны и перпендикулярны у квадрата.
Какой параллелограмм обладает всеми
перечисленными свойствами? (Квадрат)
15.
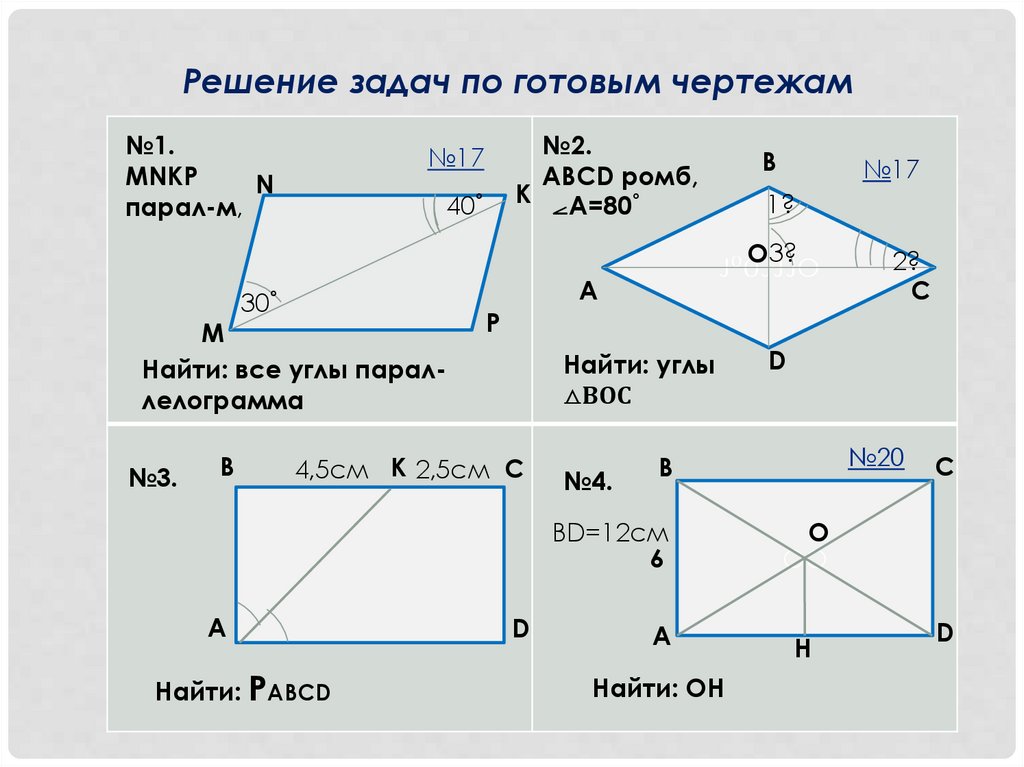
Решение задач по готовым чертежам№1.
MNKP
N
парал-м,
40˚
M
Найти: все углы параллелограмма
№3.
В
1?
Найти: углы
⧍ВОС
№4.
D
D
№20
В
ВD=12см
6
Найти: РАВСD
2?
С
P
4,5см К 2,5см С
А
№17
O3?
JᴼОJJJО
А
30˚
В
№2.
АВСD ромб,
K ⦟А=80˚
№17
А
Найти: ОН
С
O
ОО
H
D
16.
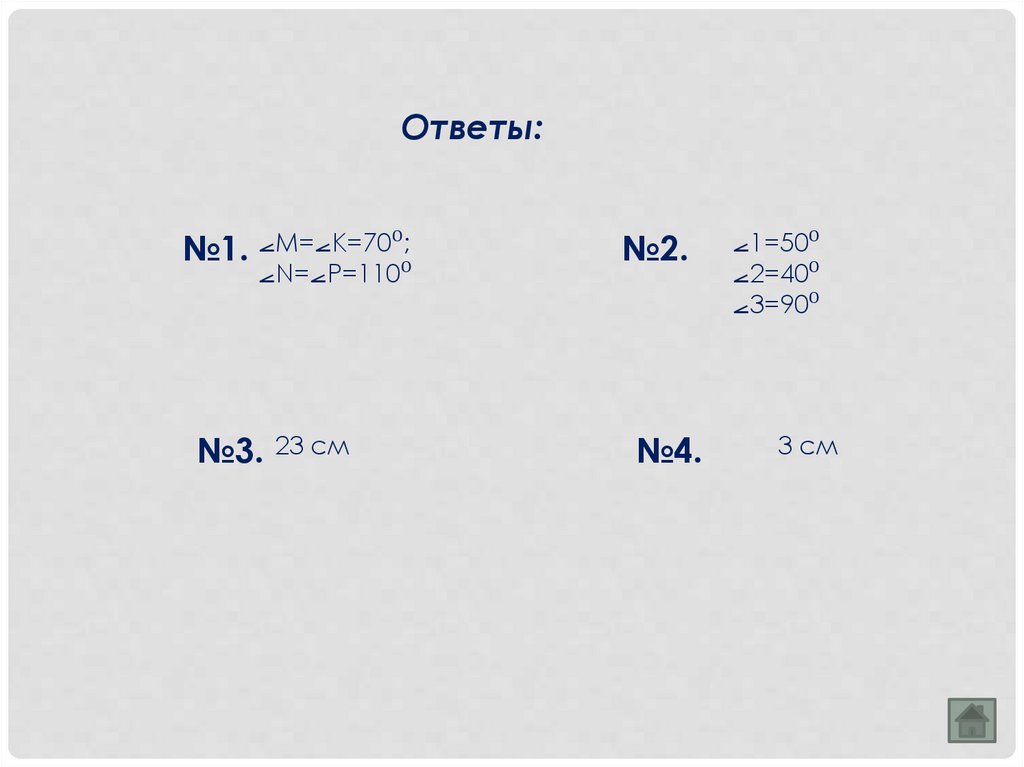
Ответы:№1. ⦟M=⦟K=70ᴼ;
⦟N=⦟P=110ᴼ
№3.
23 см
№2.
№4.
⦟1=50ᴼ
⦟2=40ᴼ
⦟3=90ᴼ
3 см
17.
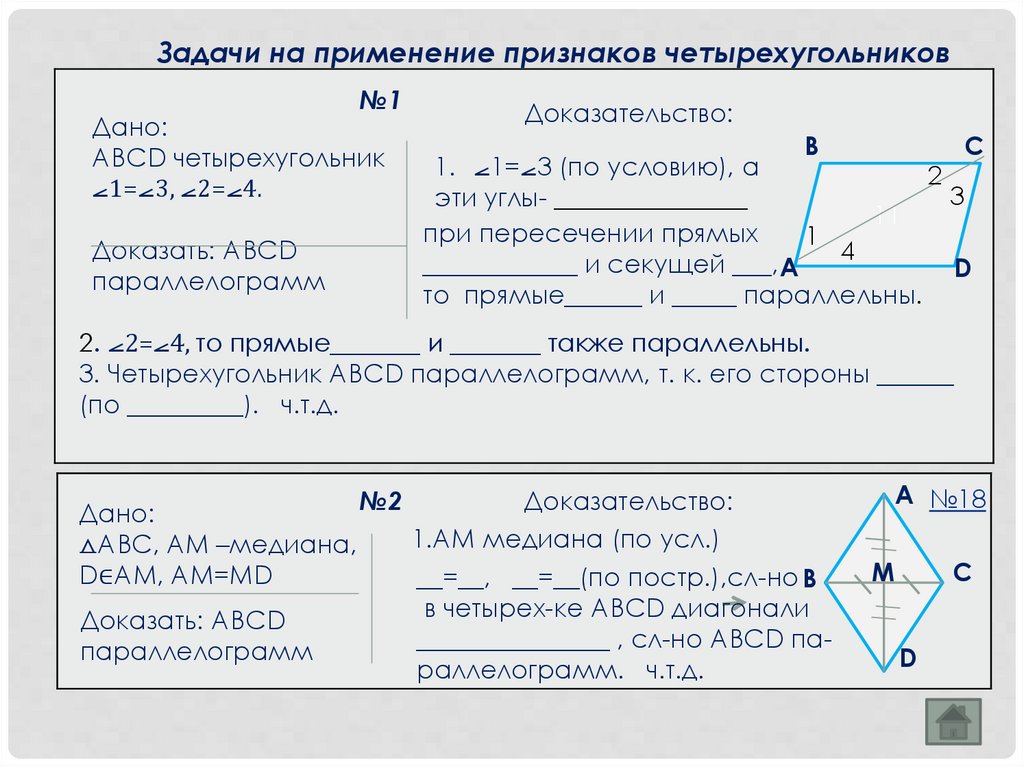
Задачи на применение признаков четырехугольников№1
Дано:
АВСD четырехугольник
⦟1=⦟3, ⦟2=⦟4.
Доказать: АВСD
параллелограмм
Доказательство:
В
С
1. ⦟1=⦟3 (по условию), а
2
3
эти углы- _______________
11
при пересечении прямых
1
4
____________ и секущей ___, А
D
то прямые______ и _____ параллельны.
2. ⦟2=⦟4, то прямые_______ и _______ также параллельны.
3. Четырехугольник АВСD параллелограмм, т. к. его стороны ______
(по _________). ч.т.д.
Доказательство:
№2
Дано:
1.АМ медиана (по усл.)
⧍АВС, АМ –медиана,
D∈АМ, АМ=МD
__=__, __=__(по постр.),сл-но В
в четырех-ке АВСD диагонали
Доказать: АВСD
_______________ , сл-но АВСD папараллелограмм
раллелограмм. ч.т.д.
А №18
С
М
D
18.
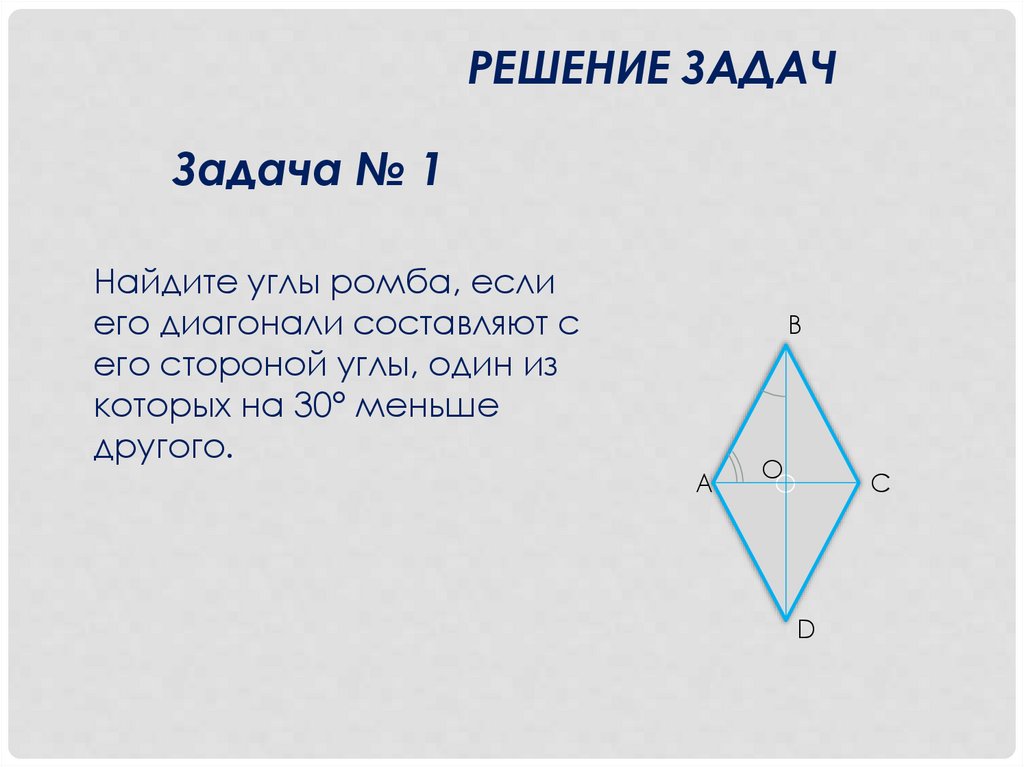
РЕШЕНИЕ ЗАДАЧЗадача № 1
Найдите углы ромба, если
его диагонали составляют с
его стороной углы, один из
которых на 30° меньше
другого.
В
А
О
О
D
С
19.
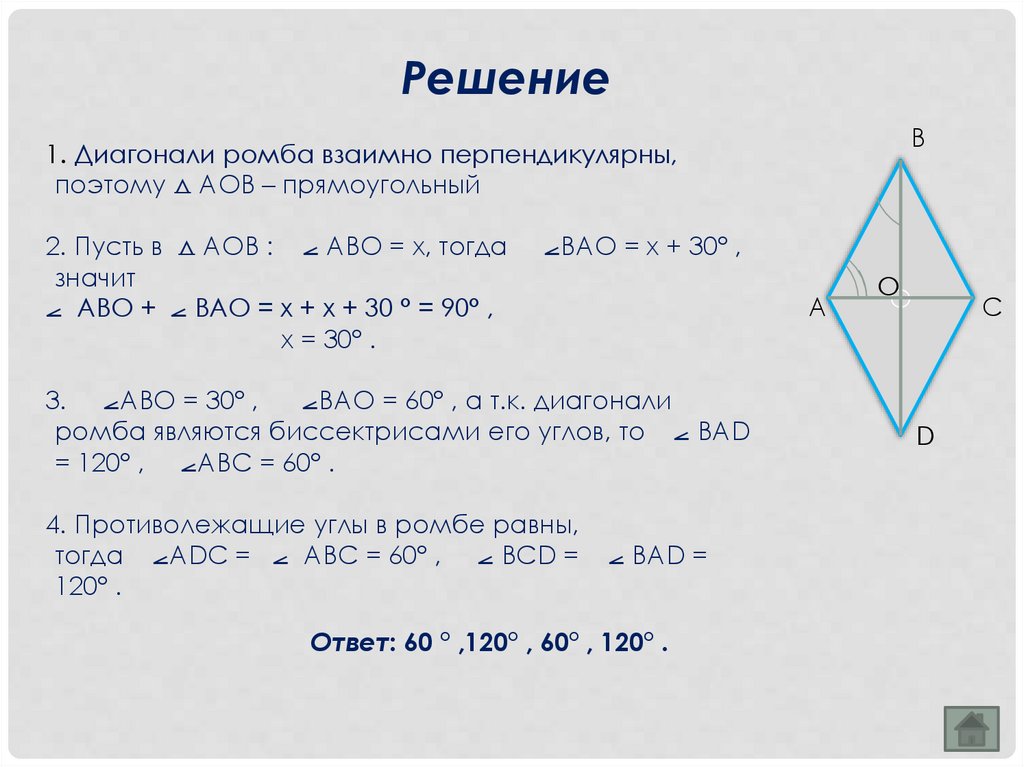
РешениеВ
1. Диагонали ромба взаимно перпендикулярны,
поэтому ⧍ АОВ – прямоугольный
2. Пусть в ⧍ АОВ : ⦟ АВО = х, тогда
значит
⦟ АВО + ⦟ ВАО = х + х + 30 ° = 90° ,
х = 30° .
⦟ВАО = х + 30° ,
А
3. ⦟АВО = 30° ,
⦟ВАО = 60° , а т.к. диагонали
ромба являются биссектрисами его углов, то ⦟ ВАD
= 120° , ⦟АВС = 60° .
4. Противолежащие углы в ромбе равны,
тогда ⦟АDС = ⦟ АВС = 60° , ⦟ ВСD =
120° .
⦟ BAD =
Ответ: 60 ° ,120° , 60° , 120° .
ОО
С
D
20.
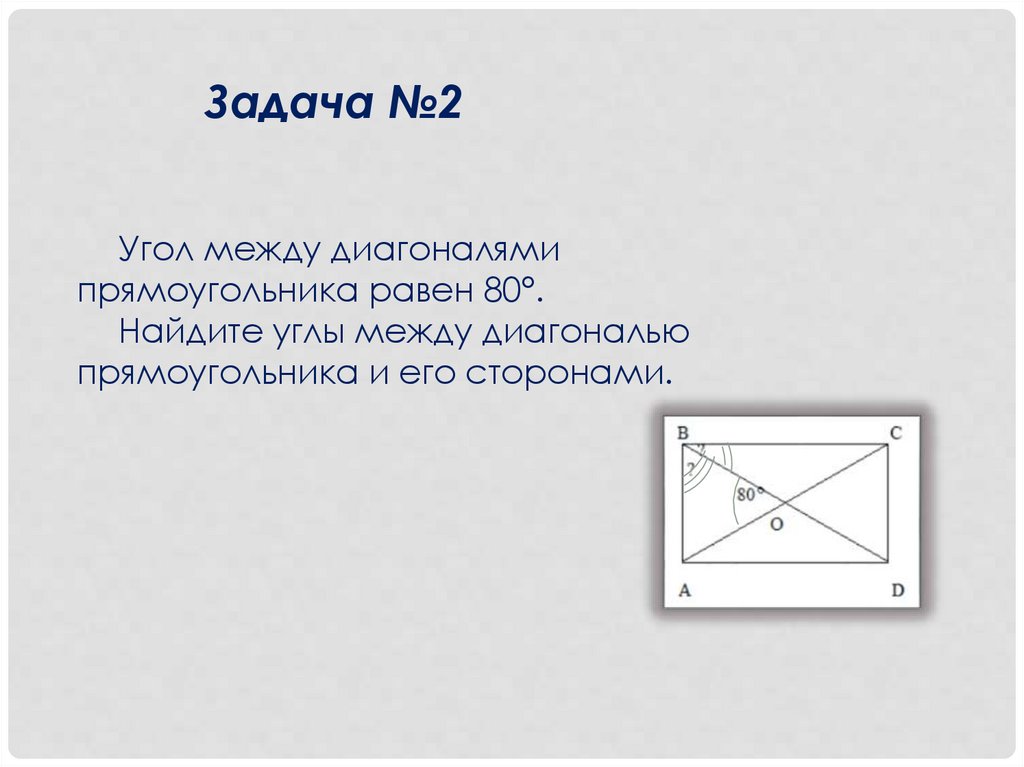
Задача №2Угол между диагоналями
прямоугольника равен 80°.
Найдите углы между диагональю
прямоугольника и его сторонами.
21.
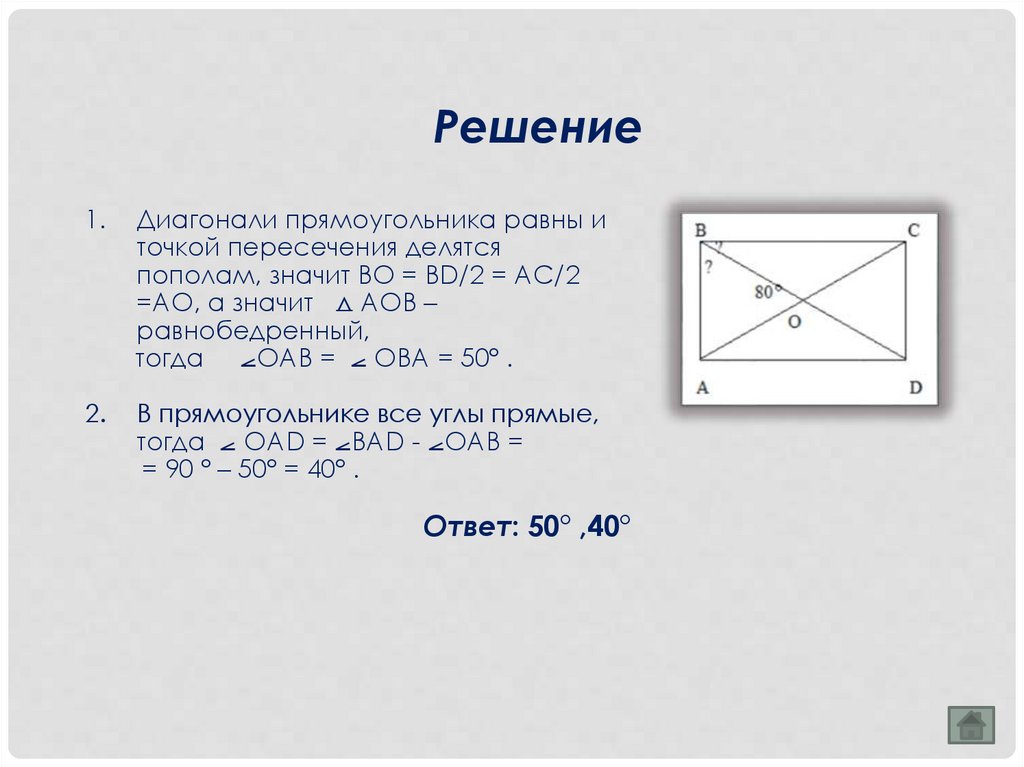
Решение1.
Диагонали прямоугольника равны и
точкой пересечения делятся
пополам, значит ВО = ВD/2 = АС/2
=АО, а значит ⧍ АОВ –
равнобедренный,
тогда ⦟ОАВ = ⦟ ОВА = 50° .
2.
В прямоугольнике все углы прямые,
тогда ⦟ ОАD = ⦟ВАD - ⦟ОАВ =
= 90 ° – 50° = 40° .
Ответ: 50° ,40°
22.
Спасибо за сотрудничествоУдачи








 Математика
Математика








