Похожие презентации:
Свойства логарифмов. 11 класс
1.
Свойства логарифмов11 класс
Учитель математики МКОУ Лисянская СОШ
Деревянкина С. Е.
2.
Логарифмы – это все!Музыка и звуки!
И без них никак нельзя
Обойтись науке!
Н. Будлянская
3.
Повторим логарифмы:1) log a 1
2) log 5 25
3) log a a
4)3log3 7
1
5) log 3
81
6) lg 0,001
7)32 log3 18
loga b
8)a
c
9) log a a
Поставь в соответствие:
1) 2
2) -4
3) 7
4) 0
5) 1
6) С
7) -3
8) b
9) ½
4.
Что такое «Логарифм»?a x b;
х log a b;
a
loga b
b
a>0, a≠1, b>0
Основное
логарифмическое
тождество.
log a a 1;
log a 1 0;
c
log a a c.
Логарифмом положительного числа b по положительному и
отличному от единицы основанию a называют показатель степени, в
которую нужно возвести число a,чтобы получить число b.
4
5.
Логарифмы в музыкеРазве музыкальная гамма не есть
Набор передовых логарифмов?
Английский поэт Э.Брилл
«Представьте, как же неприятно был
поражен мой товарищ, когда я доказал
ему, что, играя по клавишам
современного рояля, он играет,
собственно говоря, на логарифмах…»
N n 2 ( 2)
m 12
p
?
p
log 2 N m
12
N-число колебаний любого тона, m-номер октавы, p-номер ноты октавы,
n-число колебаний самой низкой ноты .
6.
Попробуй объяснить:log 6 9 log 6 4 log 6 4 9 log 6 36 2;
lg 25 lg 4 lg 25 4 lg 100 2;
10
log 5 10 log 5 2 log 5 log 5 5 1;
2
15
1
log 2 15 log 2 30 log 2
log 2 1.
30
2
log 7 25 log 7 52 2 log 7 5
2;
log 7 5
log 7 5
log 7 5
Теорема1.
Теорема2.
Теорема3.
7.
Теорема1: Логарифм произведения двух положительныхчисел равен сумме логарифмов этих чисел:
log a bc log a b log a c.
Доказательство.
Обозначим:
Получаем:
log a b x,
log a c y,
log a bc z.
a x b,
a y c,
a z bc,
Доказать:
z=x+y
b c bc,
ax ay az
a x y a z
x y z.
Пример:
log
1
12
4 log 1 36 log
12
1 2
4
36
log
144
log
(
) 2.
1
1
1
12
12
12 12
8.
Теорема2. Если a, b, c – положительные числа, причем а≠1,то справедливо равенство
b
log a log a b log a c.
c
Докажите самостоятельно.
Пример.
28
1 2
log 1 28 log 1 7 log 1
log 1 4 log 1 ( ) 2.
2
2
2 7
2
2 2
9.
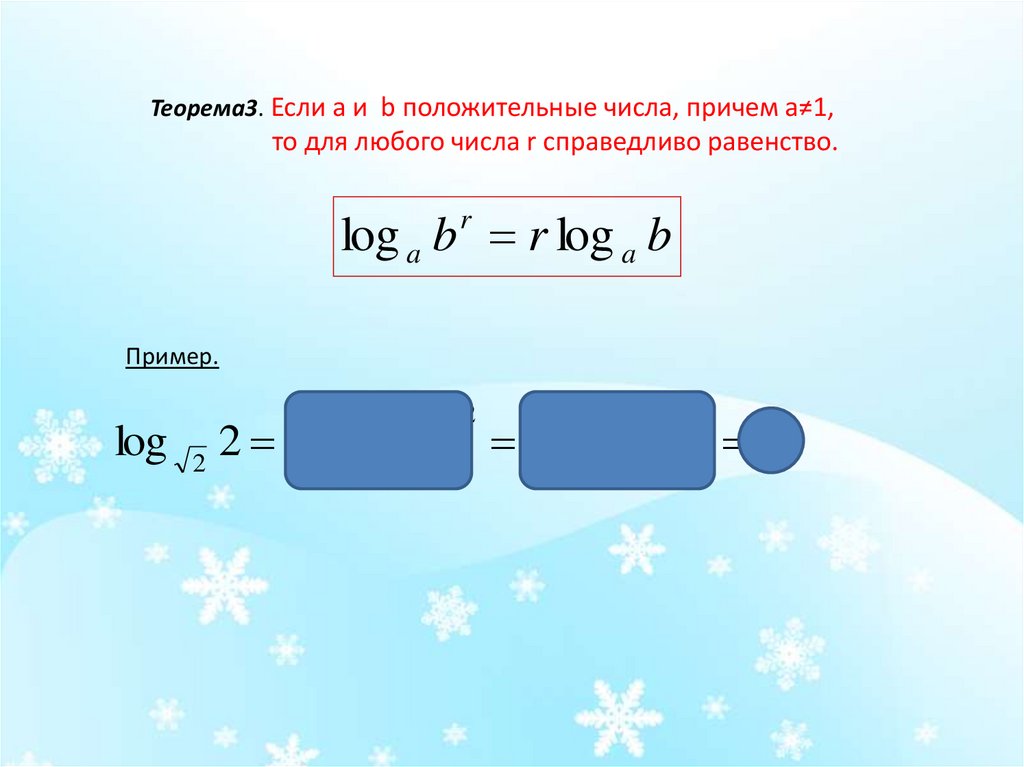
Теорема3. Если a и b положительные числа, причем a≠1,то для любого числа r справедливо равенство.
log a b r log a b
r
Пример.
log
2
2 log
2 2 log
2
2
2
2 2.
10.
Музыка и логарифмы:N n 2 ( 2)
m 12
p
log 2 N m
12
p
Прологарифмируем по основанию 2:
p
12
log 2 N log 2 (n 2 m (12 2 ) p ) log 2 n log 2 2 m log 2 2
p
p
log 2 1 m log 2 2 log 2 2 m .
12
12
p
Номера клавишей рояля
12 представляют собой логарифмы
по основанию2 чисел колебаний (N) соответствующих звуков.
m










 Математика
Математика








