Решение неравенств второй степени с одной переменной. 9 класс

1.

2.

Цели
Предметные
Ввести понятие неравенств второй степени с одной переменной, дать
определение
Познакомить с алгоритмом решения неравенств на основе свойств
квадратичной функции
Сформировать умение решать неравенства данного вида
Метапредметные:
Развивать умение анализировать, выделять главное, обобщать
Развивать навыки самопроверки, самоконтроля, логическое мышление
Развивать навыки культуры речи: умение вести диалог, грамотно говорить,
аргументированно высказывать точку зрения
Личностные:
Формировать навыки общения, умения работать в парах, уважать мнение
каждого
Воспитывать познавательный интерес к предмету, формировать
положительную мотивацию

3. Повторим квадратичную функцию

• * Дайте определение
квадратичной функции.
• * Что представляет собой
график квадратичной функции?
• * Как определить направление
ветвей параболы?

4.

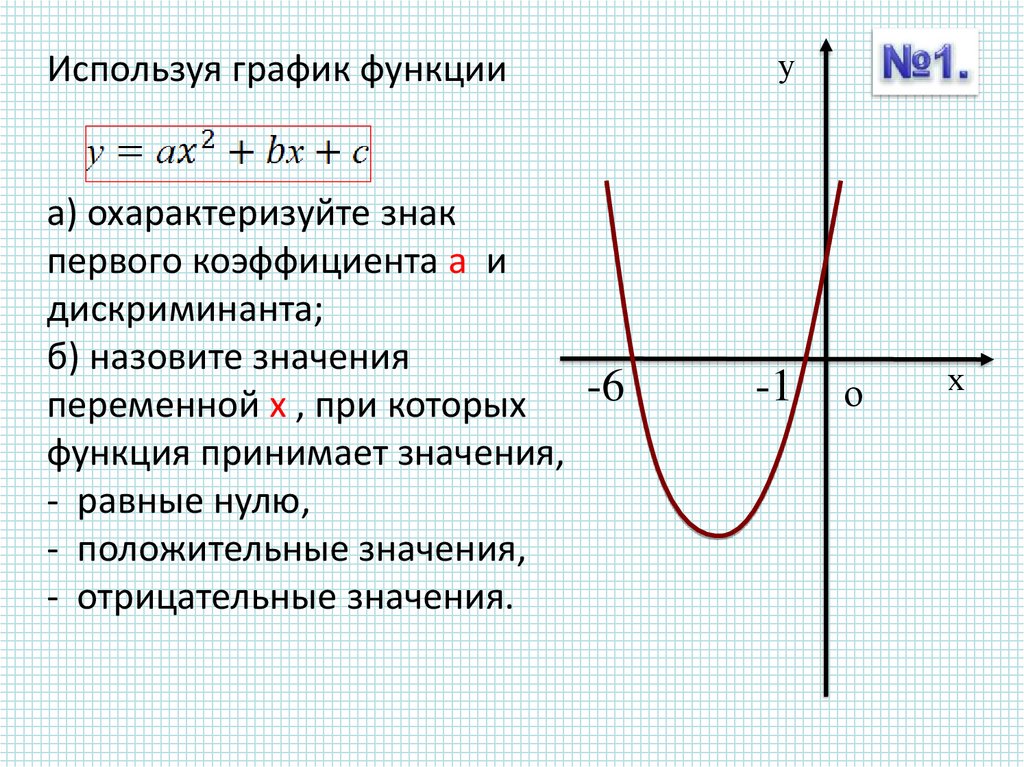
Используя график функции
а) охарактеризуйте знак
первого коэффициента а и
дискриминанта;
б) назовите значения
-6
переменной х , при которых
функция принимает значения,
- равные нулю,
- положительные значения,
- отрицательные значения.
у
-1
о
х

5.

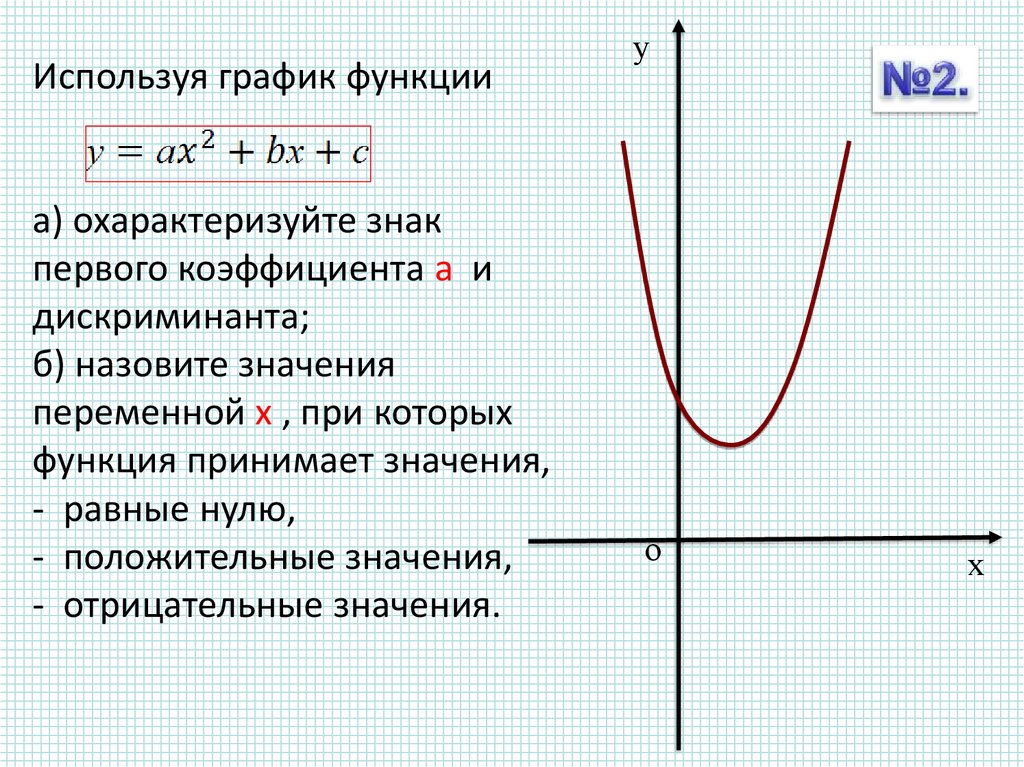
Используя график функции
а) охарактеризуйте знак
первого коэффициента а и
дискриминанта;
б) назовите значения
переменной х , при которых
функция принимает значения,
- равные нулю,
- положительные значения,
- отрицательные значения.
у
о
х

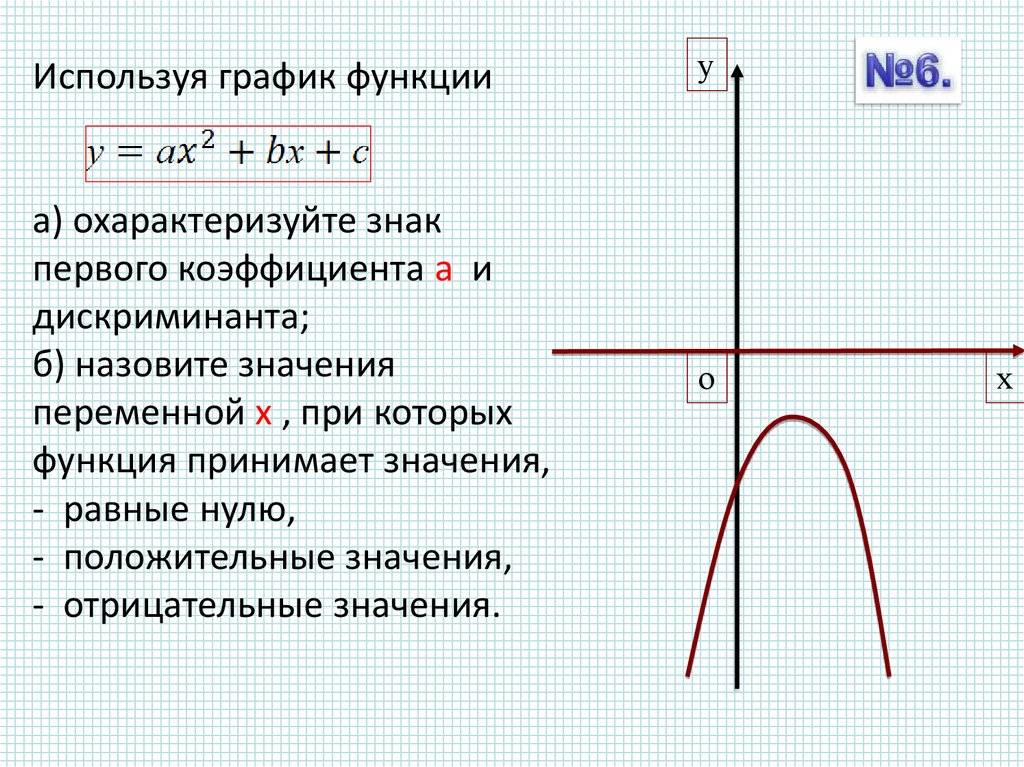
6.

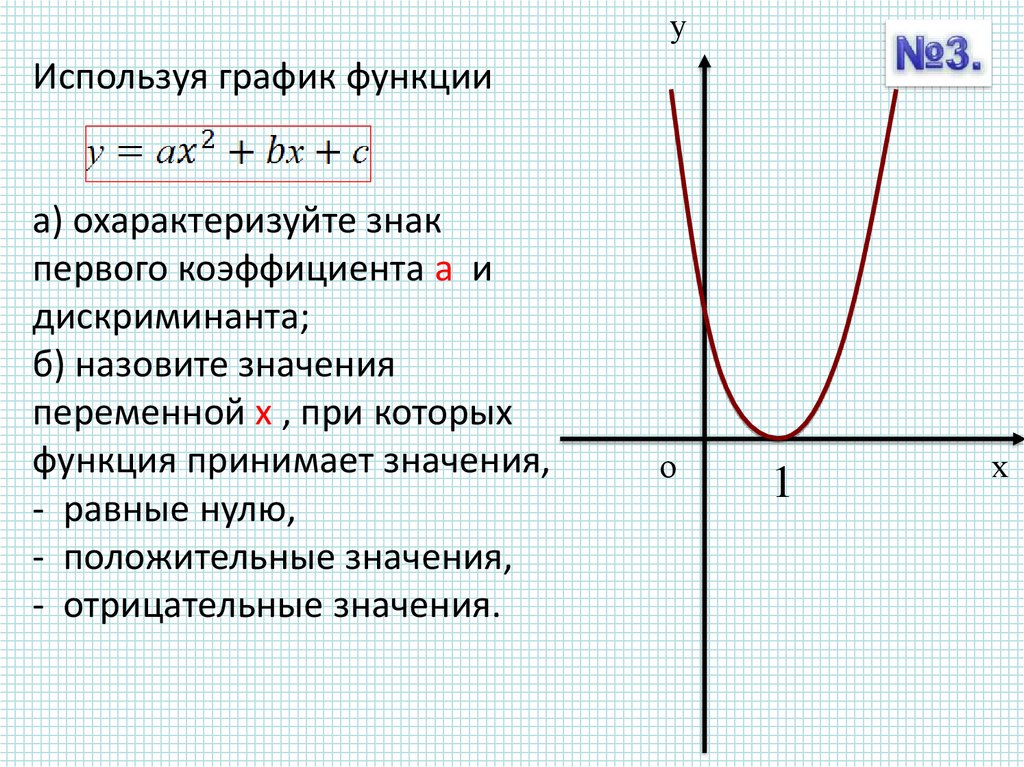
у
Используя график функции
а) охарактеризуйте знак
первого коэффициента а и
дискриминанта;
б) назовите значения
переменной х , при которых
функция принимает значения,
- равные нулю,
- положительные значения,
- отрицательные значения.
о
1
х

7.

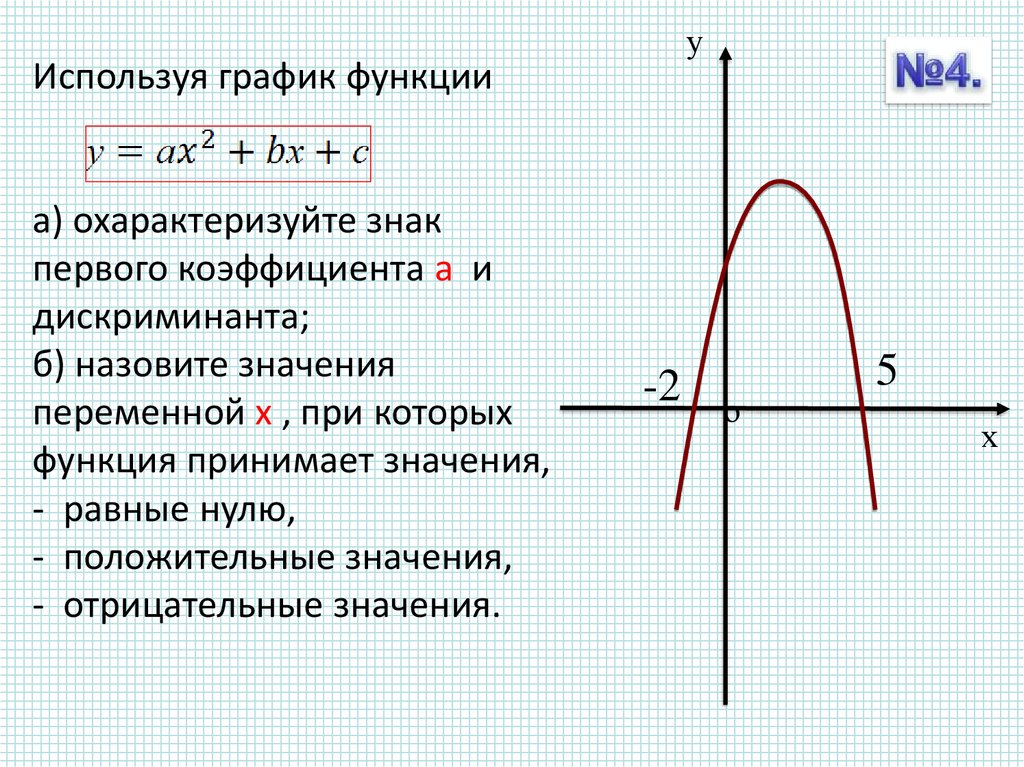
у
Используя график функции
а) охарактеризуйте знак
первого коэффициента а и
дискриминанта;
б) назовите значения
переменной х , при которых
функция принимает значения,
- равные нулю,
- положительные значения,
- отрицательные значения.
-2
о
5
х

8.

у
Используя график функции
а) охарактеризуйте знак
первого коэффициента а и
дискриминанта;
б) назовите значения
переменной х , при которых
функция принимает значения,
- равные нулю,
- положительные значения,
- отрицательные значения.
-3
о
х

9.

Используя график функции
а) охарактеризуйте знак
первого коэффициента а и
дискриминанта;
б) назовите значения
переменной х , при которых
функция принимает значения,
- равные нулю,
- положительные значения,
- отрицательные значения.
у
о
х

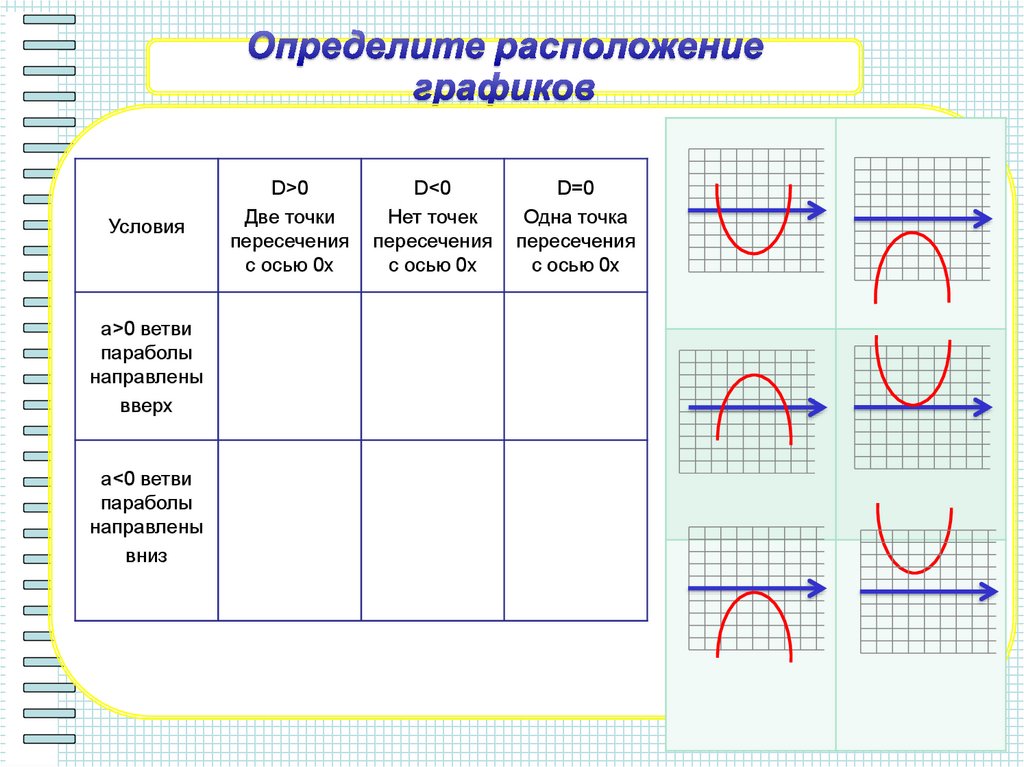
10.

Условия
a>0 ветви
параболы
направлены
вверх
a<0 ветви
параболы
направлены
вниз
D>0
Две точки
пересечения
с осью 0х
D<0
Нет точек
пересечения
с осью 0х
D=0
Одна точка
пересечения
с осью 0х

11.

Неравенства второй степени с одной переменной
Неравенства вида ax2 + bx + c > 0 и ax2 + bx + c < 0,
(ax2 + bx + c ≥ 0; ax2 + bx + c ≤ 0)
где x – переменная, a, b и c – некоторые числа и a ≠ 0, называют
неравенствами второй степени с одной переменной
Решение неравенства
ax2 + bx + c > 0 или ax2 + bx + c < 0
(ax2 + bx + c ≥ 0; ax2 + bx + c ≤ 0)
можно рассматривать как нахождение промежутков, в которых функция
y = ax2 + bx + c принимает положительные или отрицательные значения

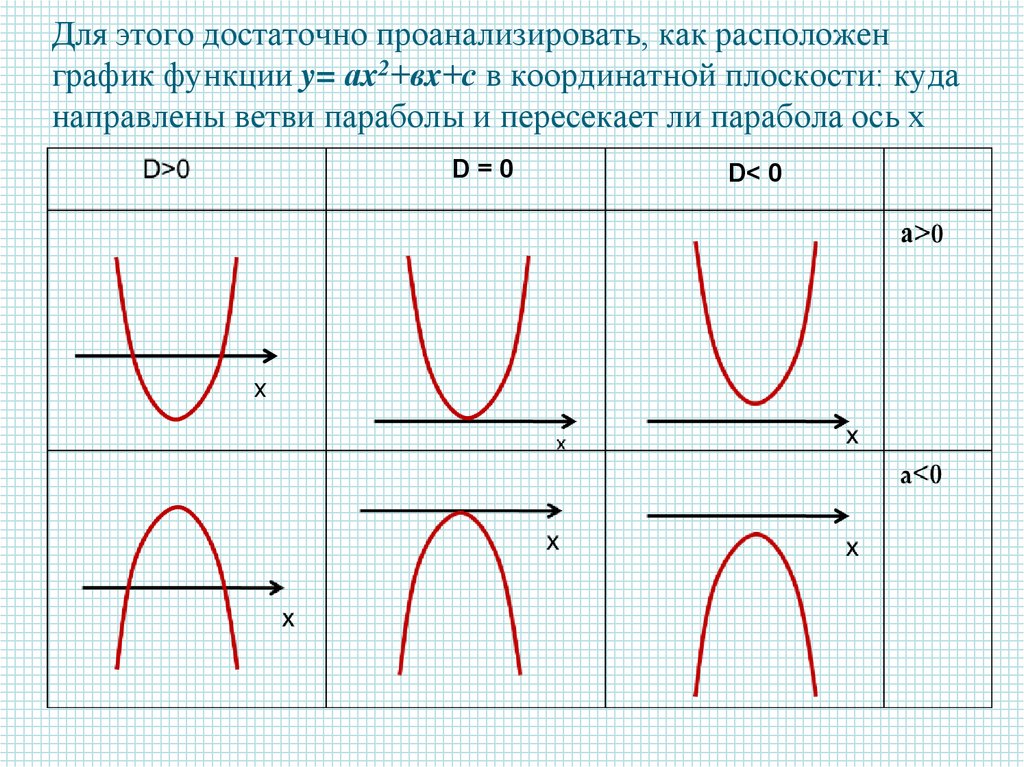
12.

Для этого достаточно проанализировать, как расположен
график функции y= аx2+вx+с в координатной плоскости: куда
направлены ветви параболы и пересекает ли парабола ось х
D=0
x
D< 0

13. Решим неравенство 5х2 + 9х – 2 < 0

Решим неравенство 5х2 + 9х – 2 < 0
• Рассмотрим квадратичную функцию
у = 5х2 + 9х – 2
• Графиком этой функции является парабола,
а = 5 >0 ветви направлены вверх.
Решим уравнение 5х2 + 9х – 2 = 0.
5х2 + 9х – 2 = 0.
D = b2 – 4ac = 92 - 4 5 (-2) = 81 + 40 = =121,
х1
b D
9 11
2
1
2a
10
10
5
x2
b D
9 11
2
2a
10
-2
Ответ:
1
х ( 2; )
5
1
5
x

14.

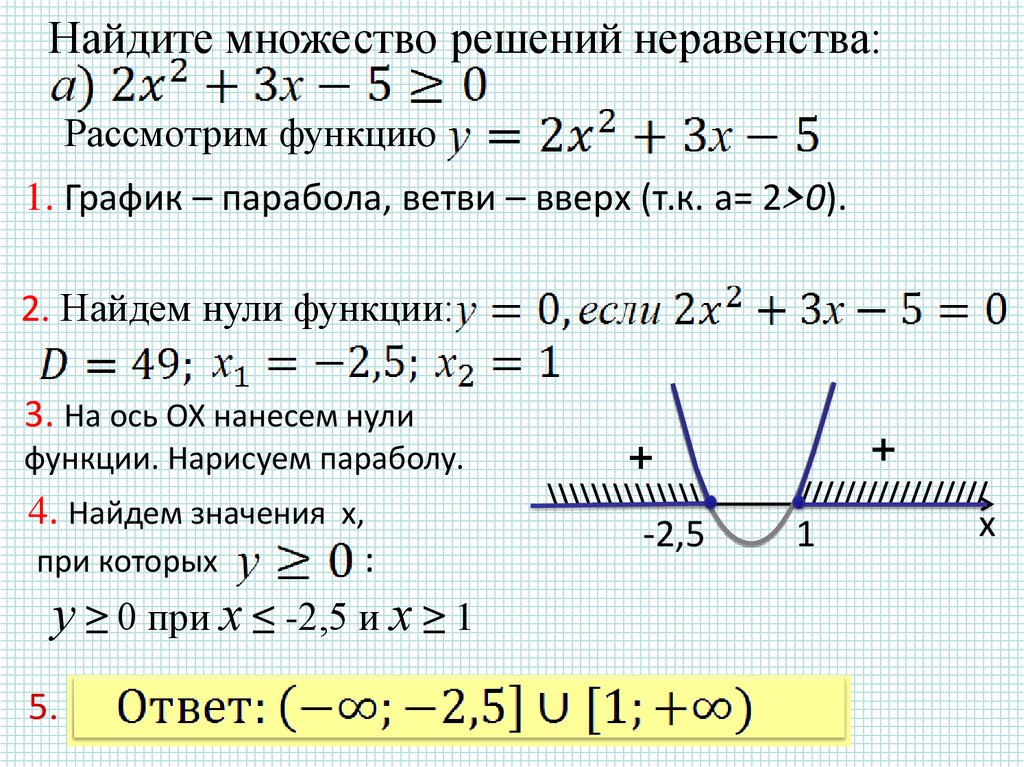
Найдите множество решений неравенства:
Рассмотрим функцию
1. График – парабола, ветви – вверх (т.к. а= 2>0).
2. Найдем нули функции:
3. На ось ОХ нанесем нули
функции. Нарисуем параболу.
4. Найдем значения х,
при которых
:
у ≥ 0 при х ≤ -2,5 и х ≥ 1
5.
+
\\\\\\\\\\\\\\
-2,5
+
/////////////////
1
х

15.

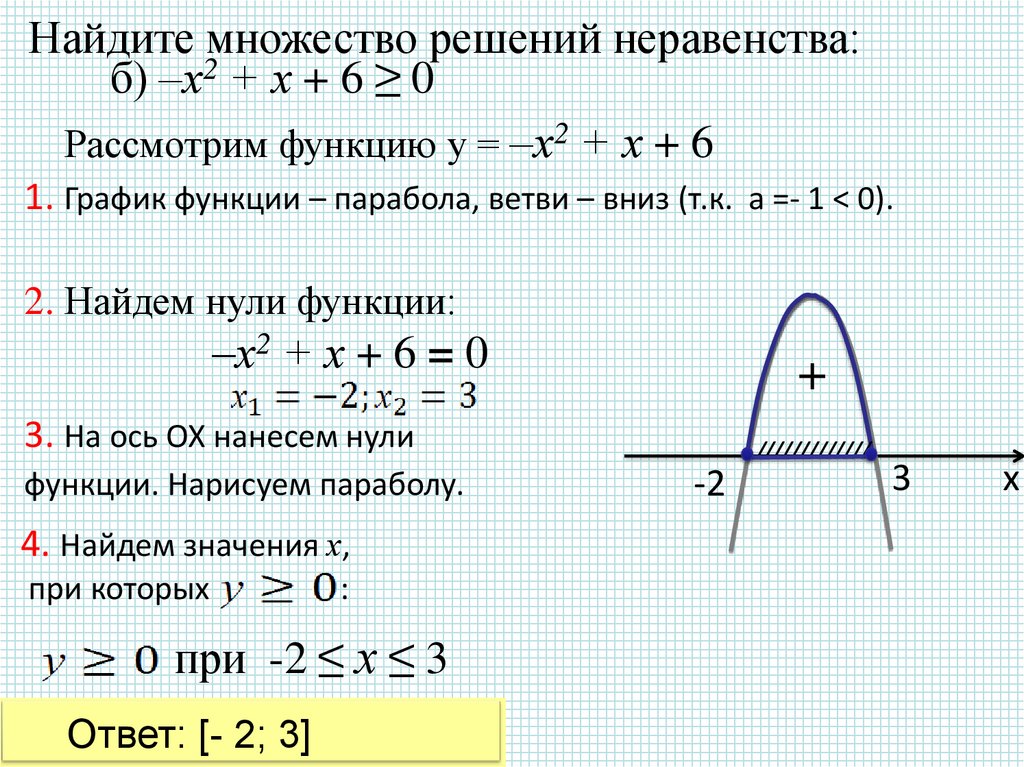
Найдите множество решений неравенства:
б) –х2 + х + 6 ≥ 0
Рассмотрим функцию у = –х2 + х + 6
1. График функции – парабола, ветви – вниз (т.к. а =- 1 < 0).
2. Найдем нули функции:
–х2 + х + 6 = 0
+
3. На ось ОХ нанесем нули
функции. Нарисуем параболу.
4. Найдем значения х,
при которых
:
при -2 ≤ х ≤ 3
Ответ: [- 2; 3]
/////////////
-2
3
х

16.

Алгоритм решения неравенств вида
ax2+bx+c>0 и ax2+bx+c<0
Рассмотреть функцию
1. График функции – парабола,
ветви направлены вверх (т.к. а>0) или вниз (т.к.
2. Найти нули функции.
3. На ось ОХ нанести нули функции.
Построить эскиз графика.
4. Найти значения переменной х, при которых
функция принимает нужные значения.
5. Записать ответ.
).

17.

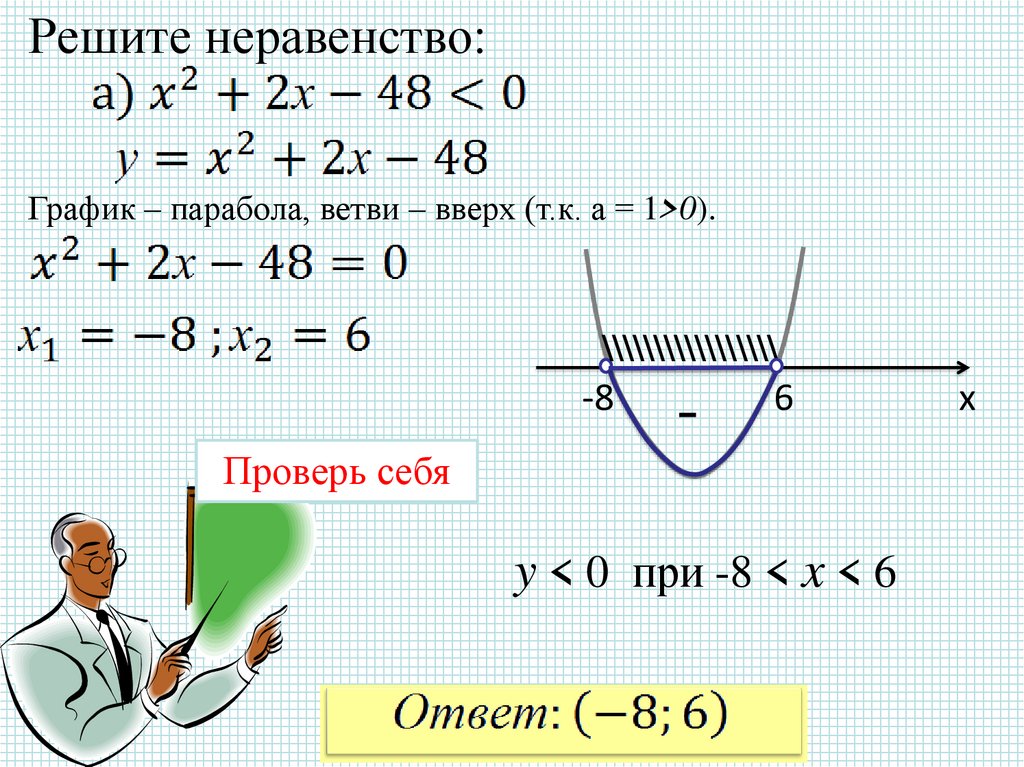
Решите неравенство:
График – парабола, ветви – вверх (т.к. а = 1>0).
\\\\\\\\\\\\\\\\\
-8
-
6
Проверь себя
y < 0 при -8 < x < 6
х

18.

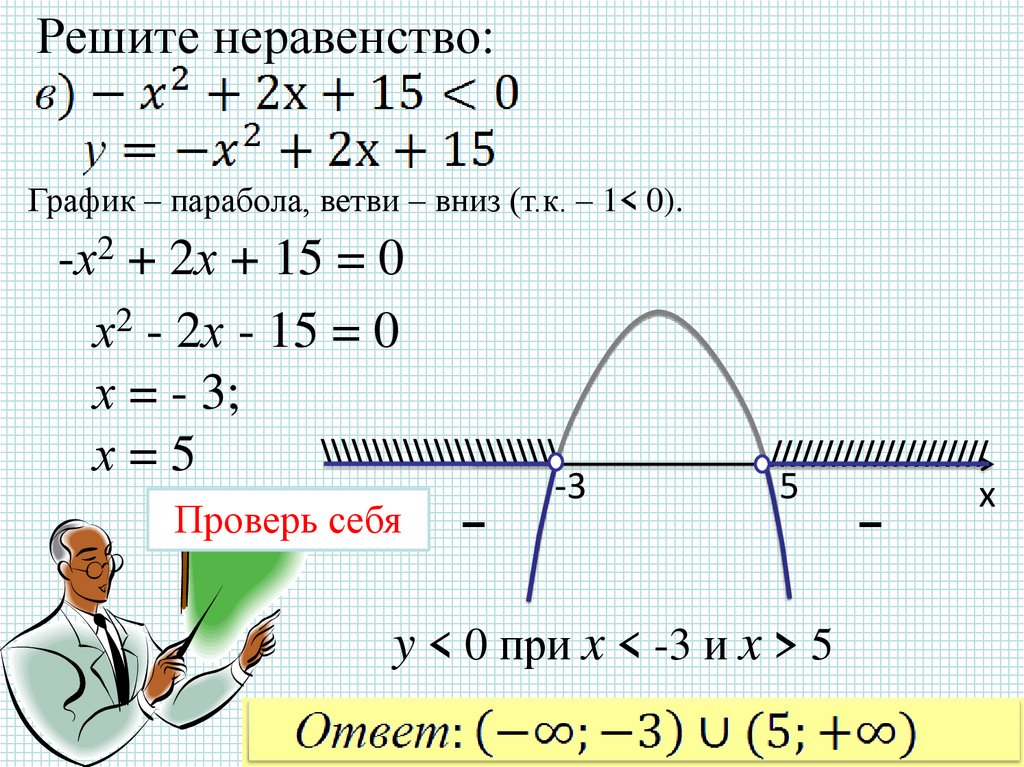
Решите неравенство:
График – парабола, ветви – вниз (т.к. – 1< 0).
-х2 + 2х + 15 = 0
х2 - 2х - 15 = 0
х = - 3;
\\\\\\\\\\\\\\\\\\\\\\\
х=5
-3
Проверь себя -
/////////////////////
5
y < 0 при x < -3 и x > 5
-
х

19.

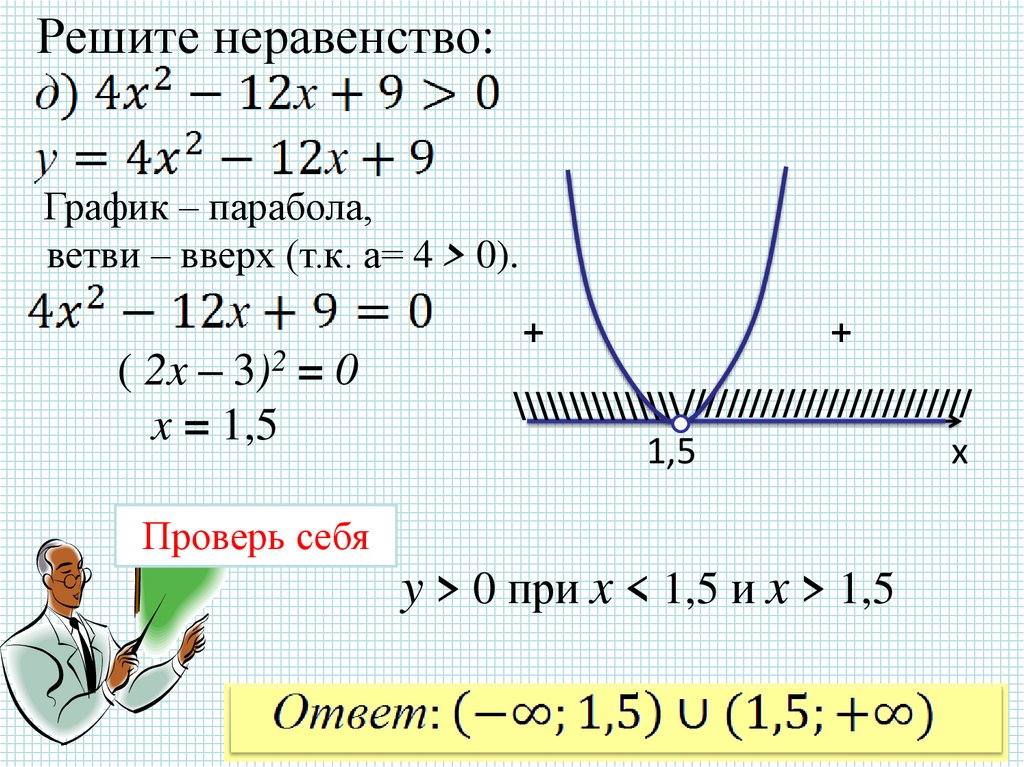
Решите неравенство:
График – парабола,
ветви – вверх (т.к. а= 4 > 0).
( 2x – 3)2 = 0
x = 1,5
+
+
\\\\\\\\\\\\\\\ //////////////////////////
1,5
х
Проверь себя
y > 0 при x < 1,5 и x > 1,5

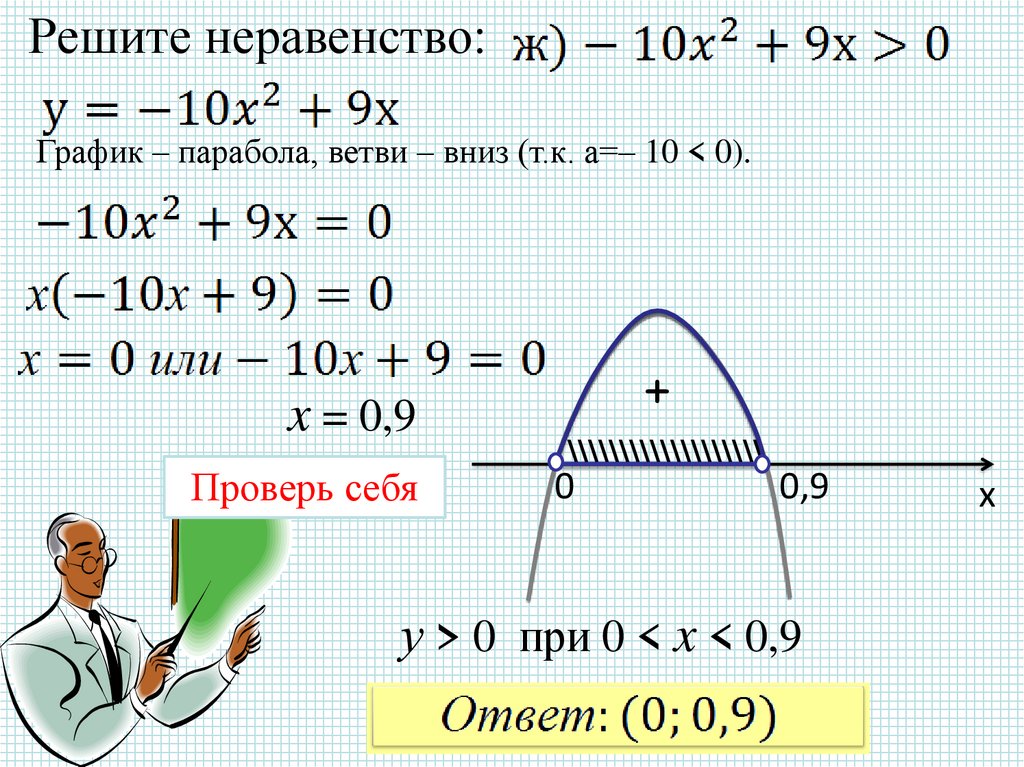
20.

Решите неравенство:
График – парабола, ветви – вниз (т.к. а=– 10 < 0).
x = 0,9
Проверь себя
+
\\\\\\\\\\\\\\\\\\\
0
0,9
у > 0 при 0 < x < 0,9
х

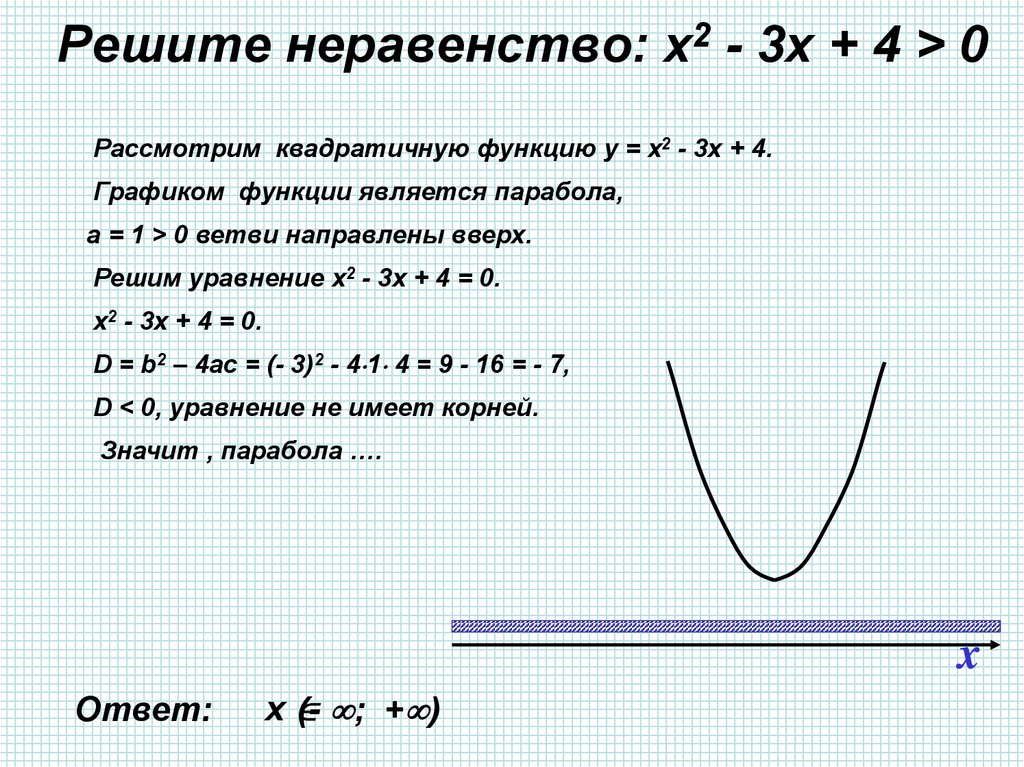
21. Решите неравенство: х2 - 3х + 4 > 0

Решите неравенство: х2 - 3х + 4 > 0
Рассмотрим квадратичную функцию у = х2 - 3х + 4.
Графиком функции является парабола,
а = 1 > 0 ветви направлены вверх.
Решим уравнение х2 - 3х + 4 = 0.
х2 - 3х + 4 = 0.
D = b2 – 4ac = (- 3)2 - 4 1 4 = 9 - 16 = - 7,
D < 0, уравнение не имеет корней.
Значит , парабола ….
x
Ответ:
х
(- ; + )

22. Решим неравенство: х2 - 4х + 4  0

Решим неравенство: х2 - 4х + 4 0
Рассмотрим квадратичную функцию …
Графиком функции является …,
а= ……
ветви направлены ….
Решим уравнение … .
х2 - 4х + 4 = 0.
D = b2 – 4ac = (- 4)2 - 4 1 4 = 16 - 16 = 0,
D = 0, уравнение имеет 1 корень.
х=
2
2
Ответ:
х=2
Ответ: ?
x

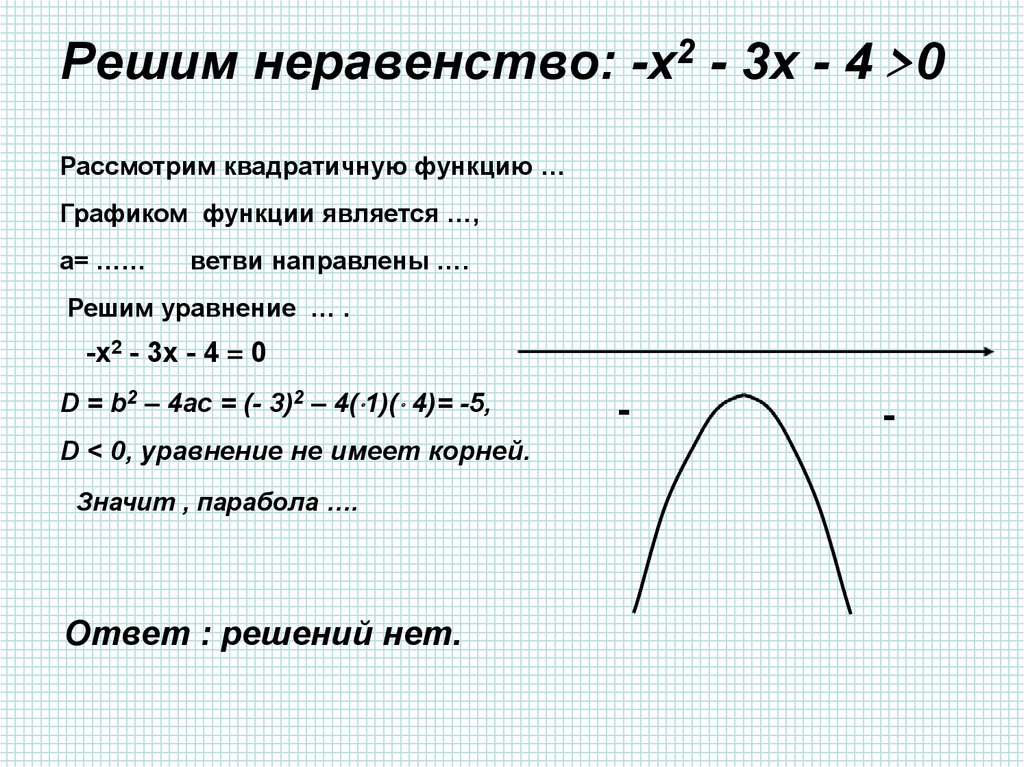
23.

Решим неравенство: -х2 - 3х - 4 >0
Рассмотрим квадратичную функцию …
Графиком функции является …,
а= ……
ветви направлены ….
Решим уравнение … .
-х2 - 3х - 4 = 0
D = b2 – 4ac = (- 3)2 – 4( 1)( 4)= -5,
D < 0, уравнение не имеет корней.
Значит , парабола ….
Ответ : решений нет.
-
-

24.

№ 306 (г, д, е), у доски № 305.
Д/з № 306(а,б,в), № 307.
Выучить алгоритм решения неравенств
второй степени.