Решение неравенств второй степени с одной переменной

1.

Учитель математики
Сулейманова Алие Рустэмовна

2.

3.

Используя график функции
а) охарактеризуйте знак
первого коэффициента а и
дискриминанта;
б) назовите значения
-6
переменной х , при которых
функция принимает значения,
- равные нулю,
- положительные значения,
- отрицательные значения.
у
-1
о
х

4.

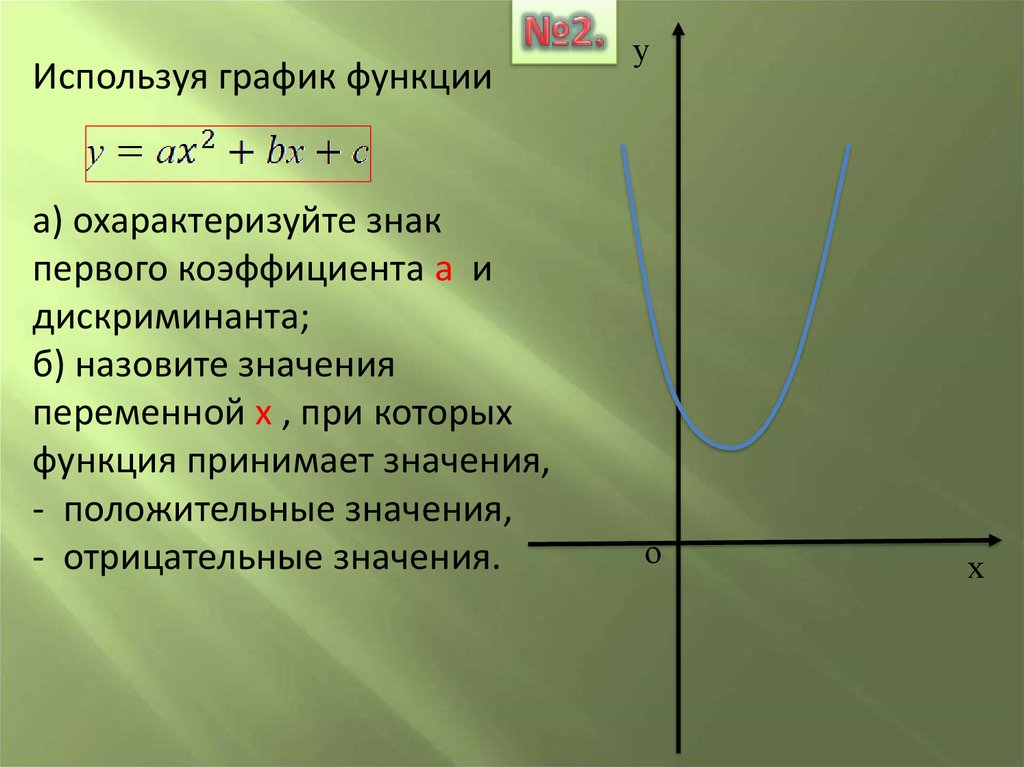
Используя график функции
а) охарактеризуйте знак
первого коэффициента а и
дискриминанта;
б) назовите значения
переменной х , при которых
функция принимает значения,
- положительные значения,
- отрицательные значения.
у
о
х

5.

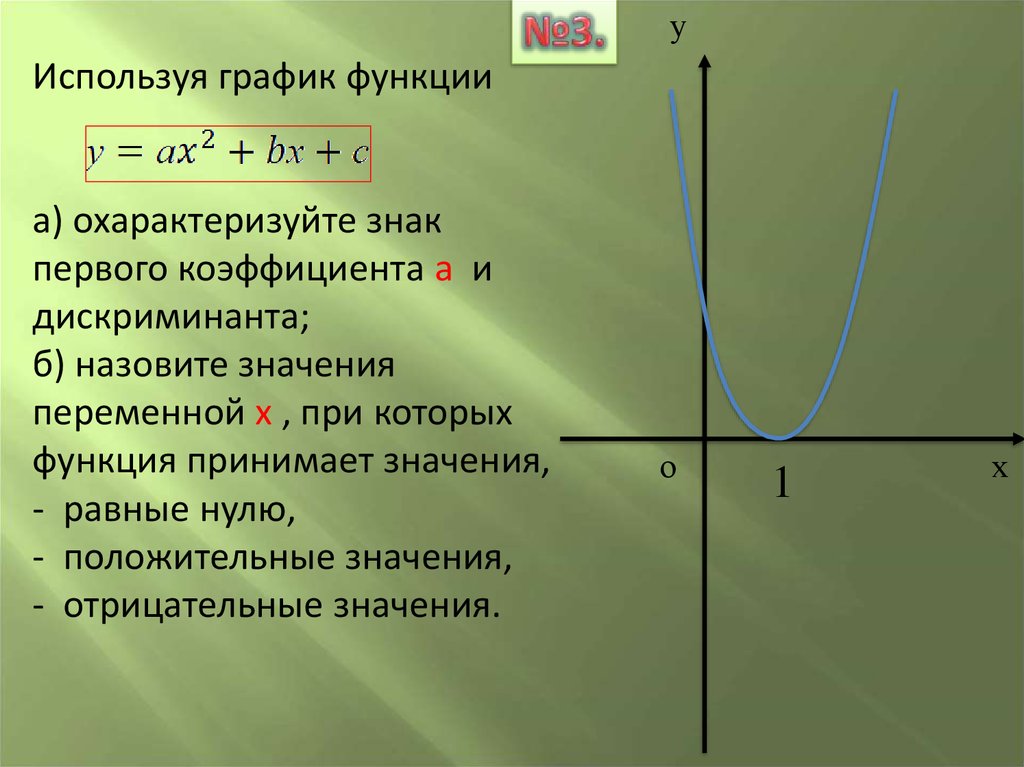
у
Используя график функции
а) охарактеризуйте знак
первого коэффициента а и
дискриминанта;
б) назовите значения
переменной х , при которых
функция принимает значения,
- равные нулю,
- положительные значения,
- отрицательные значения.
о
1
х

6.

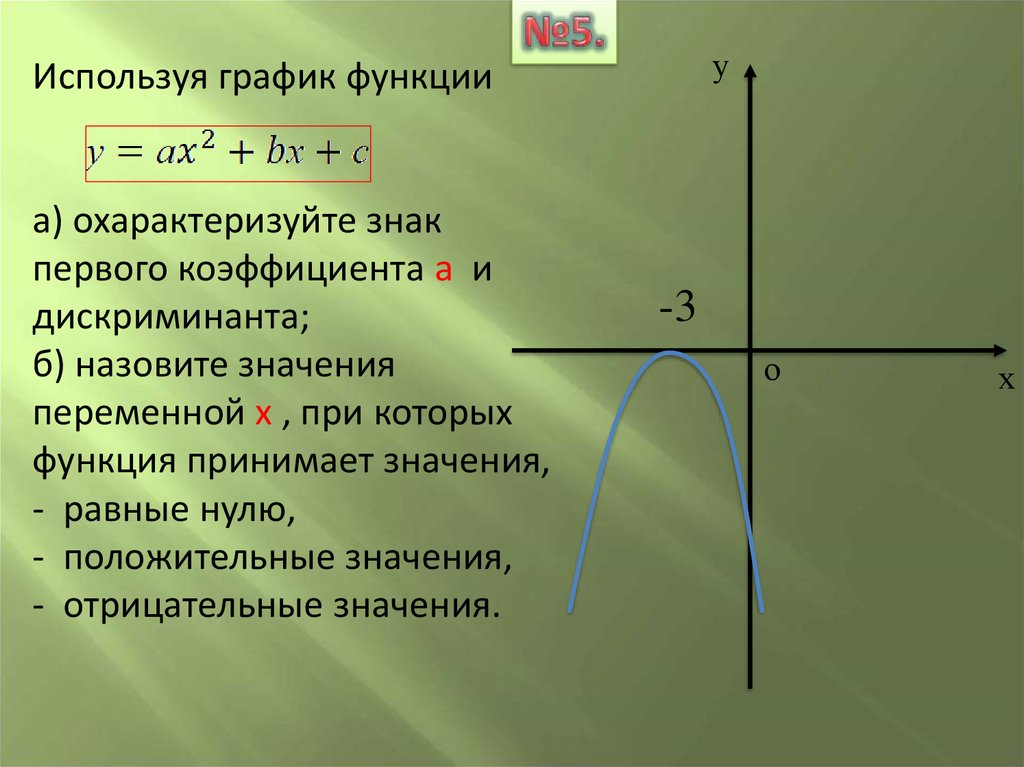
у
Используя график функции
а) охарактеризуйте знак
первого коэффициента а и
дискриминанта;
б) назовите значения
переменной х , при которых
функция принимает значения,
- равные нулю,
- положительные значения,
- отрицательные значения.
-2
о
5
х

7.

у
Используя график функции
а) охарактеризуйте знак
первого коэффициента а и
дискриминанта;
б) назовите значения
переменной х , при которых
функция принимает значения,
- равные нулю,
- положительные значения,
- отрицательные значения.
-3
о
х

8.

Используя график функции
у
а) охарактеризуйте знак
первого коэффициента а и
дискриминанта;
б) назовите значения
переменной х , при которых
функция принимает значения,
- положительные значения,
- отрицательные значения.
о
х

9.

Неравенства вида
aх2 + bх + с > 0 и
aх2 + bх + с < 0
где х - переменная,
а, в, с –некоторые числа,
причем
,
называют неравенствами
второй степени с одной переменной.

10.

Алгоритм решения неравенств вида
ax2+bx+c>0 и ax2+bx+c<0
1. Рассмотрим функцию
2. Графиком функции является парабола ,
ветви которой направлены вверх (т.к. а>0)
/или вниз (т.к.
) /.
3. Найдем нули функции.
4. На область определения функции нанесем
нули функции. Нарисуем параболу.
5. Найдем значения переменной х, при которых
у >0 /или у 0/.

11.

№305(а,б)
№304(а,в,д,ж)
№307(а)
№308(а,в,г)

12.

Найдите множество
решений неравенства:
1. Рассмотрим функцию
2. Графиком функции является парабола , ветви
которой направлены вверх (т.к. 2>0).
3. Найдем нули функции:
4. На область определения
функции нанесем нули функции.
\\\\\\\\\\\\\\\\
Нарисуем параболу.
5. Найдем значения
переменной х, при которых
-2,5
/////////////////
1
х

13.

Найдите множество
решений неравенства:
1. Рассмотрим функцию
2. Графиком функции является парабола , ветви ее
направлены вниз (т.к.
).
3. Найдем нули функции:
4. На область определения
функции нанесем нули
Функции. Нарисуем параболу.
5. Найдем значения переменной
х, при которых
///////////
-2
3
х

14.

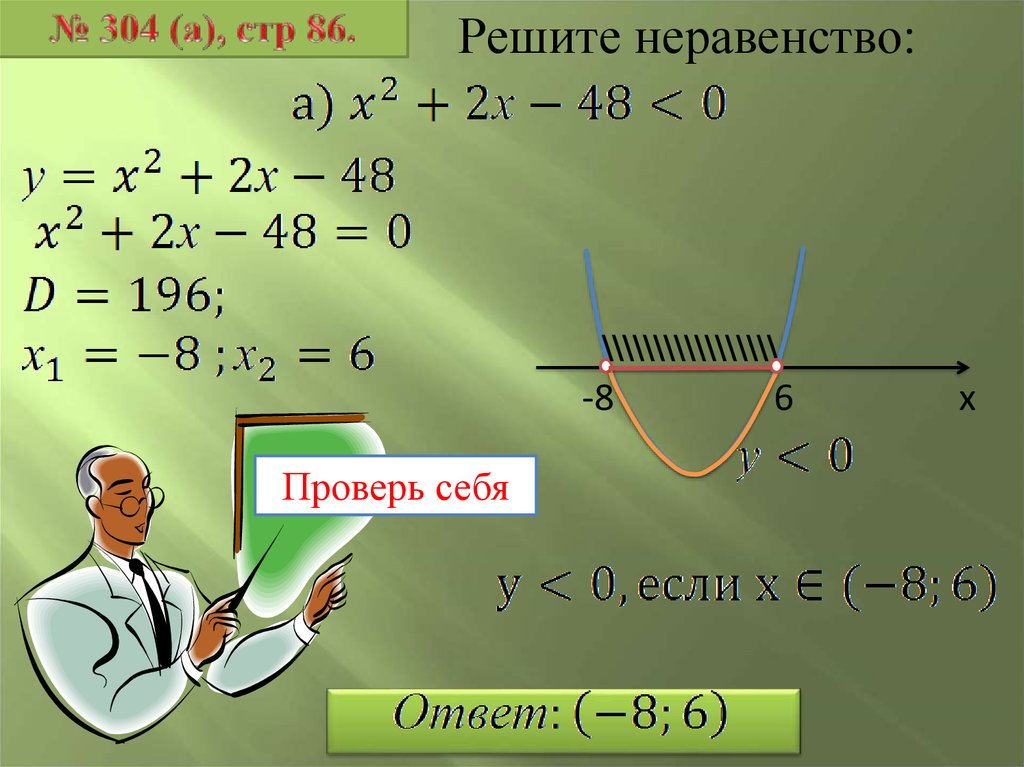
Решите неравенство:
\\\\\\\\\\\\\\\\\
-8
Проверь себя
6
х

15.

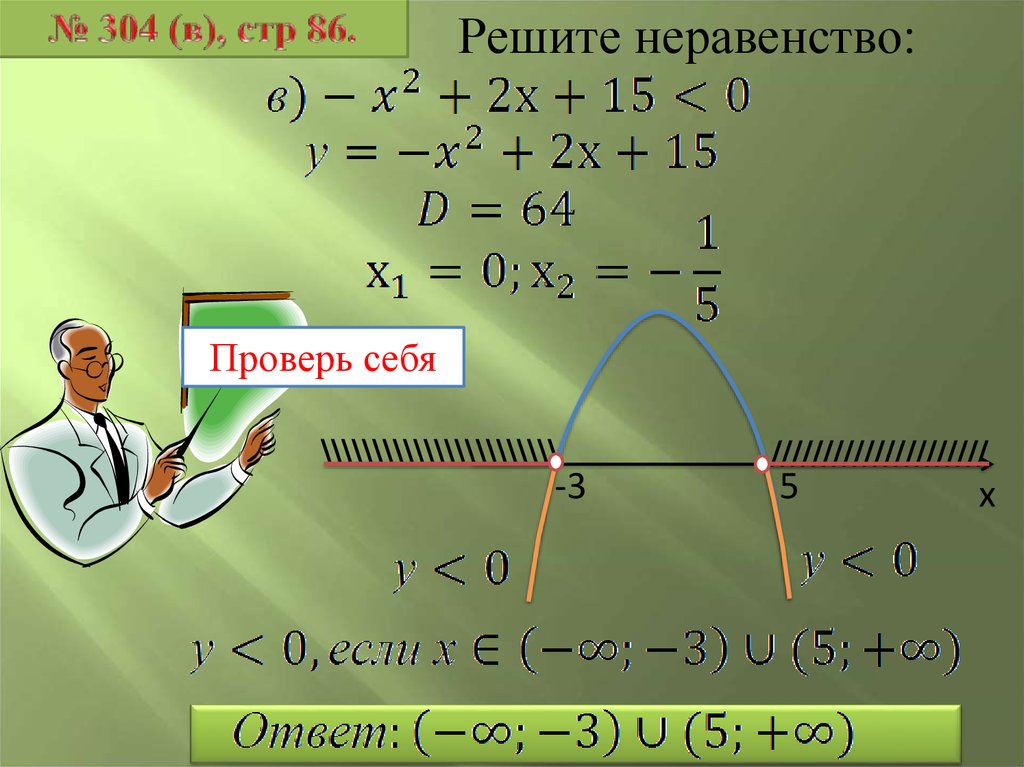
Решите неравенство:
Проверь себя
\\\\\\\\\\\\\\\\\\\\\\\
-3
/////////////////////
5
х

16.

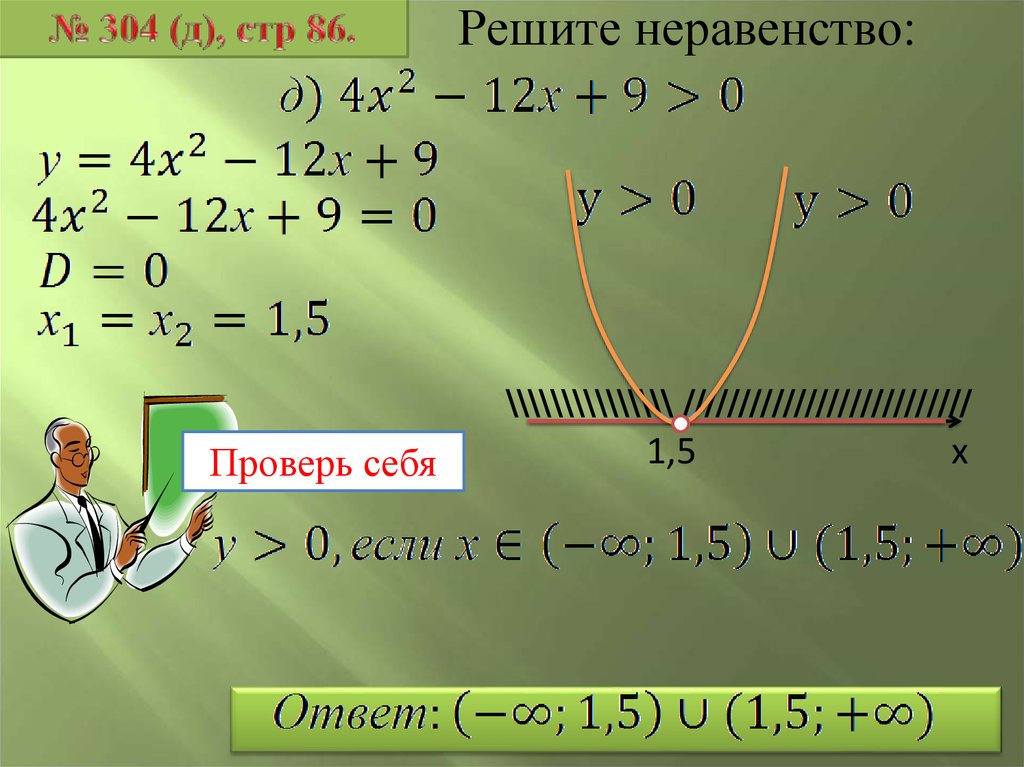
Решите неравенство:
Проверь себя
\\\\\\\\\\\\\\\ //////////////////////////
1,5
х

17.

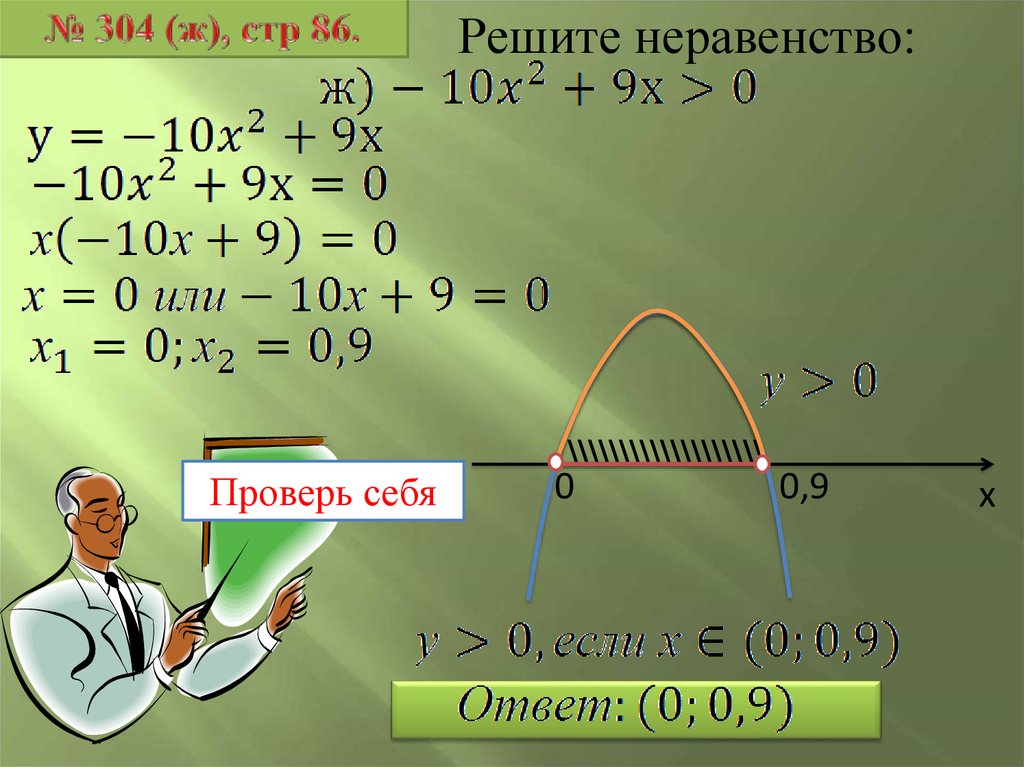
Решите неравенство:
Проверь себя
\\\\\\\\\\\\\\\\\\\
0
0,9
х

18.

Найдите, при каких значениях х трехчлен:
принимает положительные значения.
Проверь себя
Решение:
\\\\\\\\\\\\\
-1,5
/////////////
-1
х

19.

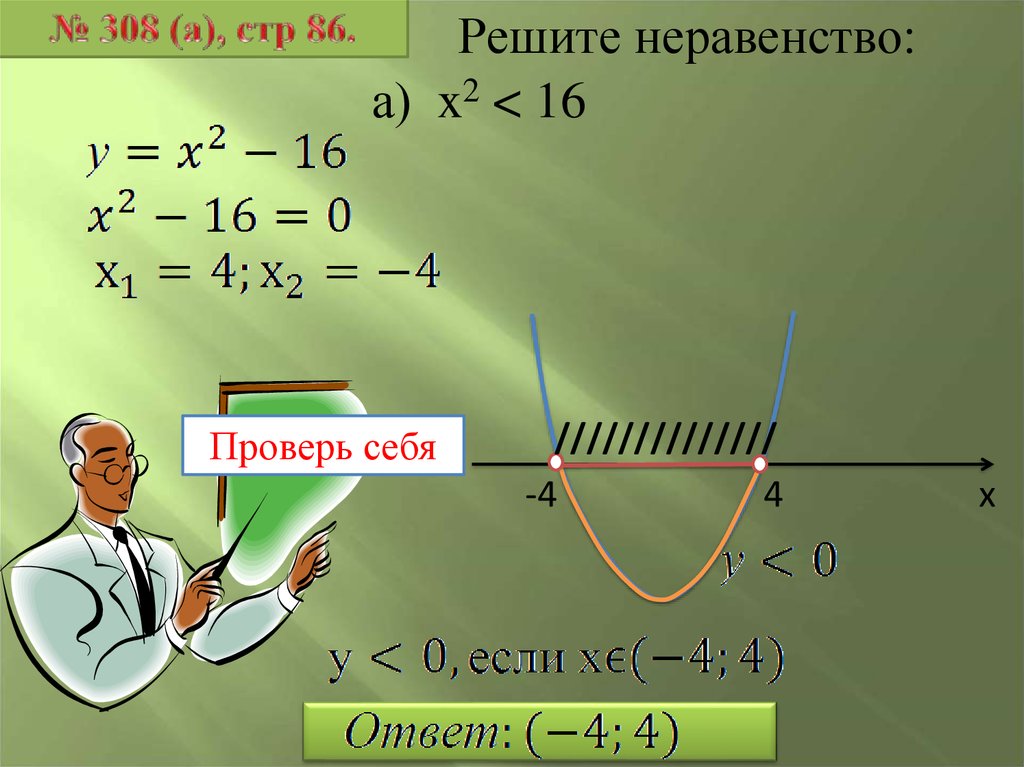
Решите неравенство:
а) x2 < 16
Проверь себя
//////////////
-4
4
х

20.

Решите неравенство:
Проверь себя
\\\\\\\\\\\\\\\
-3
//////////////
3
х

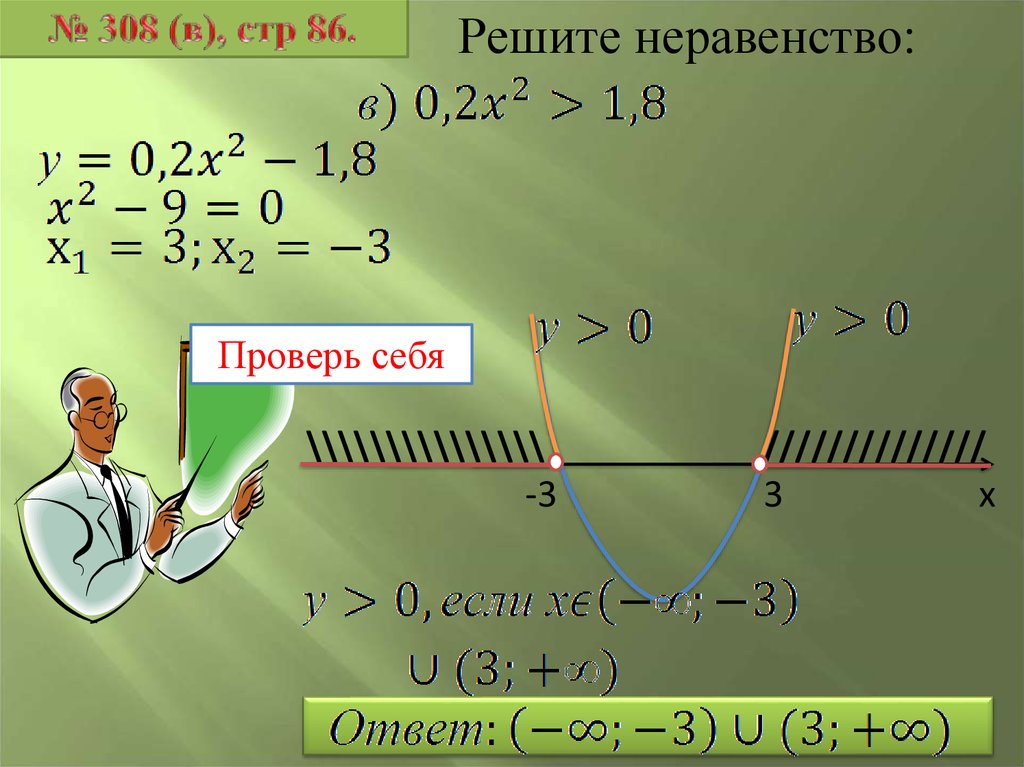
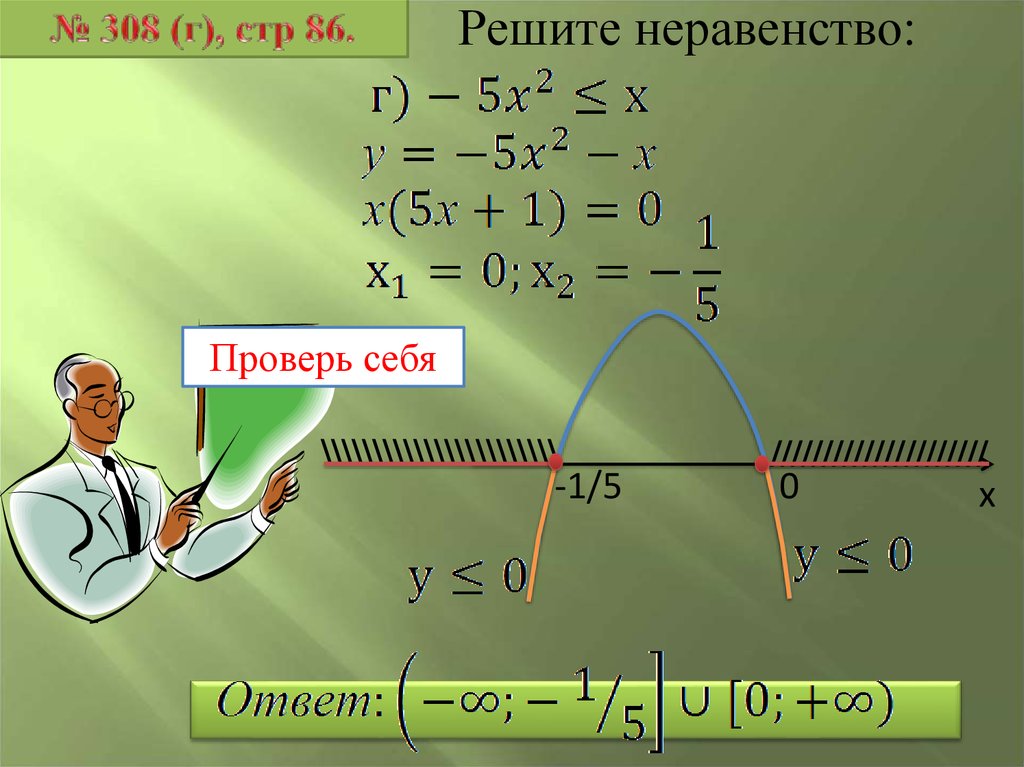
21.

Решите неравенство:
Проверь себя
\\\\\\\\\\\\\\\\\\\\\\\
-1/5
/////////////////////
0
х

22.

23.

•п. 14, стр 83-85
•вопрос 1, стр 93
•№ 304(б,з), 305(в),310(б);буклеты