Тела вращения

1.

ЦИЛИНДР
КОНУС
ШАР
1. ЦИЛИНДР
2. S И V ЦИЛ.
3. КОНУС
4. S И V КОН.
5.УСЕЧ. КОН.
6.СФЕРА И ШАР
7.S СФ.И V Ш.
8.УРАВНЕН. СФ.
9.Ш.В ТЕЛАХ ВР.
10.ТЕЛА ВР.В Ш.
ВЫХОД

2. ЦИЛИНДР

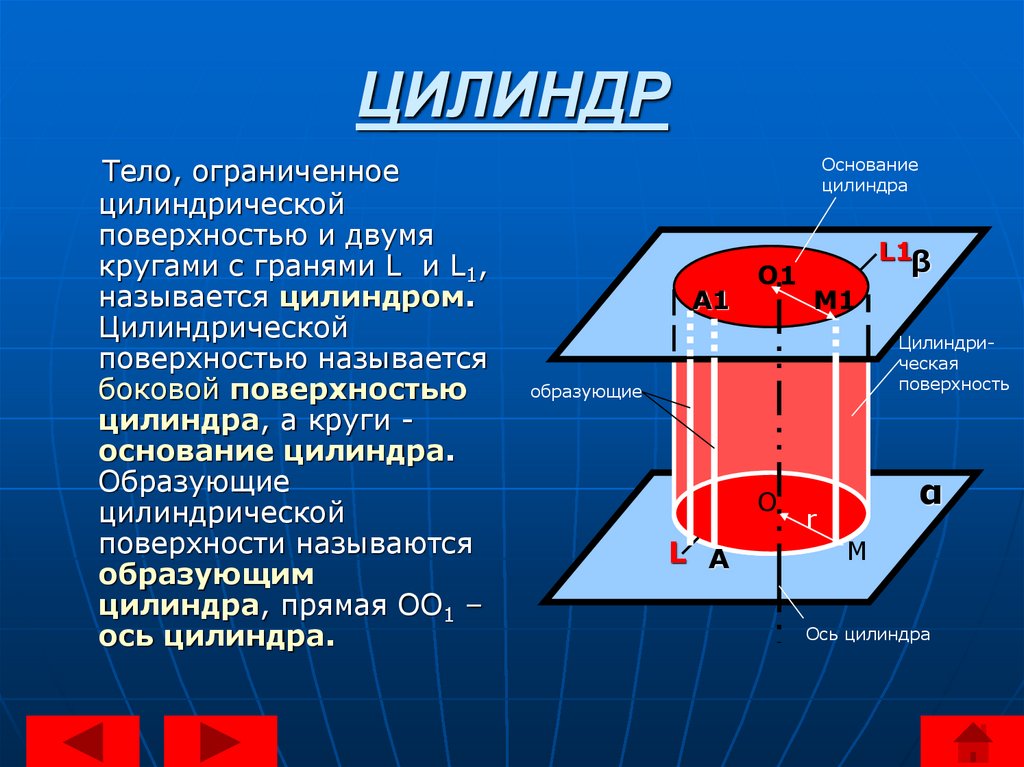
Тело, ограниченное
цилиндрической
поверхностью и двумя
кругами с гранями L и L1,
называется цилиндром.
Цилиндрической
поверхностью называется
боковой поверхностью
цилиндра, а круги основание цилиндра.
Образующие
цилиндрической
поверхности называются
образующим
цилиндра, прямая OO1 –
ось цилиндра.
Основание
цилиндра
A1
O1
L1β
M1
Цилиндрическая
поверхность
образующие
O
L A
α
r
M
Ось цилиндра

3. Площадь поверхности и объем цилиндра

Площадь боковой
поверхности цилиндра
А1
O1
А
O
Sбок =2∏rh
высота
Площадь цилиндра
Sцил=2∏r(r+h)
Объем цилиндра
V=Sосн×h
V=∏r2h
Основание
цилиндра

4. КОНУС

Конусом называется
тело, ограниченное
конической
поверхностью и
кругом. Образующие
конической
поверхности РА, РВ,
и тд.– образующие
конуса. Основание
конуса- круг. Р –
вершина конуса. РО
– высота конуса.
Р
Вершина
конуса
образующие
высота
А
О
Основание
конуса
В

5. Площадь поверхности и объем конуса

Площадь боковой
поверхности конуса
Sбок=∏rL
L-образующая
r-радиус основания
Площадь полной
поверхности конуса
Р
h
Sкон=∏r(L+r)
Объем конуса
∏r2h
V=1/3
V=1/3 Sосн×h
А
L
r
О
В

6. Усеченный конус.

площадь боковой
поверхности
усеченного конуса
Sбок=∏L(r+r1)
r,r1 – радиусы
оснований
объем усеченного
конуса
V=1/3h(S+S1+√SS1)
S,S1- площади
оснований
О,О1- высота h
r1
O1
r
O
L

7. Сфера и шар.

Сферой называется
поверхность, состоящая
из всех точек
пространства,
расположенных на
данном расстоянии от
данной точки. Данная
точка – центр сферы
(точка О), данное
расстояние – радиус
сферы r. Тело,
ограниченное сферой,
называется шаром.
Центр, радиус сферы- это
центр и радиус шара.
r
r
O

8. Площадь сферы и объем шара

Площадь сферы
S=4∏r2
Объем шара
V=4/3 ∏r3
r- радиус шара
r
r
O

9. Уравнение сферы

Уравнение сферы
радиуса R с центром
С(X0;Y0;Z0) в
прямоугольной
системе координат
имеет вид
(X-X0)²+(Y-Y0)²+(ZZ0)²=R²
M(X;Y;Z) –
произвольная точка
сферы
Z
M
C
O
X
Y

10. Шар, вписанный в тела вращения

а)Сфера вписана в
цилиндр, если она
касается оснований
цилиндра и каждой
его образующей.
б)Сфера вписана в
конус, если она
касается основания
конуса и каждой его
образующей.
а)
б)

11. Тела вращения, вписанные в шар

а)цилиндр вписан в
сферу, если
основания цилиндра
являются сечениями
сферы
б) конус вписан в
сферу, если вершина
конуса лежит на
сфере, а основание
конуса является
сечением сферы
а)
б)

12.

учитель Можарова Е.Н.
ВЫХОД