Похожие презентации:
Неравенства в геометрии
1.
Двадцать первое декабряКлассная работа
Неравенства в геометрии
2.
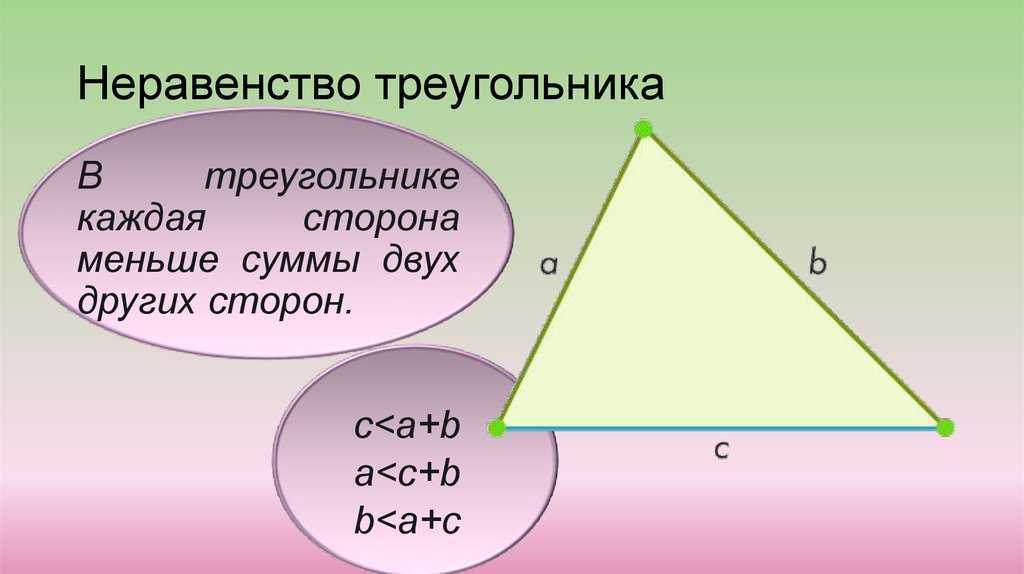
Неравенство треугольникаВ
треугольнике
каждая
сторона
меньше суммы двух
других сторон.
c<a+b
a<c+b
b<a+c
3.
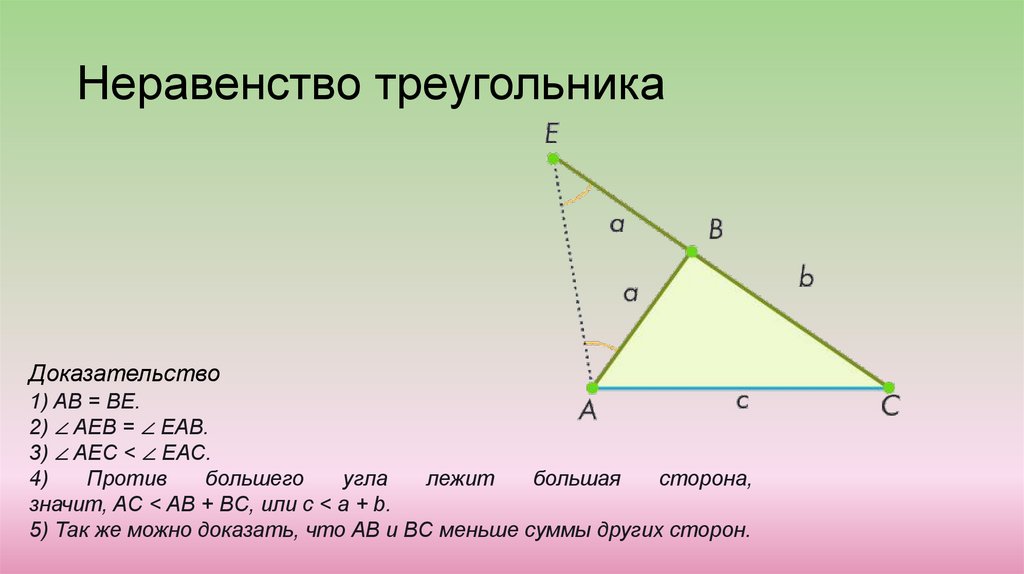
Неравенство треугольникаДоказательство
1) AB = BE.
2) ∠ AEB = ∠ EAB.
3) ∠ AEC < ∠ EAC.
4)
Против
большего
угла
лежит
большая
сторона,
значит, AC < AB + BC, или c < a + b.
5) Так же можно доказать, что AB и BC меньше суммы других сторон.
4.
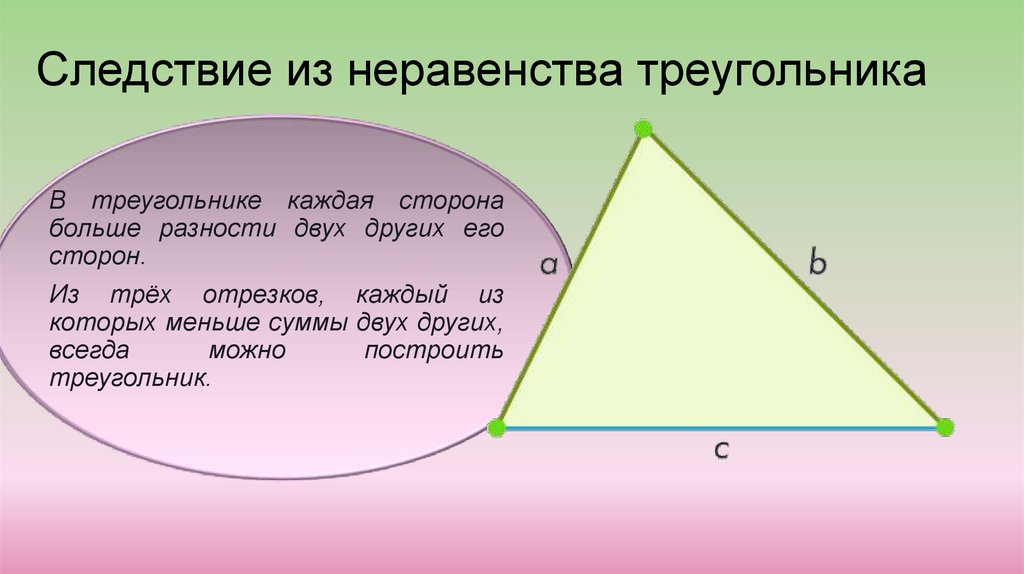
Следствие из неравенства треугольникаВ треугольнике каждая сторона
больше разности двух других его
сторон.
Из трёх отрезков, каждый из
которых меньше суммы двух других,
всегда
можно
построить
треугольник.
5.
1) Постройте треугольник, состоронами равными
5см, 7см и 3см
2) постройте треугольник, со
сторонами равными
5 см,3 см и 1 см – такой
треугольник не существует,
т.к.5 см> 3 см+ 1см
6.
5< 7+37<5+3
3 < 7+5
1 < 5+3
3 < 5+1
5 >1+3
7.
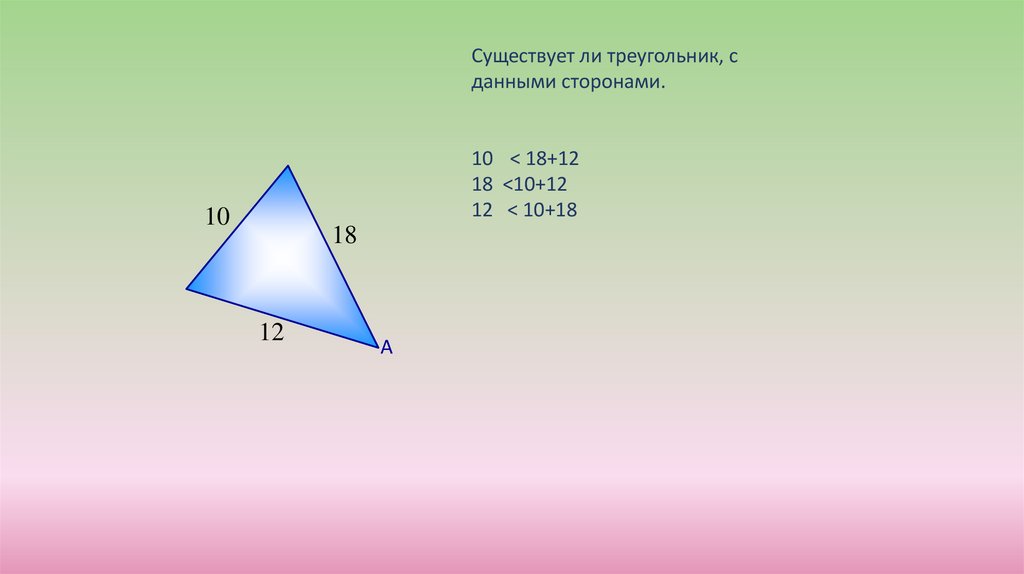
Существует ли треугольник, сданными сторонами.
10 < 18+12
18 <10+12
12 < 10+18
10
18
12
А
8.
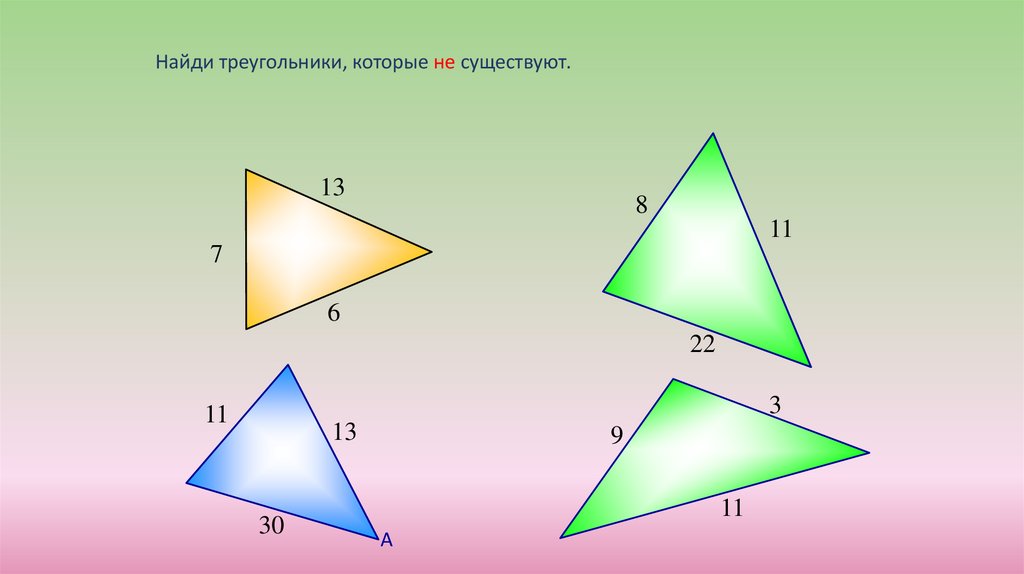
Найди треугольники, которые не существуют.13
8
11
7
6
22
3
11
13
30
9
11
А
9.
Выполним задание10.
Выполним задание11.
Выполним задание12.
Домашнее заданиеп. 34(знать формулировку
теоремы), №№248,250(б)

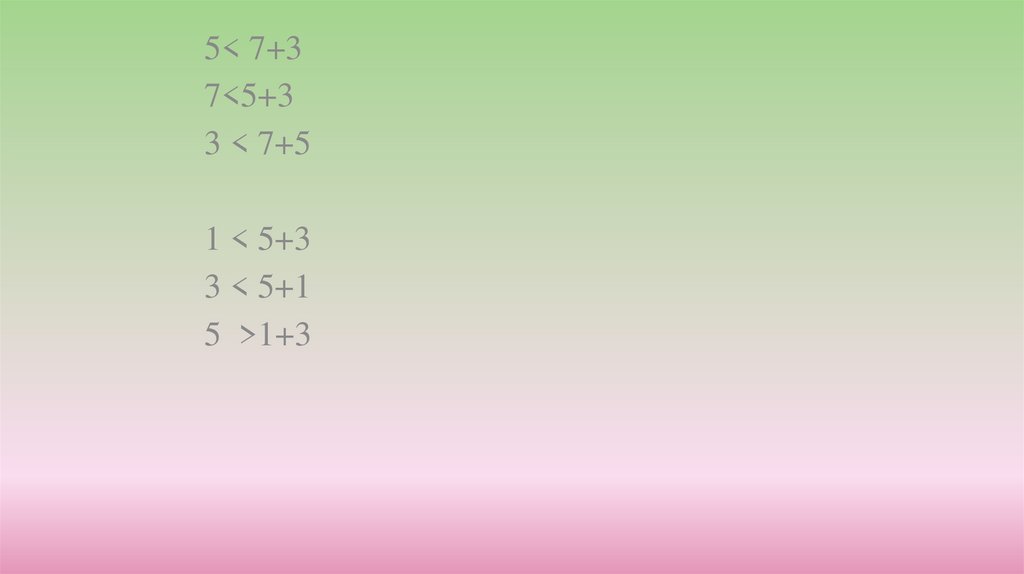




 Математика
Математика








