Похожие презентации:
Призма. Площадь. Поверхности призмы
1.
Геометрия 10 классПРИЗМА.
ПЛОЩАДЬ ПОВЕРХНОСТИ
ПРИЗМЫ
Цели: рассмотреть виды призм, ввести
понятие площади поверхности призмы;
вывести формулу для вычисления площади
поверхности прямой призмы.
2.
I. Проверка домашнего задания(№№ 219, 223)
3.
4.
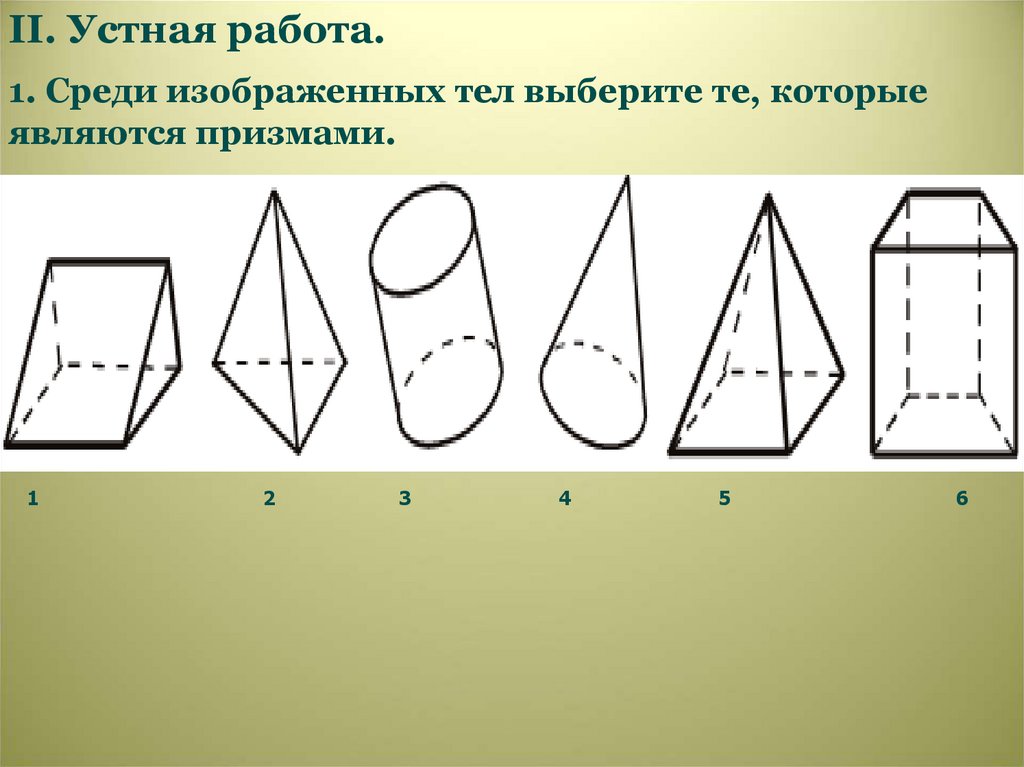
II. Устная работа.1. Среди изображенных тел выберите те, которые
являются призмами.
1
2
3
4
5
6
5.
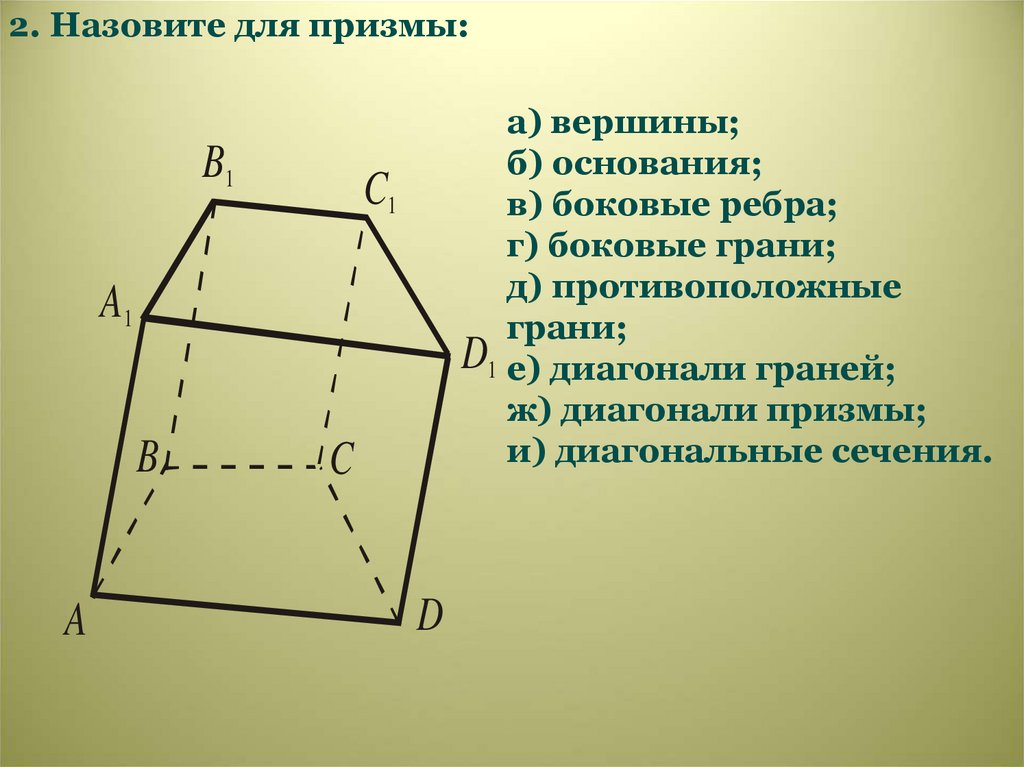
2. Назовите для призмы:B1
а) вершины;
б) основания;
в) боковые ребра;
г) боковые грани;
д) противоположные
грани;
D1 е) диагонали граней;
ж) диагонали призмы;
и) диагональные сечения.
C1
A1
B
A
C
D
6.
3. Закончите предложения.1) Высотой призмы называется…
2) Диагональю призмы называется…
3) Диагональным сечением призмы называется сечение плоскостью,
проходящей через…
4) Параллелепипедом называется…
5) Прямоугольным параллелепипедом называется…
6) Кубом называется прямоугольный параллелепипед, у которого…
7) Примеры моделей призмы и параллелепипеда из реальной жизни:..
4. Ответьте на вопросы:
1) Какие многоугольники лежат в основании призмы?
2) В каких плоскостях лежат основания призмы?
3) Какими отрезками являются боковые ребра призмы?
4) Какими фигурами являются боковые грани призмы?
5) Что представляет собой диагональное сечение призмы?
6) Какими фигурами являются все грани параллелепипеда?
7) Какими фигурами являются все грани прямоугольного
параллелепипеда?
8) Сколько измерений у прямоугольного параллелепипеда?
9) Почему все высоты призмы равны между собой?
10) Какие многоугольники являются основанием и боковой гранью
пятиугольной призмы?
11) Призма имеет 30 граней. Какой многоугольник лежит в ее
основании? Сколько вершин и ребер имеет эта призма?
12) Сколько диагоналей можно провести в четырехугольной призме?
7.
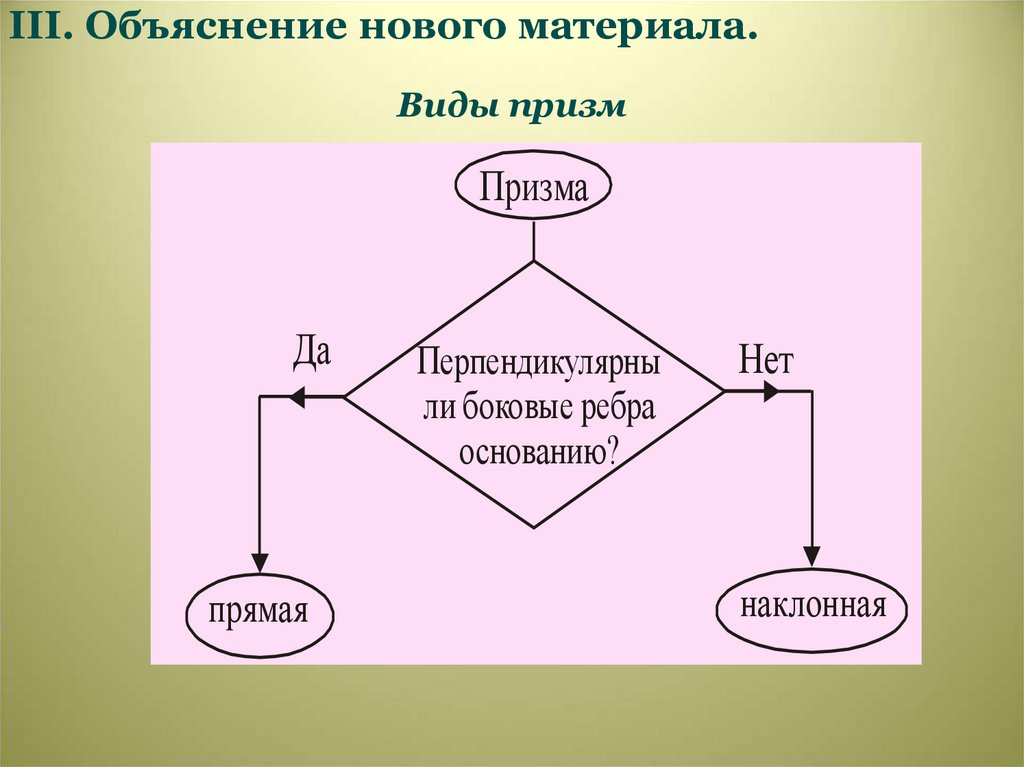
III. Объяснение нового материала.Виды призм
Призма
Да
прямая
Перпендикулярны
ли боковые ребра
основанию?
Нет
наклонная
8.
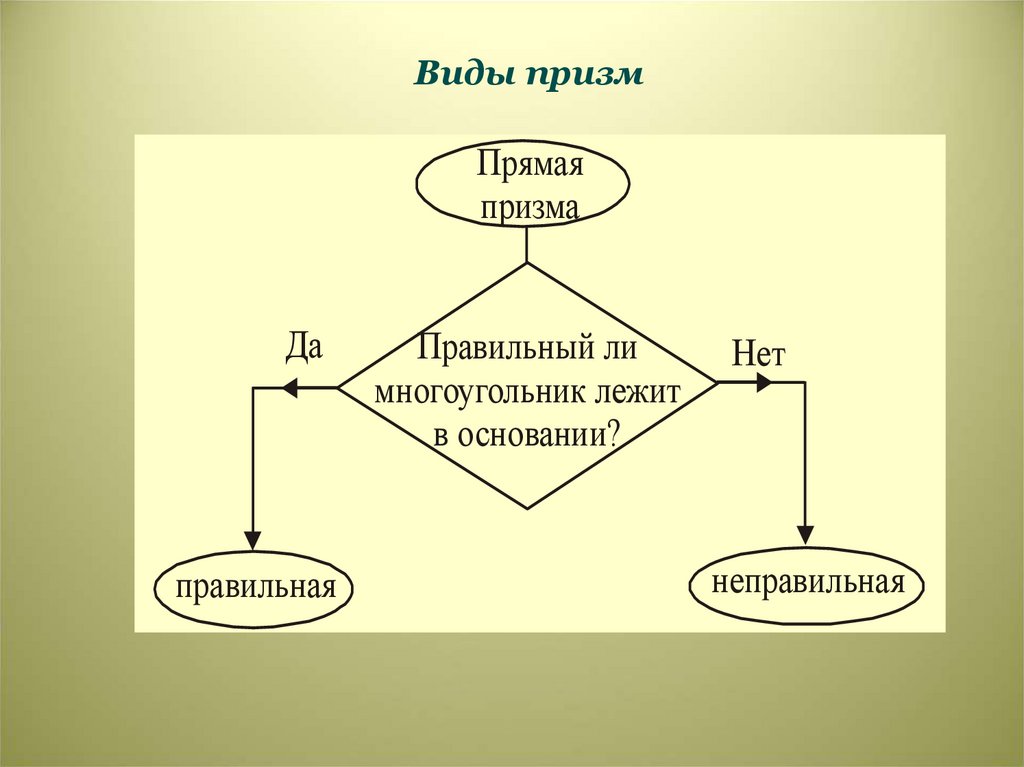
Виды призмПрямая
призма
Да
правильная
Правильный ли
многоугольник лежит
в основании?
Нет
неправильная
9. Прямые призмы
Устно № 218.10. Наклонные призмы
Далее ввести понятие боковой поверхности,полной поверхности прямой призмы (п. 30).
Можно использовать развертки призм.
11. Устно № 218.
IV. Решение задач: №№ 221,222, 225, 230.
Домашнее
задание: теория
(п. 30), №№ 224, 229, 231.







 Математика
Математика








