Похожие презентации:
Математический анализ. 1 курс, 1-й семестр
1.
Математическийанализ
1 курс, 1-й семестр
2.
1. Множества, числовыемножества
2
3.
Лекция 1Множества
4.
Лекция 1Множества
5.
Лекция 1Операции с множествами
6.
Лекция 1Операции внутри множества
Если операция на множестве является бинарной, то говорим, что
множество замкнуто относительно данной операции.
Например, множество натуральных чисел не является замкнутым
относительно операции «деление».
7.
Числовые множестваЛекция 1
8.
Сравнение множеств. МощностьКаких чисел больше – натуральных или целых?
А как сравнивать бесконечные множества?
Лекция 1
9.
Сравнение множеств. МощностьДва множества называются равномощными (имеют одинаковую
мощность), если между их элементами существует взаимнооднозначное соответствие, т.е. каждому элементу одного множества
можно поставить в соответствие ровно один элемент другого и
наоборот.
Лекция 1
10.
Сравнение множеств. МощностьКаких чисел больше – натуральных или рациональных?
Следствие.
Между любыми двумя различными рациональными числами
существует бесконечно много других рациональных.
Лекция 1
11.
Сравнение множеств. МощностьЛекция 1
Каких чисел больше – натуральных или рациональных?
Множества, равномощные множеству натуральных чисел, называются
счетными. Конечные и счетные множества образуют класс не более,
чем счетных множеств.
12.
Сравнение множеств. МощностьЛекция 1
13.
Отображения на множествахЛекция 1
14.
Отображения на множествахЛекция 1
15.
Теорема КантораЛекция 1
16.
Аксиоматика множества действительных чиселМы будем использовать аксиоматический метод построения
множества действительных чисел, в котором оно определяется как
множество элементов с операциями сложения, умножения и
отношением порядка.
Свойства операций и отношения порядка и взамимосвязь между
ними задаются системой аксиом, разбитой на четыре группы.
В первую группу входят аксиомы сложения,
во вторую — аксиомы умножения,
в третью — аксиомы порядка,
в четвертую — аксиома о верхней грани.
Итак:
Лекция 2
17.
Аксиоматика множества действительных чиселЛекция 2
18.
Аксиоматика множества действительных чиселЛекция 2
19.
Лекция 2Аксиоматика множества действительных чисел
20.
Лекция 2Аксиоматика множества действительных чисел
4.1. Аксиома о верхней грани:
Всякое ограниченное сверху множество обладает точной верхней гранью.
21.
Лекция 3Аксиоматика множества действительных чисел
Про рациональные числа уже все известно. А что такое все-таки
иррациональное число?
Именно аксиома о существовании верхней грани позволяет дать
определение иррационального числа.
Точная верхняя грань ограниченного сверху множества рациональных
чисел, не являющаяся рациональным числом, называется
иррациональным числом.
22.
Лекция 3Аксиоматика множества действительных чисел
По жизни и для целей программирования достаточным и привычным
является следующее представление действительных чисел.
Рациональное число – число, представимое в виде периодической
десятичной дроби;
Иррациональное число – число, представимое в виде непериодической
десятичной дроби.
23.
Лекция 3Комплексные числа
24.
Лекция 3Комплексные числа
25.
Лекция 3Принцип математической индукции
26.
Лекция 3Принцип математической индукции
27.
2. Предел числовойпоследовательтности
27
28.
Лекция 4Числовая последовательность
Примеры.
или
или
29.
Лекция 4Числовая последовательность
30.
Лекция 4Числовая последовательность
Примеры.
или
или
31.
Лекция 4Определение предела последовательности
32.
Лекция 4Определение предела последовательности
33.
Лекция 4Некоторые теоремы о пределах
Лемма 1 (единственность предела).
Если последовательность имеет предел, то он единственен.
34.
Лемма 7.Некоторые теоремы о пределах
Лемма 5.
Лемма 6.
Лекция 4
35.
Лекция 4Некоторые теоремы о пределах
Лемма 7.
36.
Лекция 4Неопределенности
1.
37.
Лекция 4Неопределенности
2.
38.
Лекция 4Неопределенности
3.
39.
Лекция 4Неопределенности
4.
40.
Лекция 4Монотонные последовательности
- возрастающая последовательность
- неубывающая последовательность
- убывающая последовательность
- невозрастающая последовательность
41.
Лекция 4Монотонные последовательности
Примеры
42.
Лекция 4Последовательность возрастающая.
43.
Лекция 4Последовательность ограничена сверху.
Возрастает и ограничена сверху, следовательно, имеет
конечный предел.
44.
Лекция 4Подпоследовательности. Лемма Больцано-Вейерштрасса
Лемма (Больцано, Вейерштрасс)
Из любой ограниченной последовательности можно выделить
сходящуюся подпоследовательность.
45.
Лекция 4Фундаментальные последовательности. Критерий Коши
Теорема (Коши)
Для того чтобы последовательность имела конечный предел,
необходимо и достаточно, чтобы она была фундаментальной.
46.
Лекция 4Верхний и нижний пределы последовательности
47.
3. Числовые функции47
48.
Понятие функции. Способы задания49.
Понятие функции. Способы заданияАналитический способ.
Табличный способ.
Графический способ.
50.
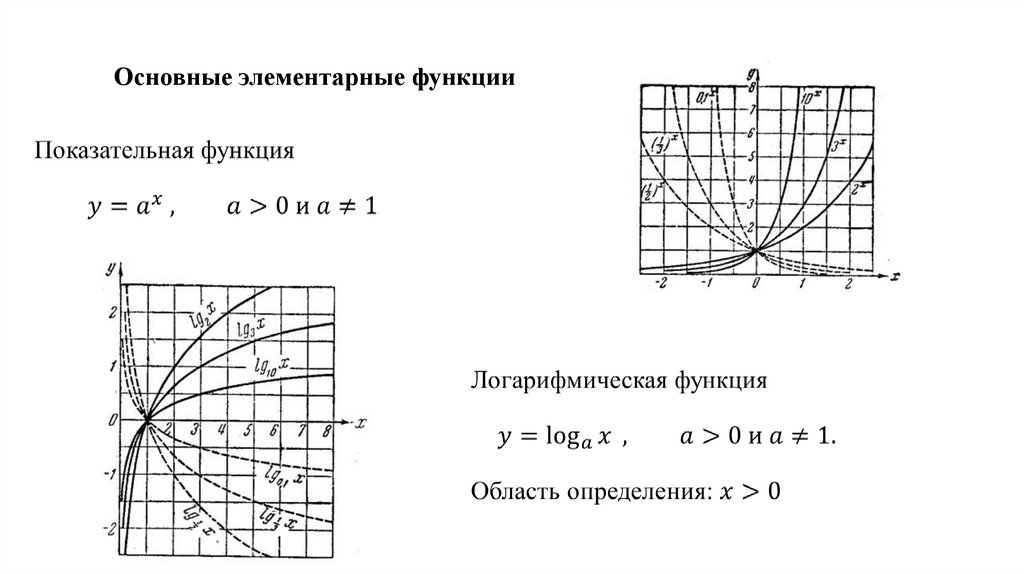
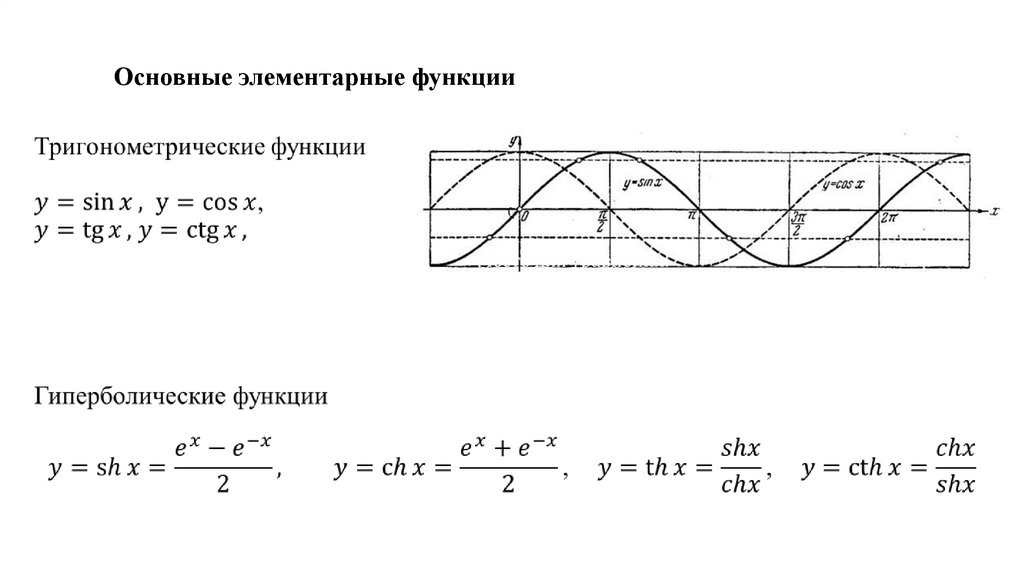
Основные элементарные функции51.
Основные элементарные функции52.
Основные элементарные функции53.
Основные элементарные функции54.
Основные элементарные функции55.
Суперпозиция функция (сложная функция)56.
Обратная функцияПримеры
57.
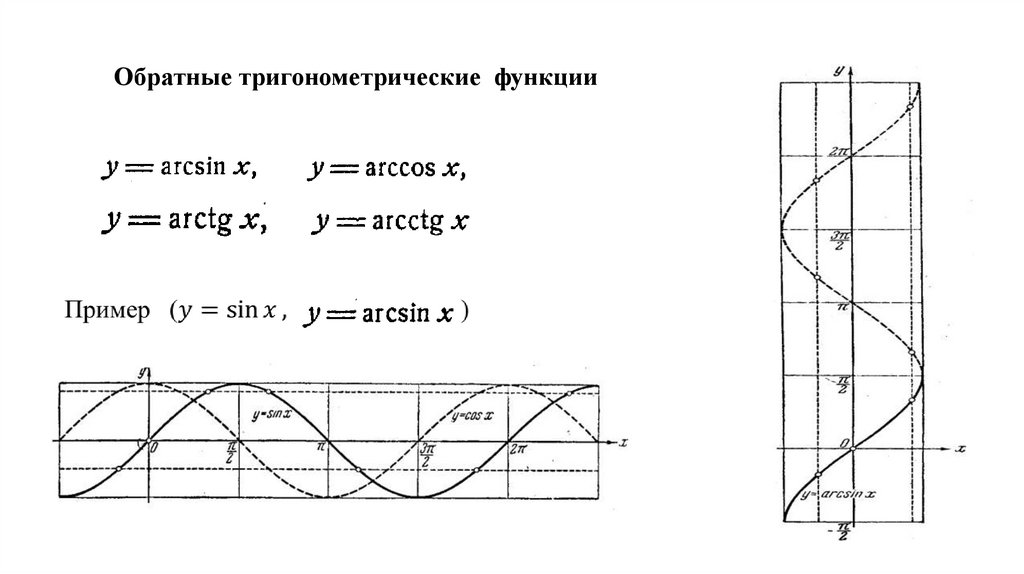
Обратные тригонометрические функции58.
4. Предел функции58
59.
Предел функции; слева:
Легко показать, что
тогда и только тогда, когда
60.
Предел функции, как предел числовой последовательности61.
Предел функции, как предел числовой последовательности62.
Теоремы о пределе функции63.
Неопределенности-- первый
замечательный
предел
-- второй замечательный предел
64.
Критерий существования предела функции65.
Сравнение бесконечно малых величин66.
Сравнение бесконечно больших величин67.
5. Непрерывностьфункции
67
68.
Непрерывность функции в точкеЕсли это соотношение не выполняется, то говорим, что при этом
значении (или в этой точке) функция имеет разрыв.
69.
Непрерывность функции в точке70.
Непрерывность функции на промежутке71.
Непрерывность элементарных функции72.
Непрерывность элементарных функциит.к. модуль косинуса всегда меньше единицы, модуль синуса меньше модуля
его аргумента, если он (аргумент) достаточно мал.
73.
Непрерывность элементарных функцииИз непрерывности синуса и косинуса по последней теореме вытекают
непрерывность тангенса и котангенса.
Также существуют доказательства непрерыности остальных элементарных
функций: логарифмическая, степенная, обратные тригонометрические.
(Доказательства опускаем.)






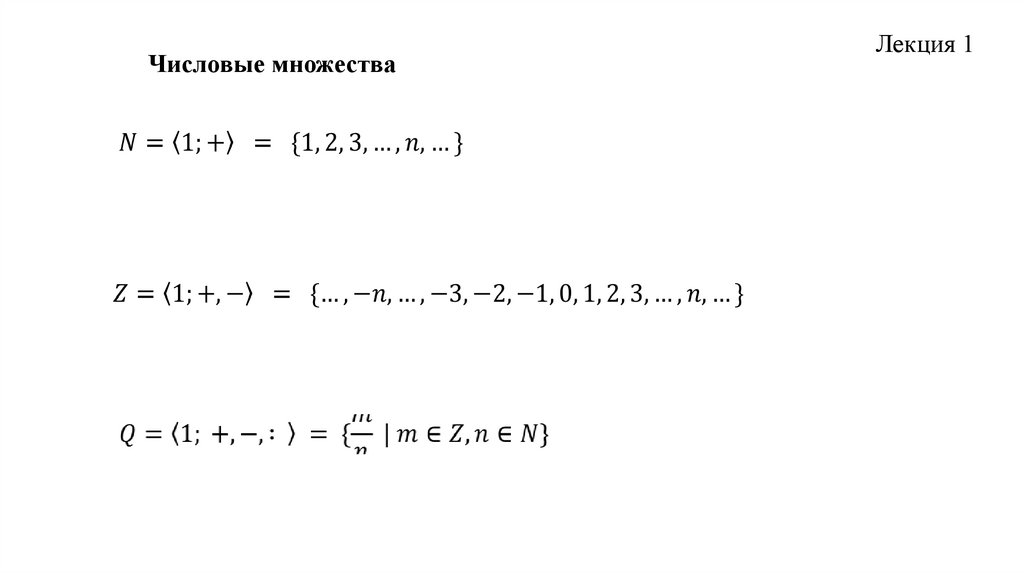


































































 Математика
Математика








