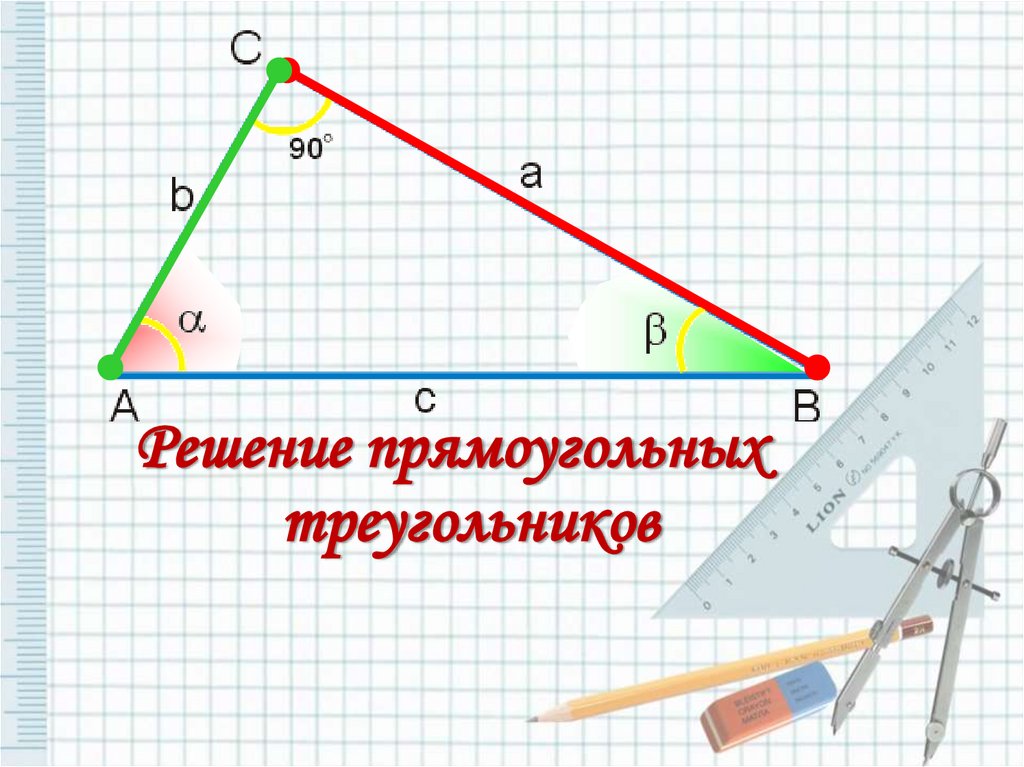
Решение прямоугольных треугольников

1.

Решение прямоугольных
треугольников

2.

СI

3.

№1
Дано: РКМ, К = 900
РК = 1 см, РМ = 2 см.
Найти: Р, М, КМ.
КМ 3
Какие элементы прямоугольного
треугольника были известны?
М 30
Гипотенуза и катет
Р 60
0
0
Какие еще элементы треугольника
мы нашли?
Второй катет и острые углы

4.

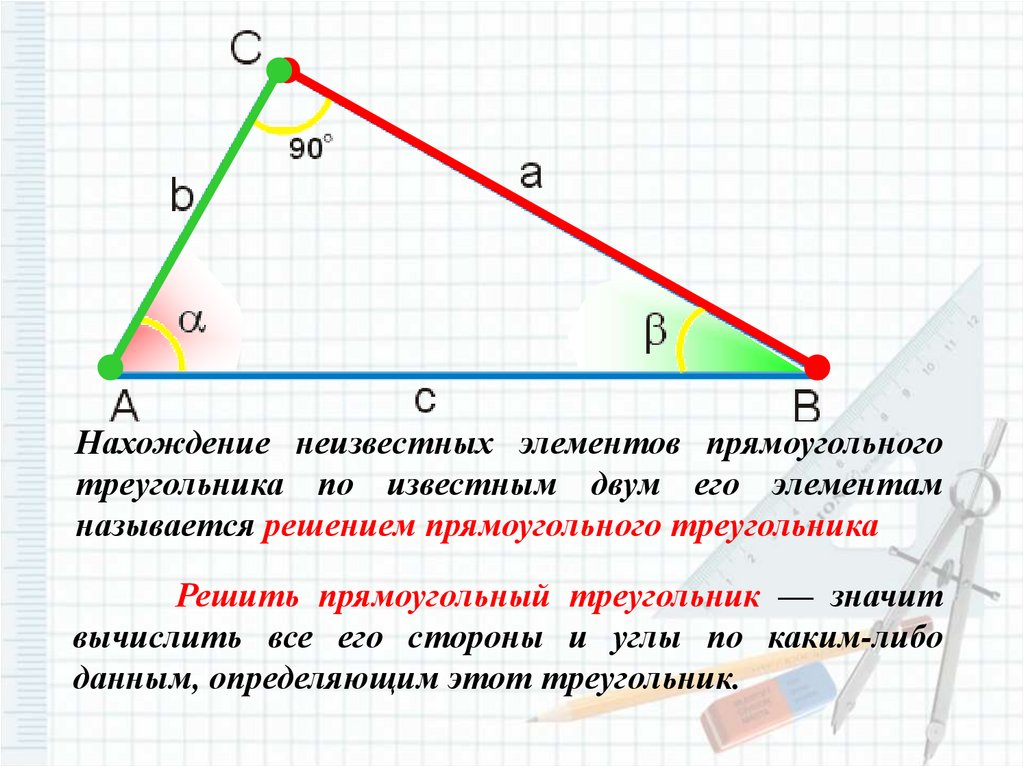
Нахождение неизвестных элементов прямоугольного
треугольника по известным двум его элементам
называется решением прямоугольного треугольника
Решить прямоугольный треугольник — значит
вычислить все его стороны и углы по каким-либо
данным, определяющим этот треугольник.

5.

a
sin
c
B
a c sin
β
c
a c cos
a
α
C
a
cos
c
b
A
a
c
sin
a
c
cos
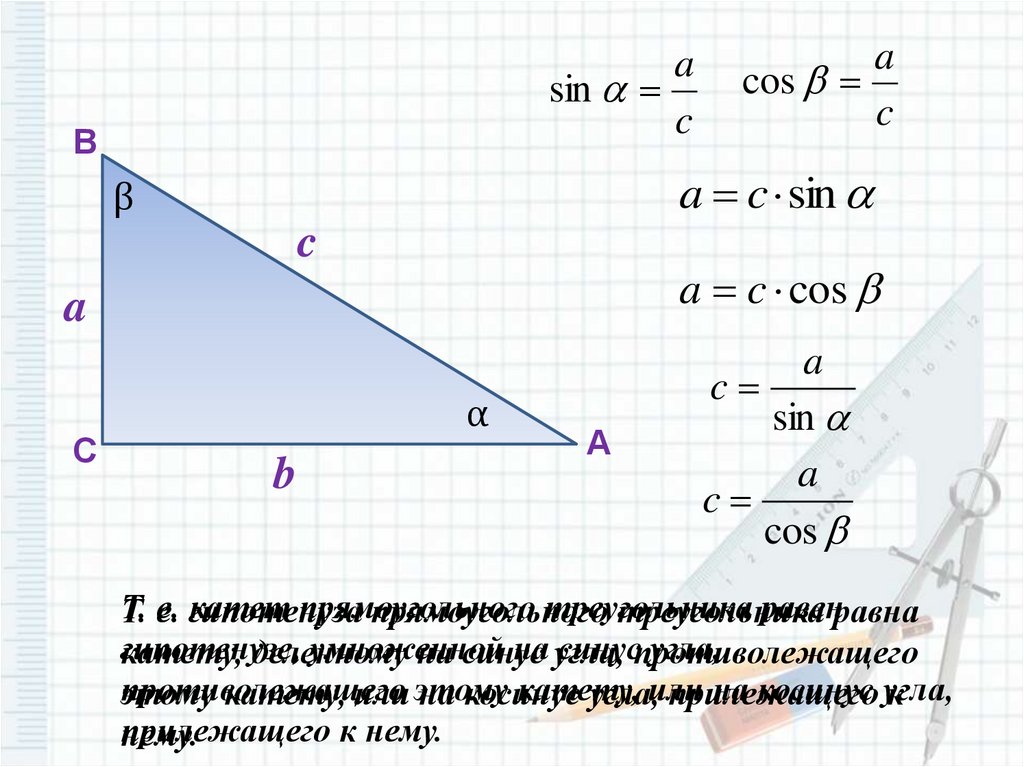
Т. е. гипотенуза
катет прямоугольного
треугольника
равенравна
прямоугольного
треугольника
гипотенузе,
умноженной
на угла,
синуспротиволежащего
угла,
катету, деленному
на синус
противолежащего
катету,
на косинус угла,
этому
катету, или этому
на косинус
угла,или
прилежащего
к
прилежащего к нему.
нему.

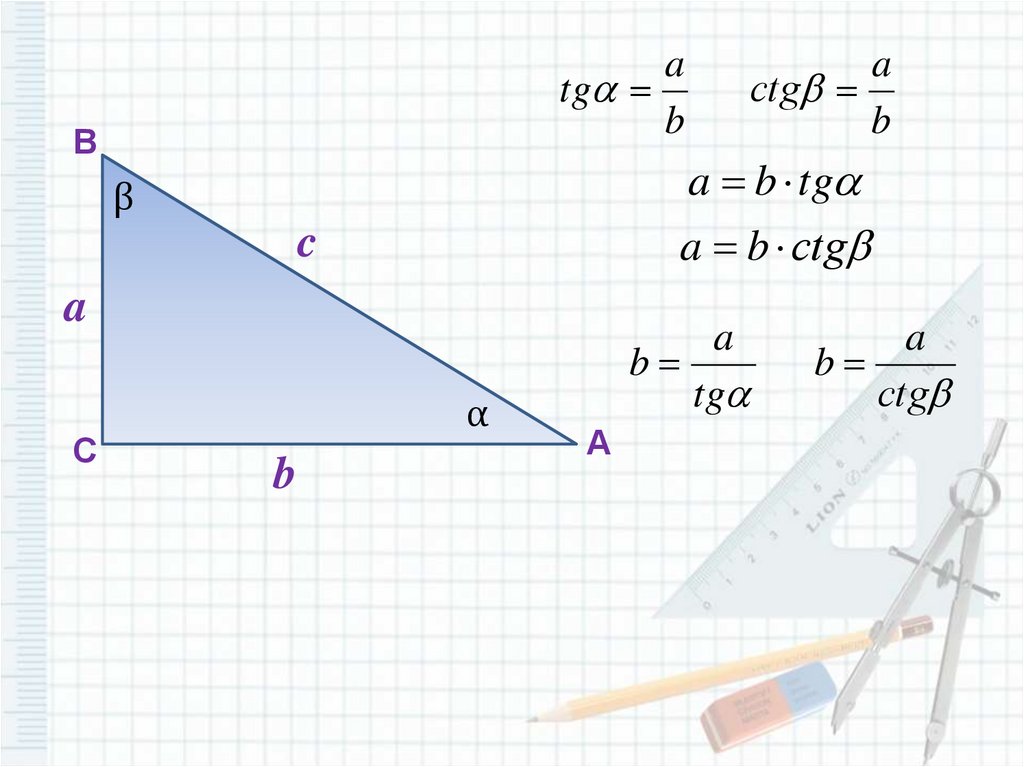
6.

a
tg
b
B
a b tg
a b сtg
β
c
a
α
C
b
a
сtg
b
a
b
tg
A
a
b
сtg

7.

ЗАДАНИЕ:
Опишите возможные случаи задания прямоугольного треугольника по
двум элементам.
B
B
c
a
B
B
c
a
α
α
C
A C
b
b
A C
A C
A
Два катета
Катет и
гипотенуза
Катет и
острый угол
c a2 b2
а c 2 b2
В 900 А В 900 А
a
tgA
b
sin В
В 90 А
0
b
c
А 90 В
0
Гипотенуза и
острый угол
b atgB
a c * sin A
c a2 b2
b c2 a2

8.

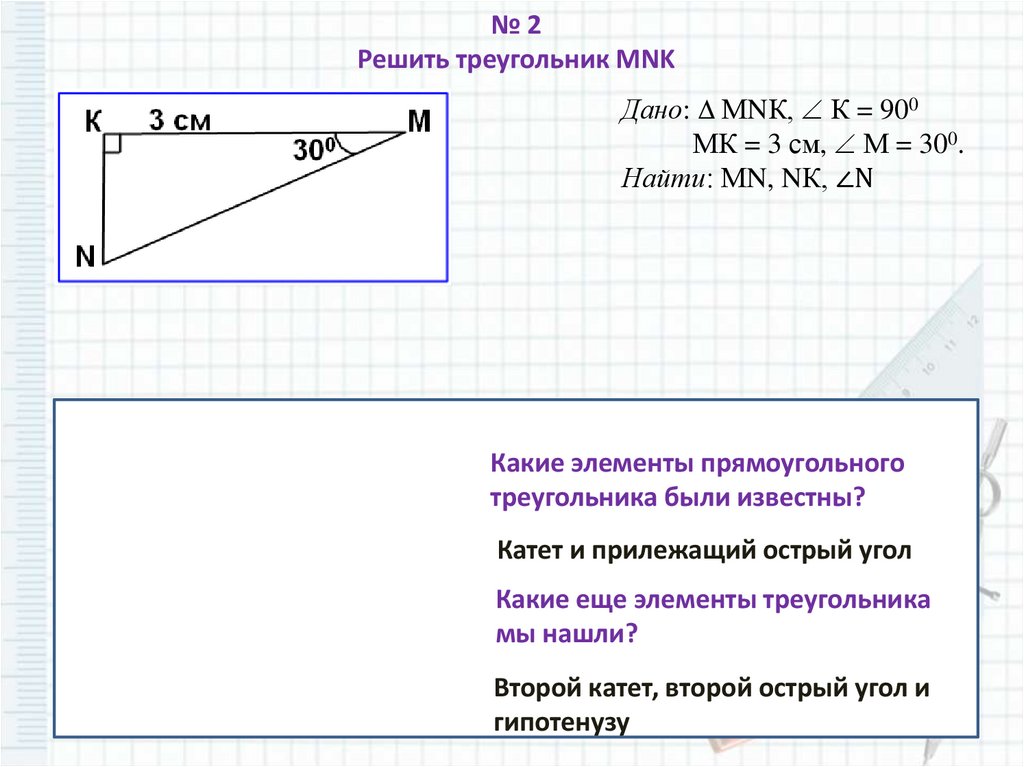
№2
Решить треугольник MNK
Дано: МNК, К = 900
МК = 3 см, М = 300.
Найти: МN, NК, ∠N
Какие элементы прямоугольного
треугольника были известны?
Катет и прилежащий острый угол
Какие еще элементы треугольника
мы нашли?
Второй катет, второй острый угол и
гипотенузу

9.

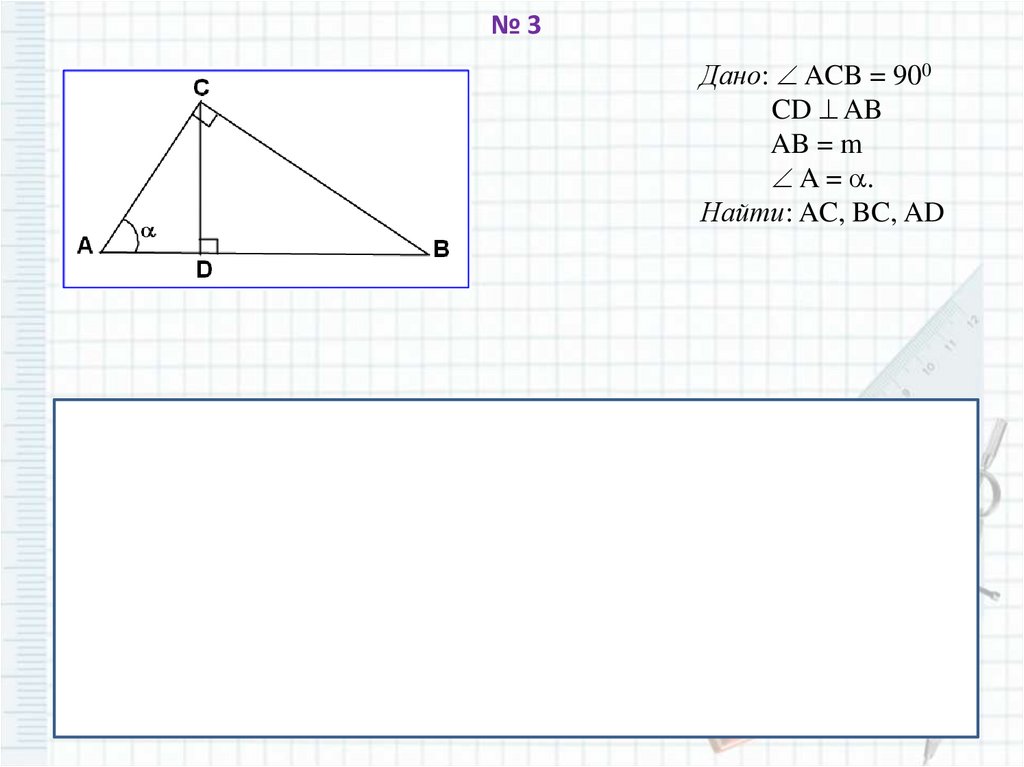
№3
Дано: ACB = 900
CD AB
AB = m
A = .
Найти: AC, BC, AD

10.

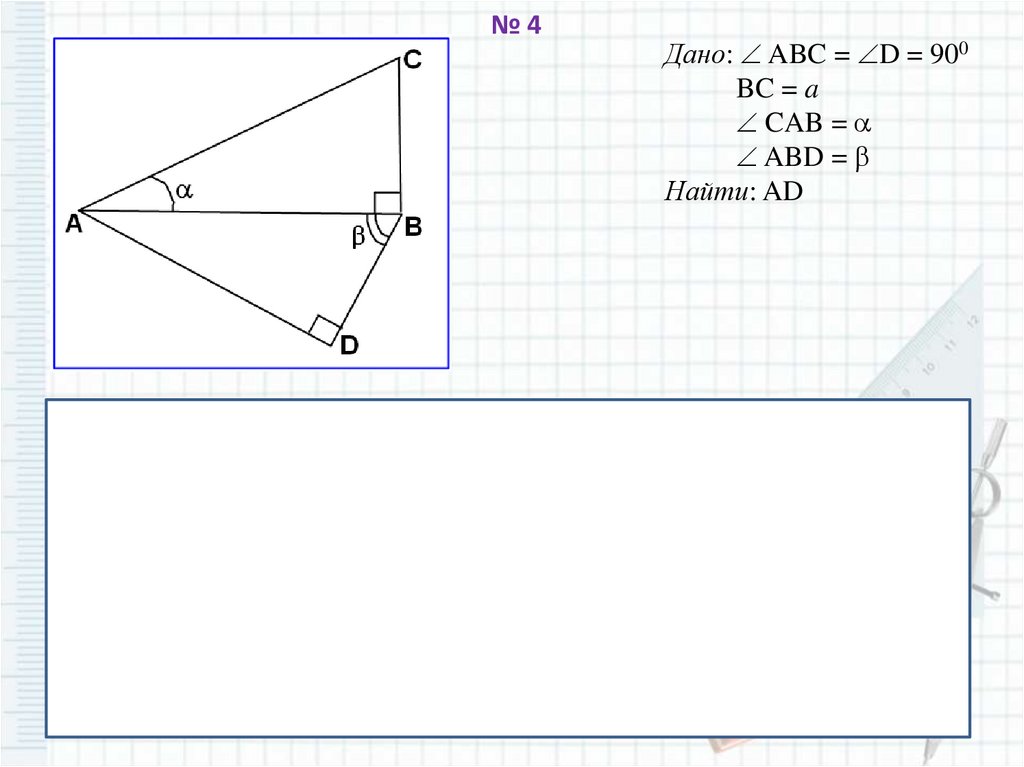
№4
Дано: ABC = D = 900
BC = a
CAB =
ABD =
Найти: AD

11.

На какую высоту
поднялся матрос,
прошедший 10 метров
по трапу,
составлявшему с
пристанью угол 30 ?
10 м
?м
30ᵒ

12.

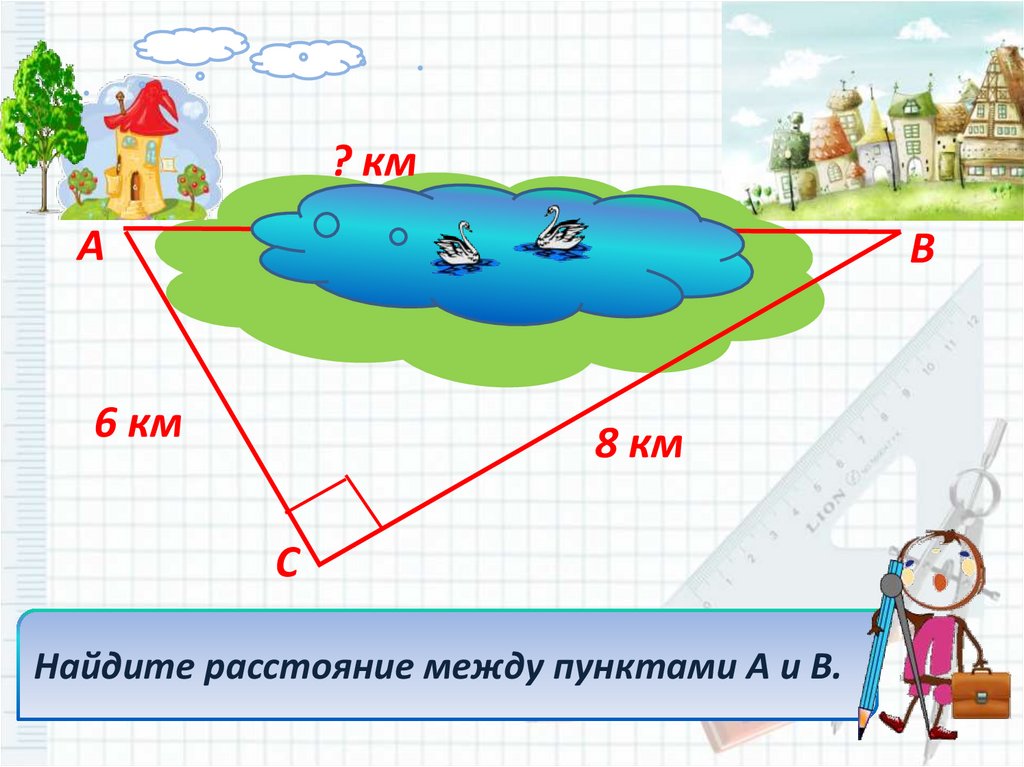
? км
A
B
6 км
8 км
С
Найдите расстояние между пунктами А и В.

13.

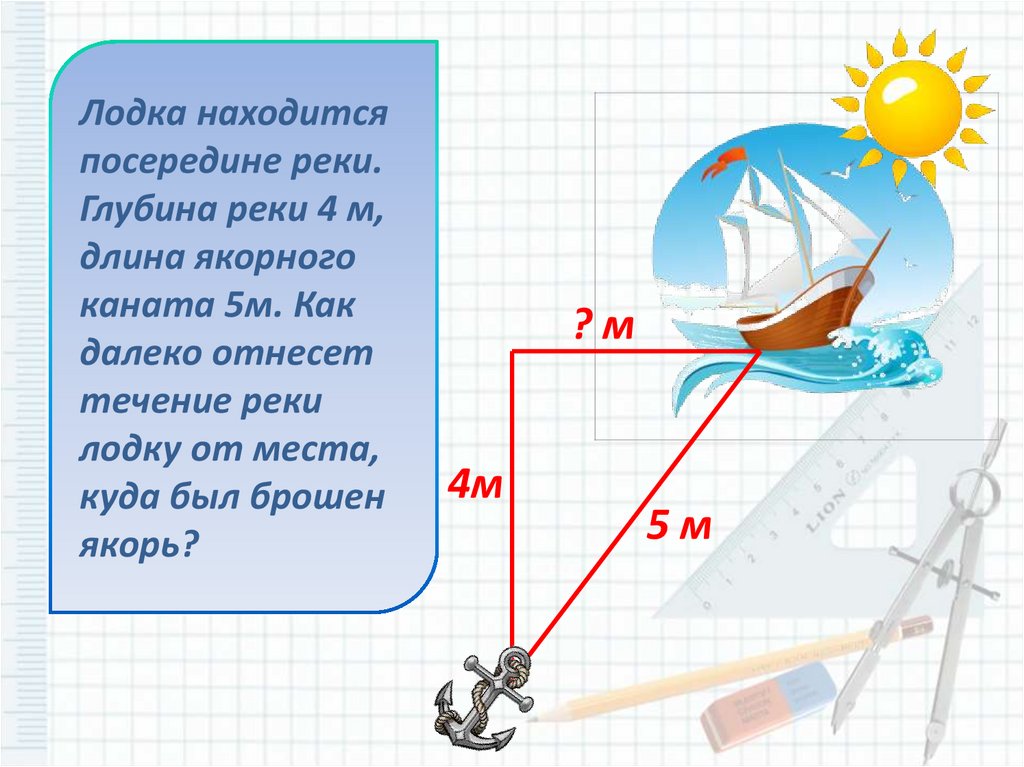
Лодка находится
посередине реки.
Глубина реки 4 м,
длина якорного
каната 5м. Как
далеко отнесет
течение реки
лодку от места,
куда был брошен
якорь?
?м
4м
5м

14.

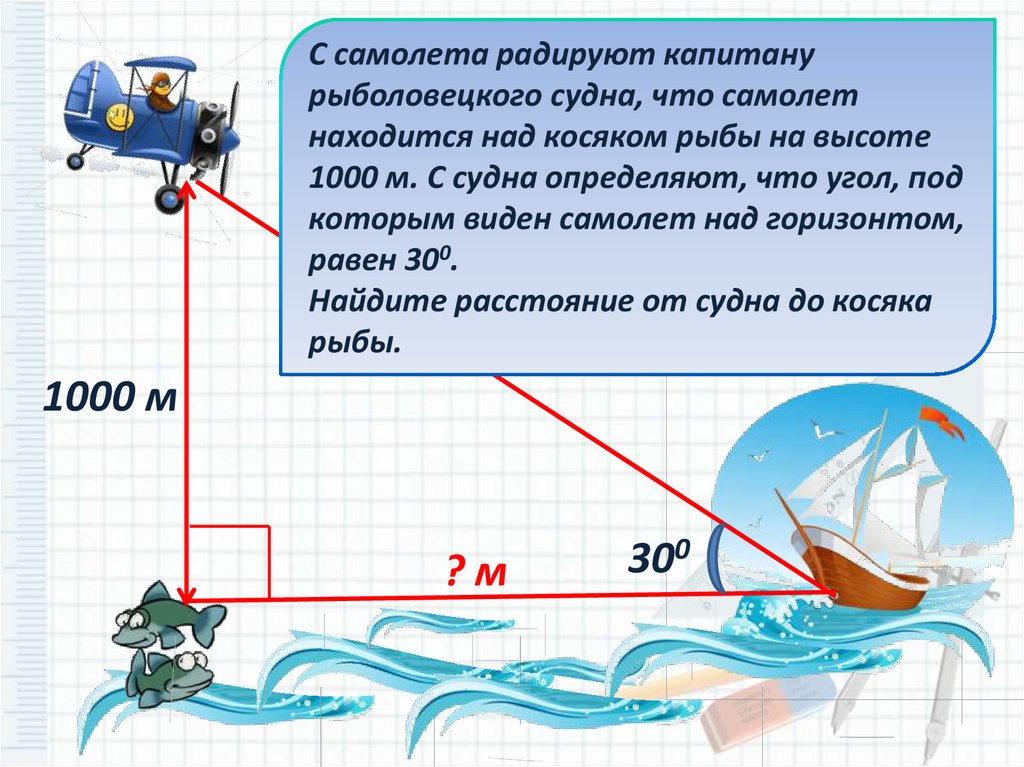
С самолета радируют капитану
рыболовецкого судна, что самолет
находится над косяком рыбы на высоте
1000 м. С судна определяют, что угол, под
которым виден самолет над горизонтом,
равен 300.
Найдите расстояние от судна до косяка
рыбы.
1000 м
?м
300

15.

Мальчик и девочка, расставшись на
перекрестке, пошли по взаимно
перпендикулярным дорогам, мальчик со
скоростью 4 км/ч, а девочка 3 км/ч. Какое
расстояние (в км) будет между ними через 30
мин?
? км

16.

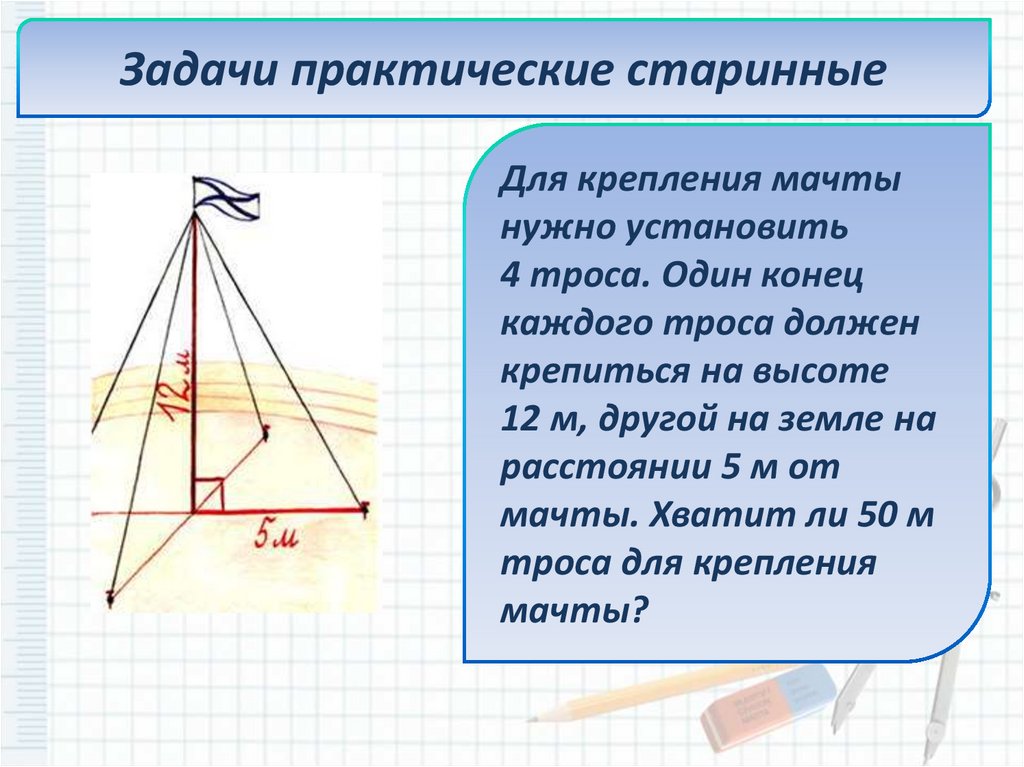
Задачи практические старинные
Для крепления мачты
нужно установить
4 троса. Один конец
каждого троса должен
крепиться на высоте
12 м, другой на земле на
расстоянии 5 м от
мачты. Хватит ли 50 м
троса для крепления
мачты?

17.

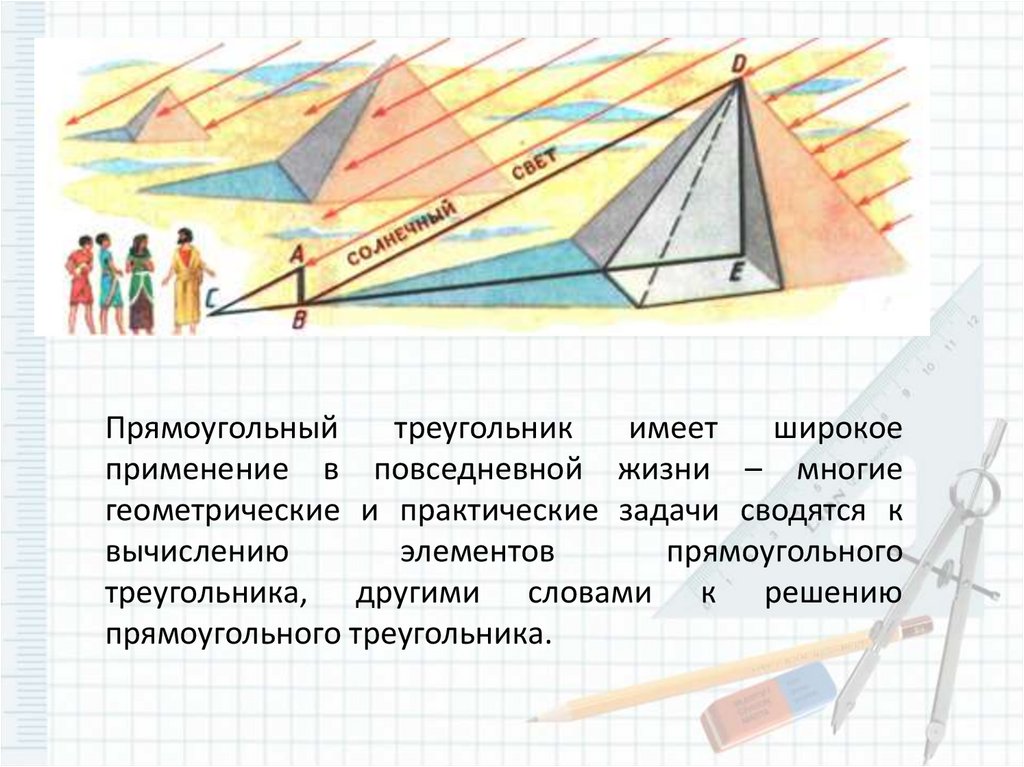
Прямоугольный
треугольник
имеет
широкое
применение в повседневной жизни – многие
геометрические и практические задачи сводятся к
вычислению
элементов
прямоугольного
треугольника, другими словами к решению
прямоугольного треугольника.

18.

Пирамида Кукулькана («оперённый змей»), Юкатан, Мексика

19.

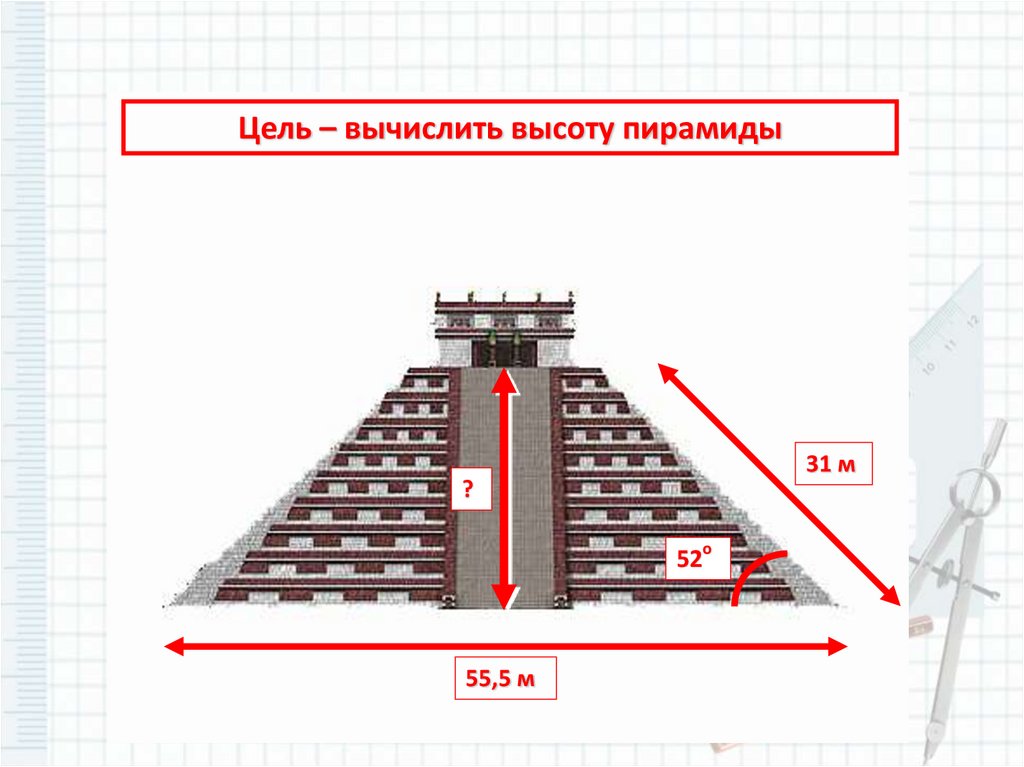
Цель – вычислить высоту пирамиды
31 м
?
52о
55,5 м

20.

А
к
а
т
е
т
?
п
р
о
т
и
в
о
л
е
ж
а
щ
и
й
31 м
гипотенуза
52о
С
к а т е т
В

21.

Гиппарх

22.

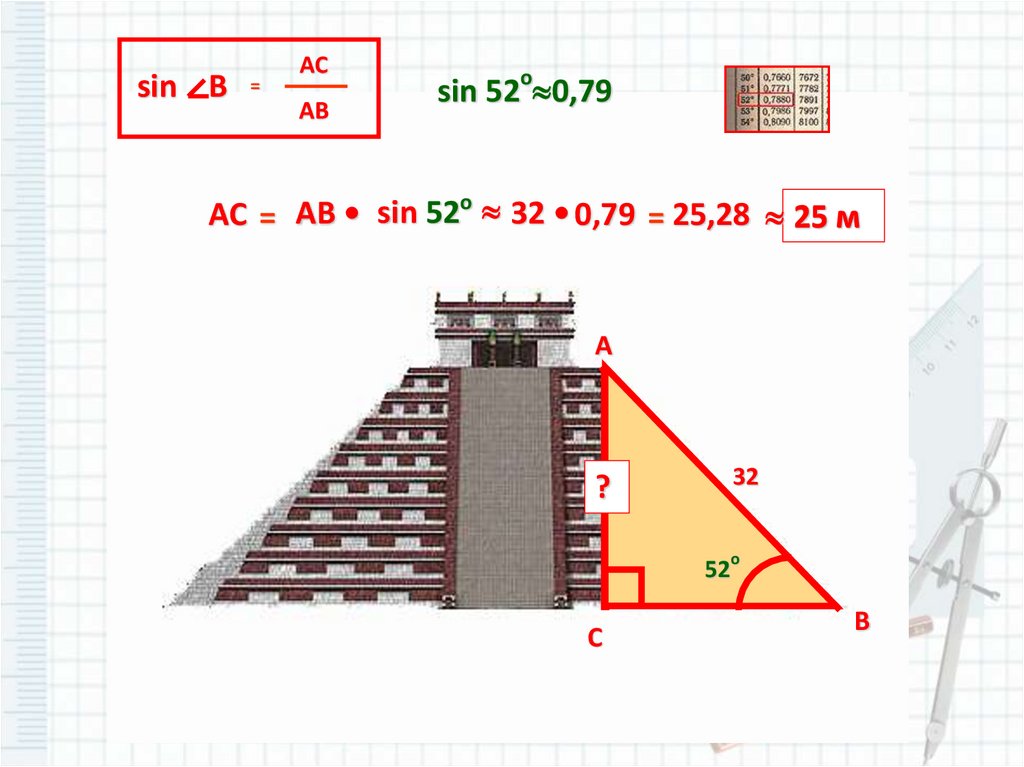
sin В
=
AC
AB
sin 52o 0,79
AC = AB • sin 52o 32 • 0,79 = 25,28 25 м
А
32
?
о
52
С
В

23.

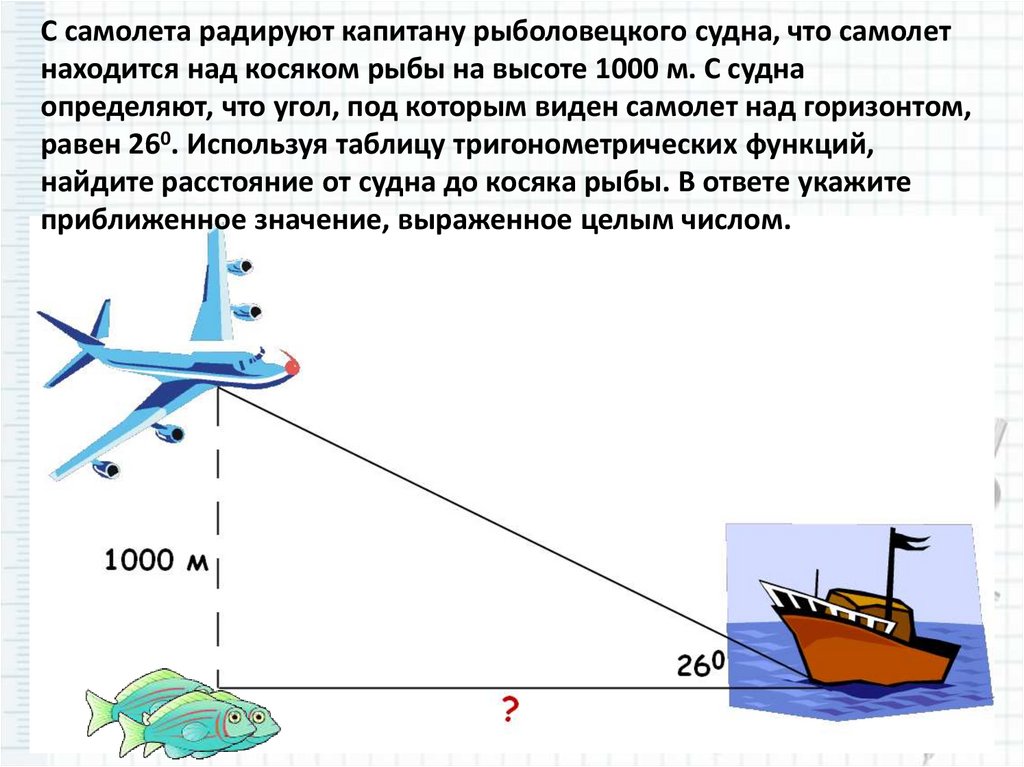
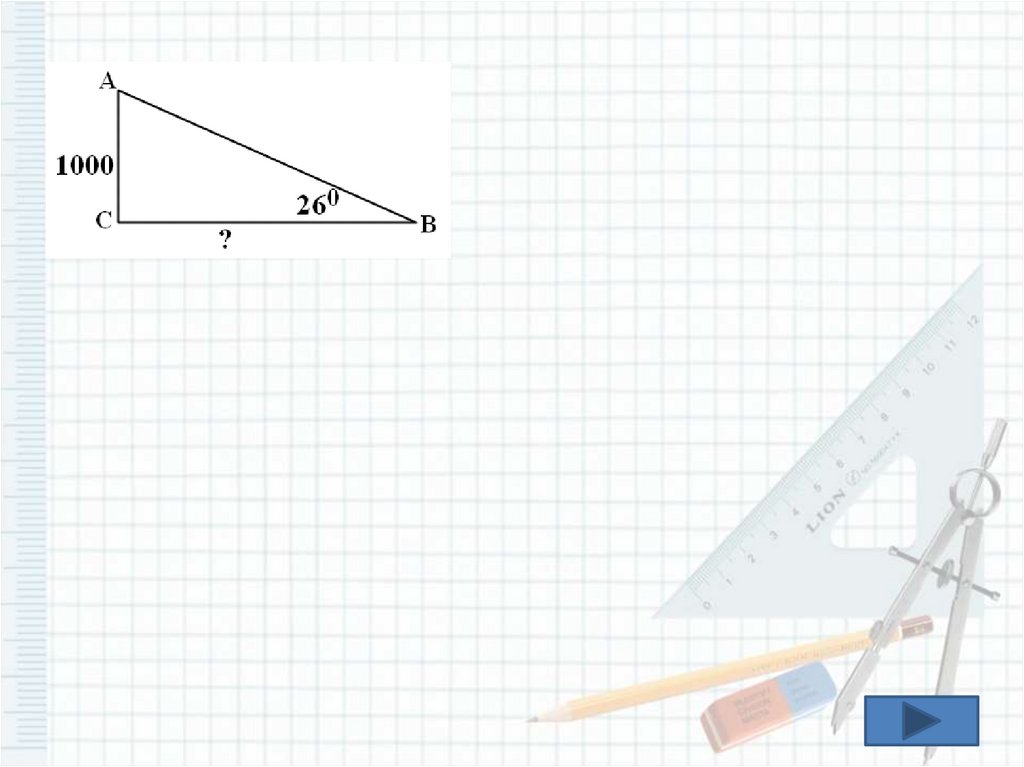
С самолета радируют капитану рыболовецкого судна, что самолет
находится над косяком рыбы на высоте 1000 м. С судна
определяют, что угол, под которым виден самолет над горизонтом,
равен 260. Используя таблицу тригонометрических функций,
найдите расстояние от судна до косяка рыбы. В ответе укажите
приближенное значение, выраженное целым числом.

24.

25.

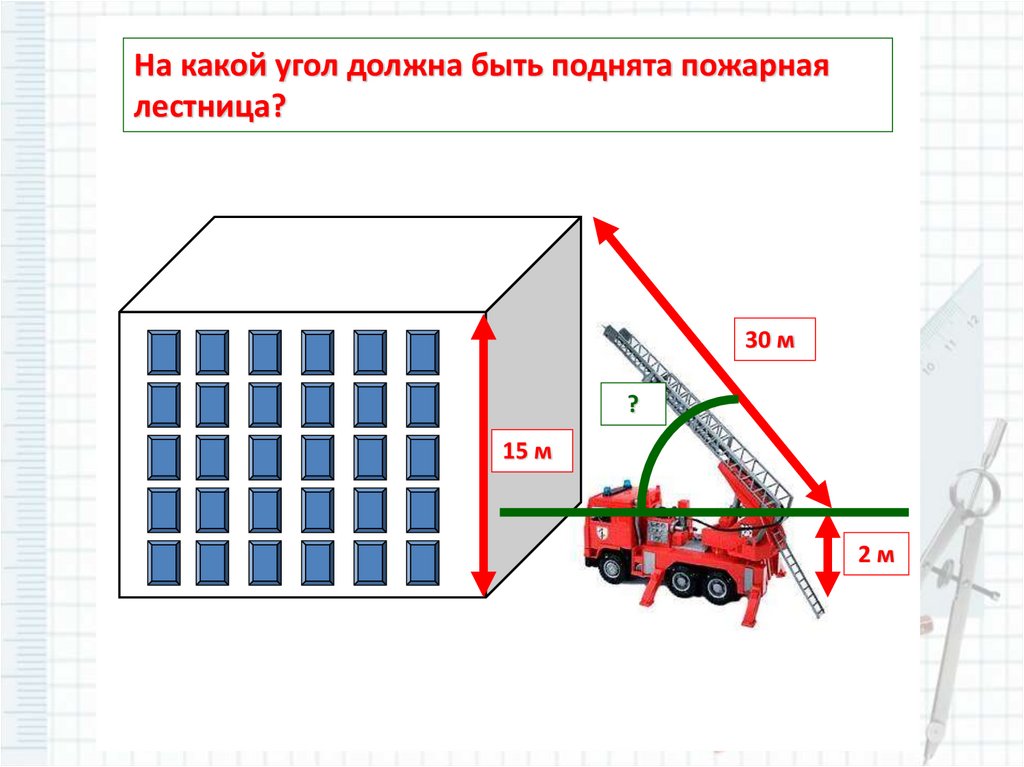
На какой угол должна быть поднята пожарная
лестница?
30 м
?
15 м
2м

26.

Искать
trigonom.i
6
1
pub-2850
ru
GALT:#9A
e7fc-6F8B
0000
windows-1
9137517
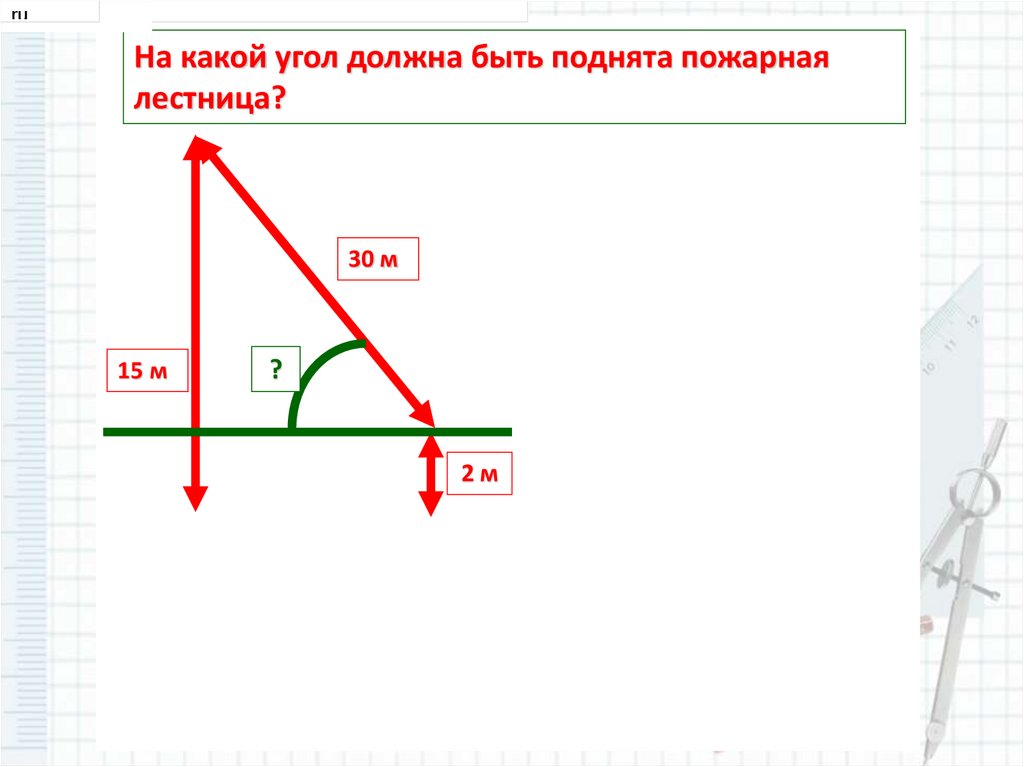
На какой угол должна быть поднята пожарная
лестница?
30 м
15 м
?
2м

27.

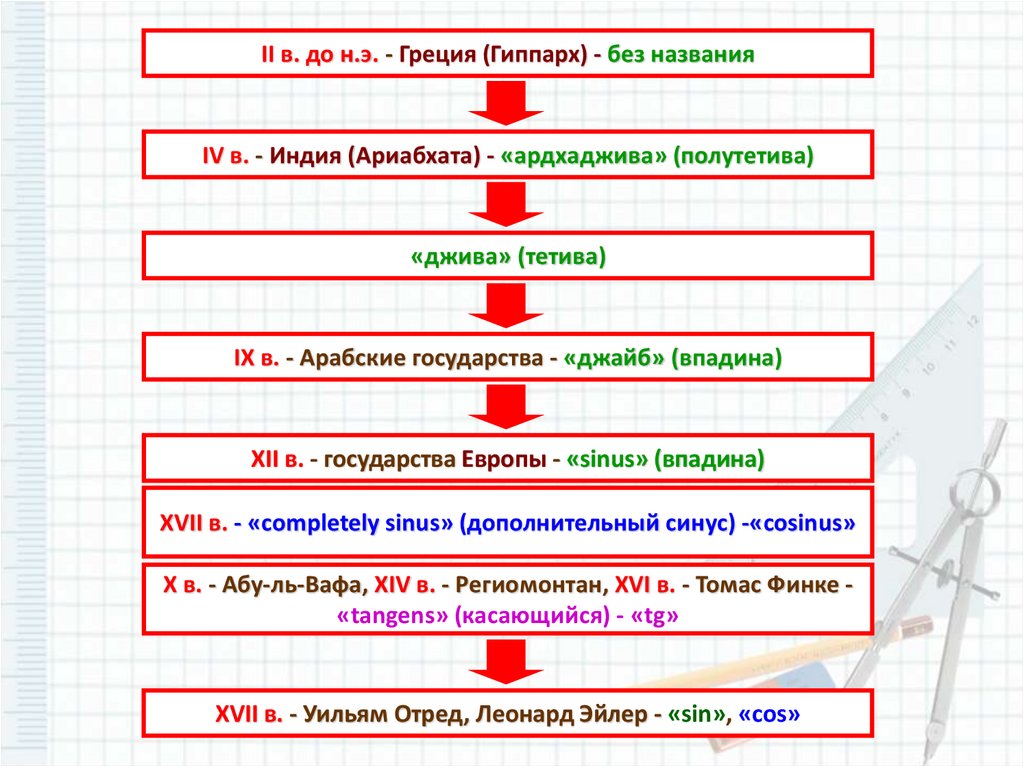
II в. до н.э. - Греция (Гиппарх) - без названия
IV в. - Индия (Ариабхата) - «ардхаджива» (полутетива)
«джива» (тетива)
IX в. - Арабские государства - «джайб» (впадина)
XII в. - государства Европы - «sinus» (впадина)
XVII в. - «completely sinus» (дополнительный синус) -«cosinus»
X в. - Абу-ль-Вафа, XIV в. - Региомонтан, XVI в. - Томас Финке «tangens» (касающийся) - «tg»
XVII в. - Уильям Отред, Леонард Эйлер - «sin», «cos»

28.

1.
2.
3.
4.
5.