Похожие презентации:
Синус, косинус, тангенс острого угла прямоугольного треугольника
1. Синус, косинус, тангенс острого угла прямоугольного треугольника
2.
1.Закончи предложение: «Треугольник, укоторого один угол прямой
называется…»
А) остроугольный
Б) равнобедренный
В) равносторонний
Г) прямоугольный
3.
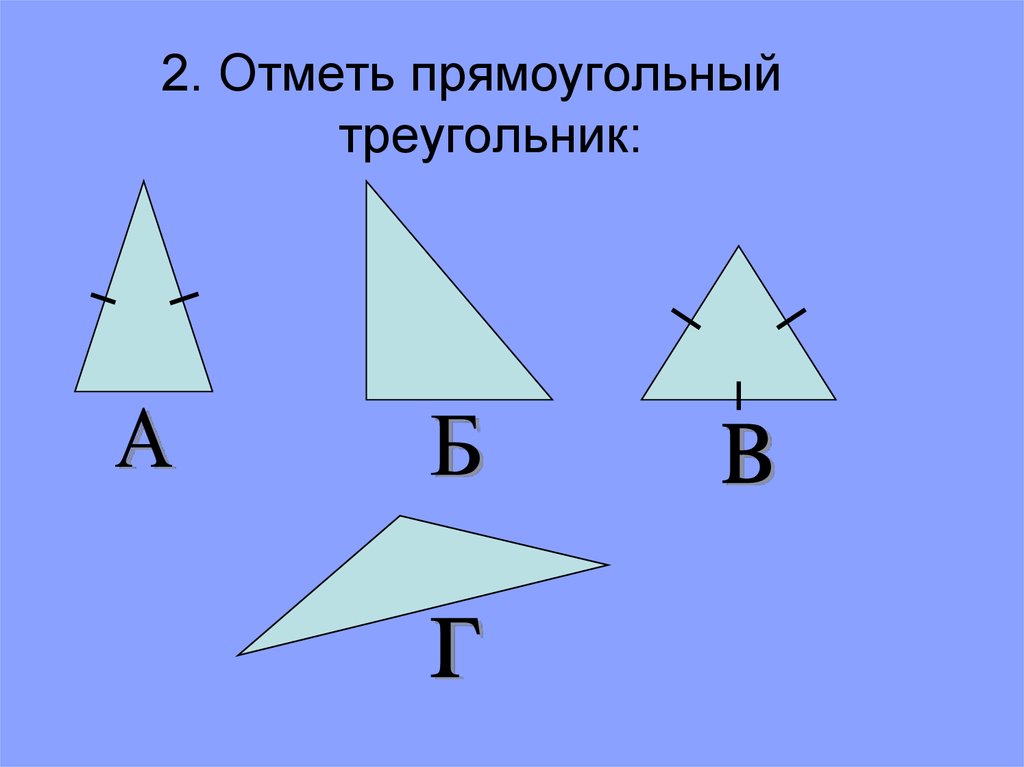
2. Отметь прямоугольныйтреугольник:
4.
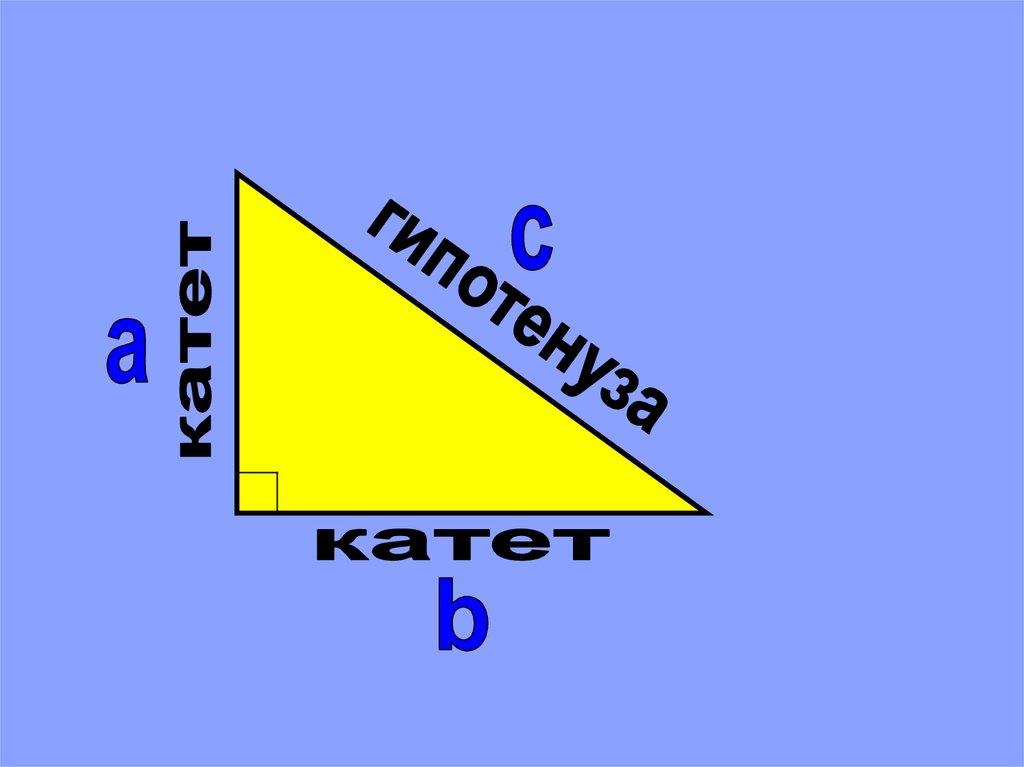
3. Как называются стороны впрямоугольном треугольнике?
А) боковые стороны
Б) основания
В) катеты и гипотенуза
Г) параллельные стороны
5.
4. Один из острых угловпрямоугольного треугольника равен
30°, чему равен другой острый угол?
А) 90°
Б) 60°
В) 30°
С) 180°
6.
5. Выберите формулу площадипрямоугольного треугольника:
1
А) S =2 a·b
1
Б) S =2 a·h
1
B) S = 2 a·b·sin α
Г) S = √ٕp(p-a)(p-b)(p-c)
7.
6. Катет прямоугольноготреугольника, лежащий напротив
угла в 30°, равен 15см. Чему равна
гипотенуза?
А) 15см
Б) 7,5см
В) 20см
Г) 30см
8.
9.
Оценка «5» - все верные ответы.Оценка «4» - 5 верных ответов.
Оценка «3» - 4 верных ответа.
«Надо ещё повторить» - менее 4
верных ответов.
10.
11.
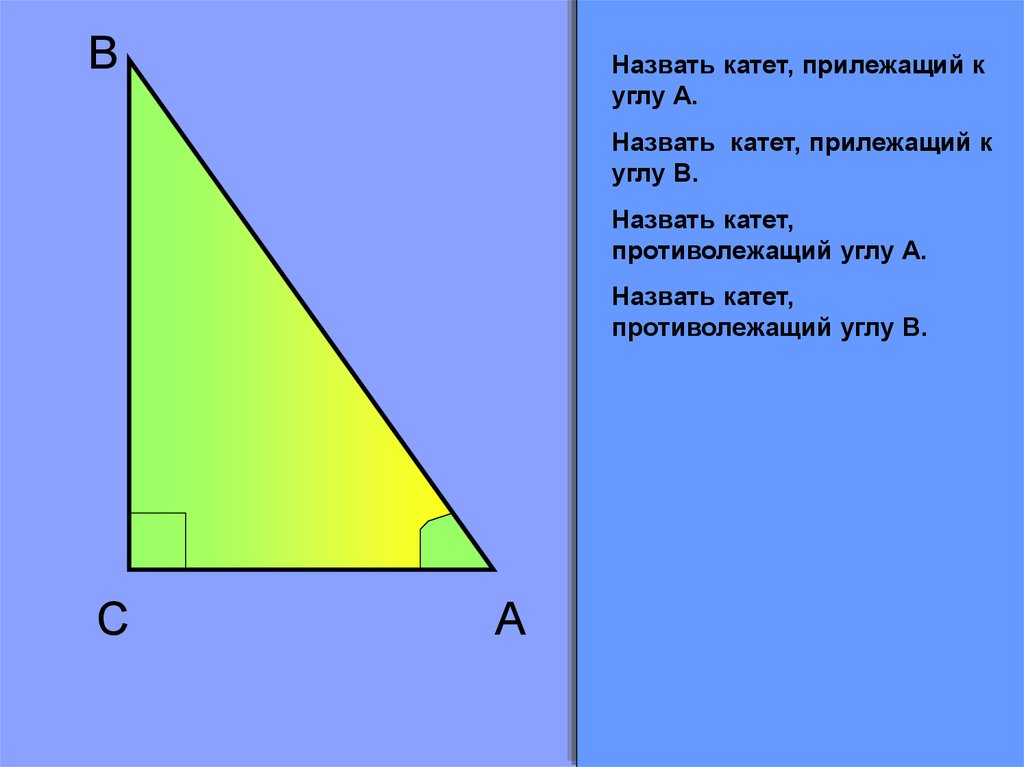
BНазвать катет, прилежащий к
углу А.
Назвать катет, прилежащий к
углу В.
Назвать катет,
противолежащий углу А.
Назвать катет,
противолежащий углу В.
C
A
12.
Синусом острого углапрямоугольного
треугольника
называется
отношение
противолежащего
катета к гипотенузе.
В
С
А
BC
sin A
AB
13.
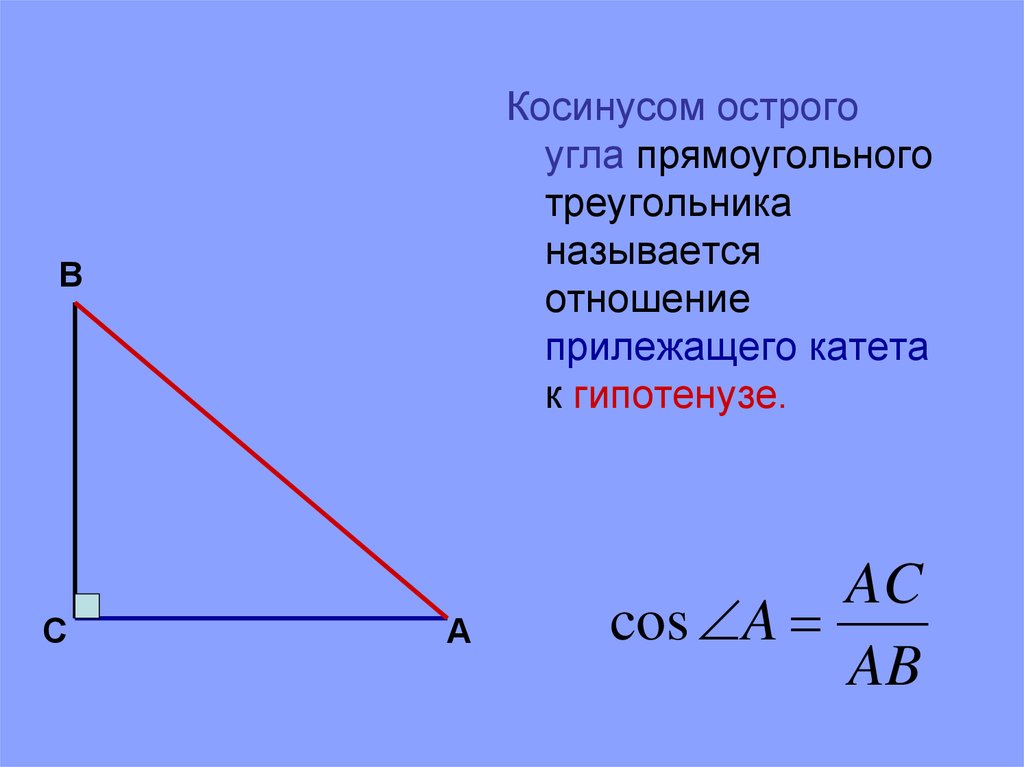
Косинусом острогоугла прямоугольного
треугольника
называется
отношение
прилежащего катета
к гипотенузе.
В
С
А
AC
cos A
AB
14.
Тангенсом острогоугла прямоугольного
треугольника
называется
отношение
противолежащего
катета к
прилежащему.
В
С
А
BC
tg A
AC
15.
16.
17.
18.
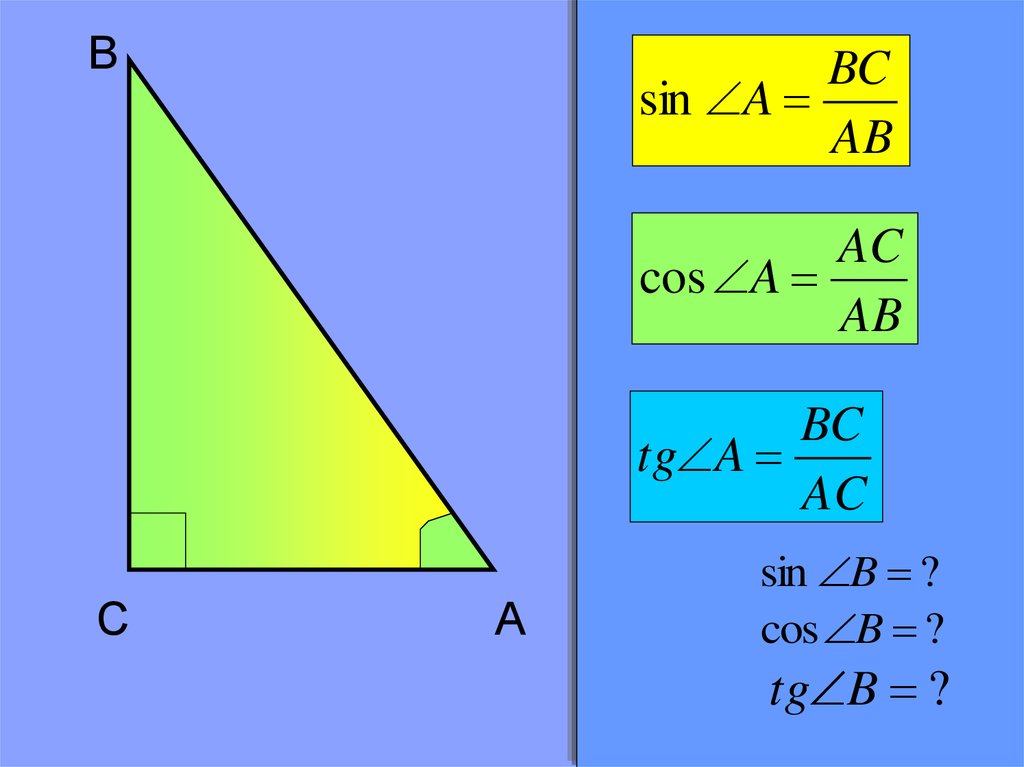
BBC
sin A
AB
AC
cos A
AB
BC
tg A
AC
C
A
sin B ?
cos B ?
tg B ?
19.
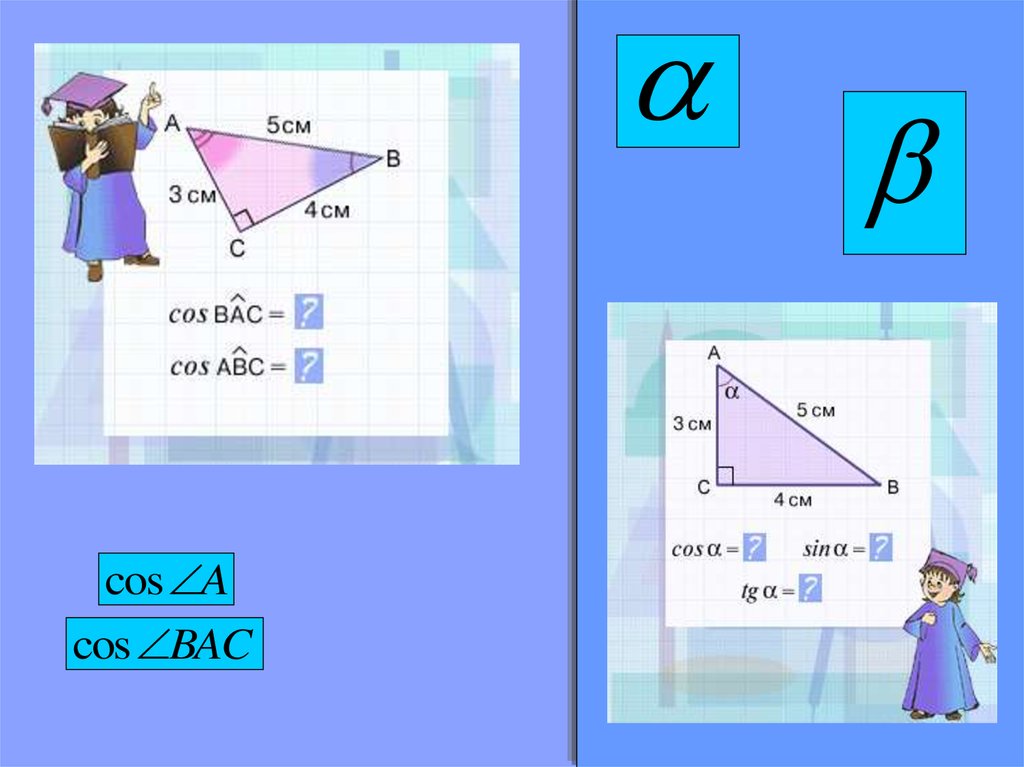
cos Acos BAC
20.
Значение косинусаострого угла
прямоугольного
треугольника не
зависит от величины и
положения
прямоугольного
треугольника.
21.
Найти: 1) sin A, 2) cоs A, 3) tg A, 4) сtg A,Ответ:
В
tg
A=
sin
соs A=
сtg A=
A=
13 см
5
12
12
5
13
512
13
5см
С
А
22.
1.Выполнение домашнего задания начни с изучения§ 4 пункта 66.
2. Повтори определения синуса, косинуса, тангенса и
котангенса острого угла прямоугольного
треугольника.
3. Реши следующие задачи из учебника:
№ 591(а), № 592 (а).
















 Математика
Математика