Соотношения между сторонами и углами прямоугольного треугольника

1.

* СООТНОШЕНИЯ МЕЖДУ
СТОРОНАМИ И УГЛАМИ
ПРЯМОУГОЛЬНОГО
ТРЕУГОЛЬНИКА
1

2.

*
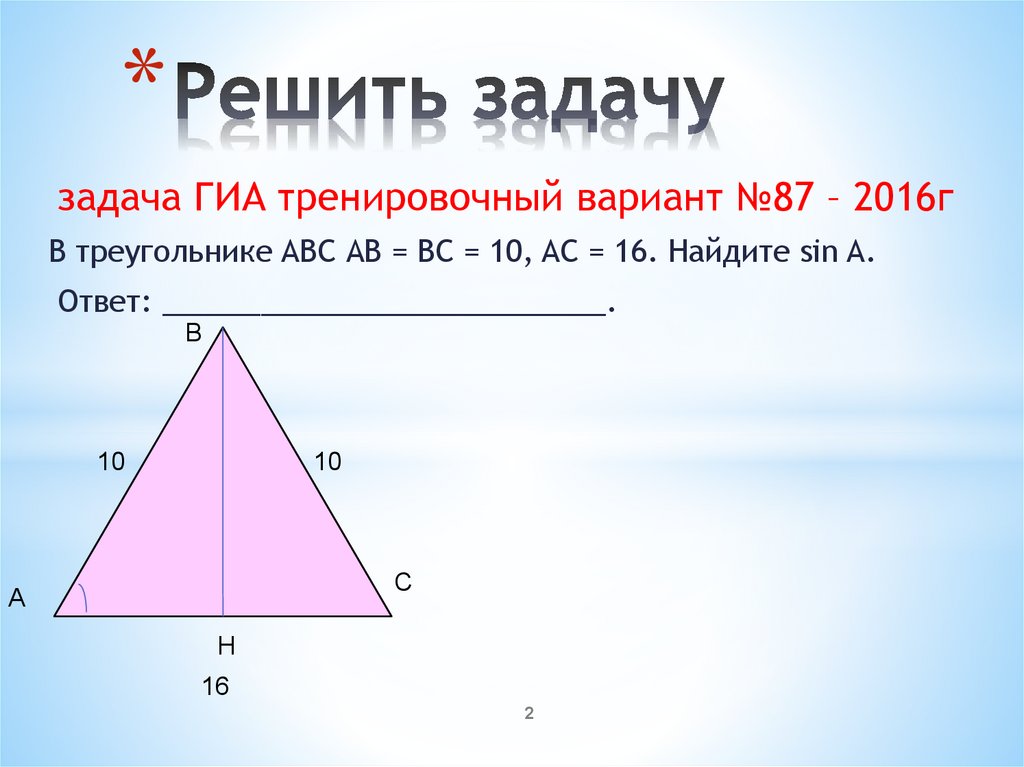
задача ГИА тренировочный вариант №87 – 2016г
В треугольнике ABC АВ = ВС = 10, AC = 16. Найдите sin A.
Ответ: ___________________________.
B
10
10
C
A
H
16
2

3.

«Умение решать задачи –
практическое искусство, подобное
плаванию или катанию на лыжах, или
игре на фортепиано; научиться этому
можно лишь подражая избранным
образцам и постоянно тренируясь».
Дьёрдь Пойа, швейцарский математик
3

4.

4

5.

*
1.Какой треугольник называется
прямоугольным?
2.Назвать стороны
прямоугольного треугольника.
3.Назвать виды углов
прямоугольного треугольника.
4.Что такое отношение?
5

6.

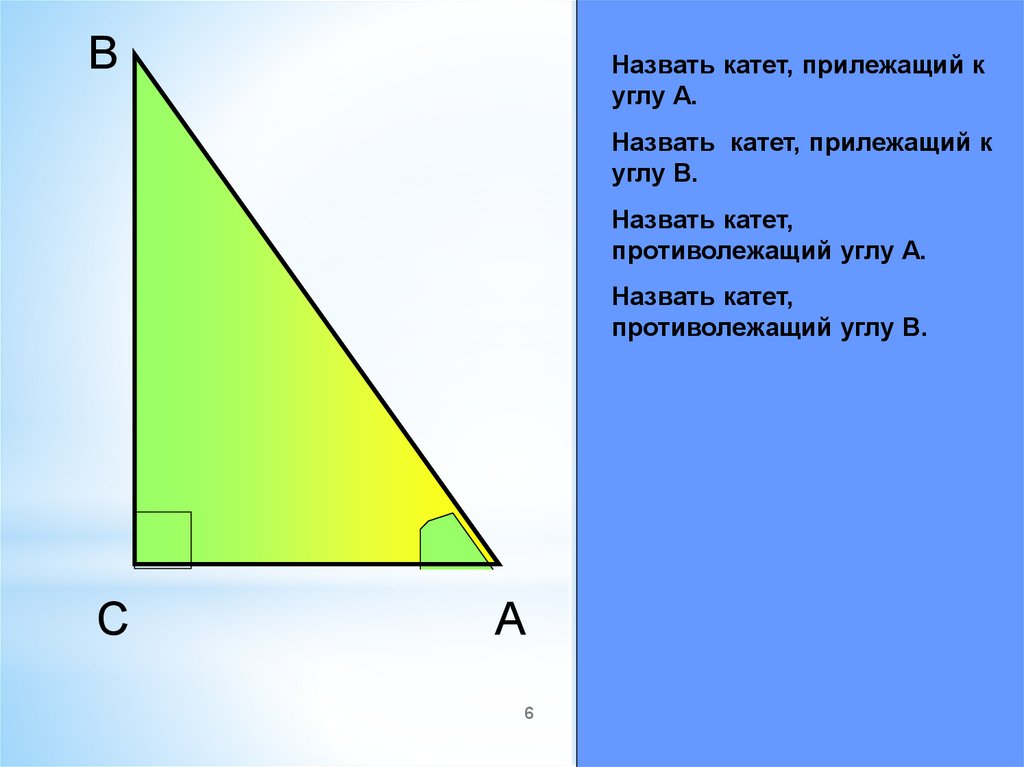
B
Назвать катет, прилежащий к
углу А.
Назвать катет, прилежащий к
углу В.
Назвать катет,
противолежащий углу А.
Назвать катет,
противолежащий углу В.
C
A
6

7.

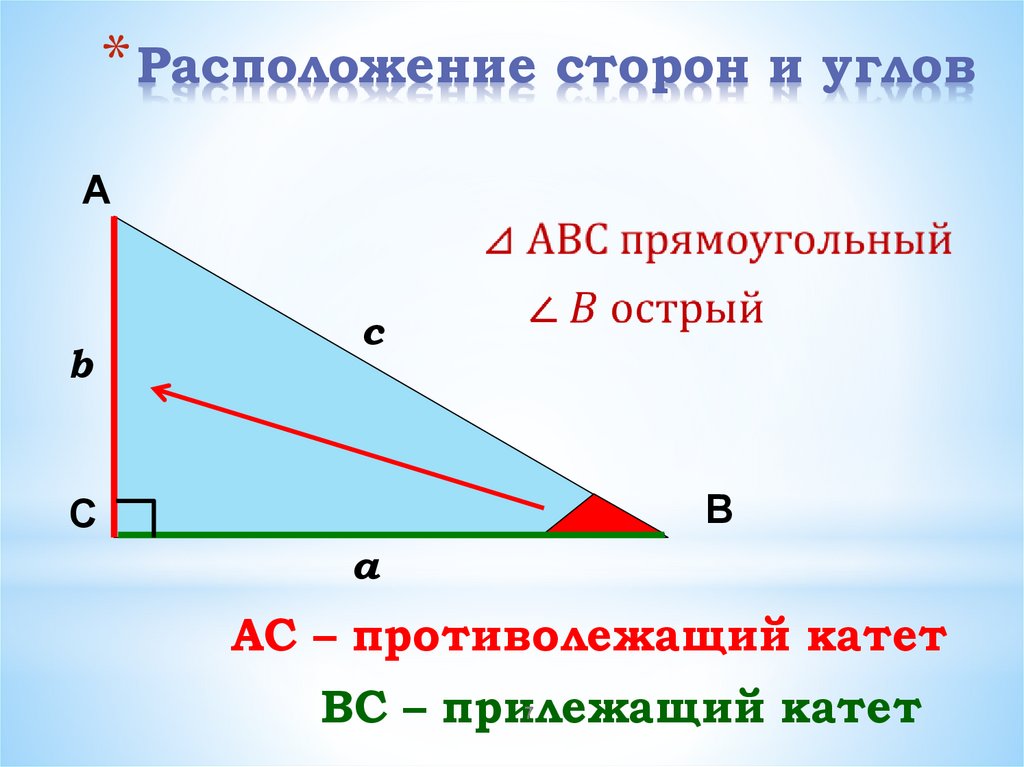
* Расположение сторон и углов
А
b
c
В
С
a
AС – противолежащий катет
ВС – прилежащий катет
7

8.

* Расположение сторон и углов
А
c
b
С
a
В
ВС - противолежащий катет
АС – прилежащий катет
8

9.

*Синус острого угла
А
b
С
sin B
АС b
АВ c
c
В
a
Синусом острого угла в
прямоугольном треугольнике
называется отношение
противолежащего катета к
гипотенузе
9

10.

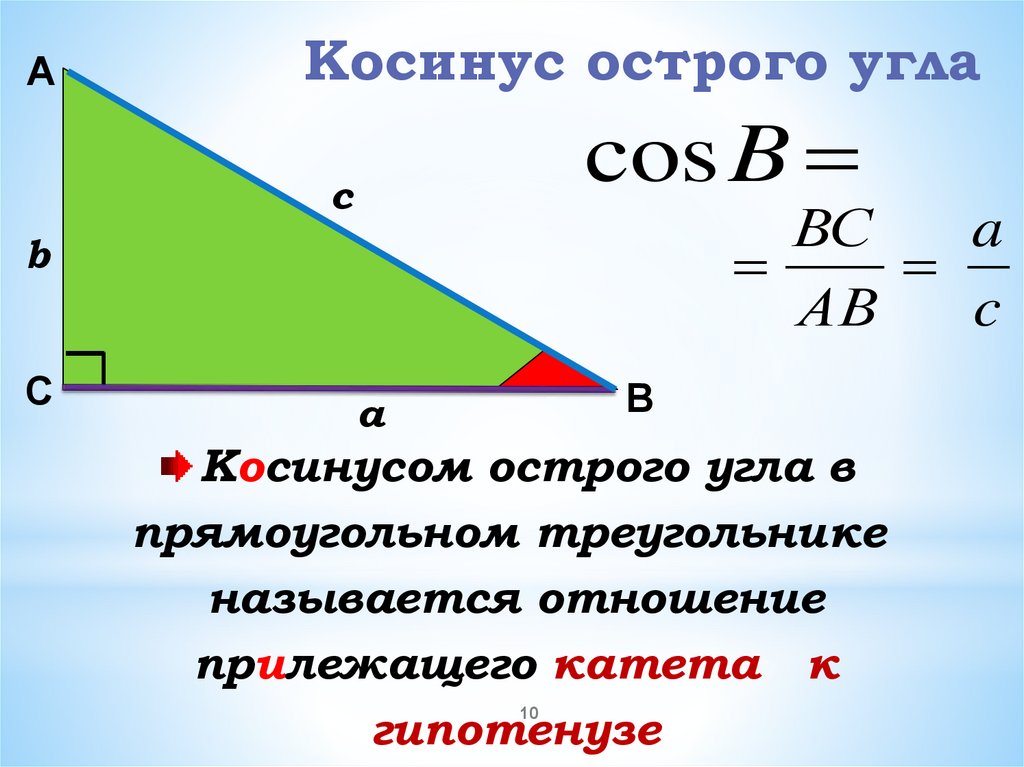
А
Косинус острого угла
cos B
c
ВС
a
АВ
c
b
С
В
a
Косинусом острого угла в
прямоугольном треугольнике
называется отношение
прилежащего катета к
гипотенузе
10

11.

А
b
С
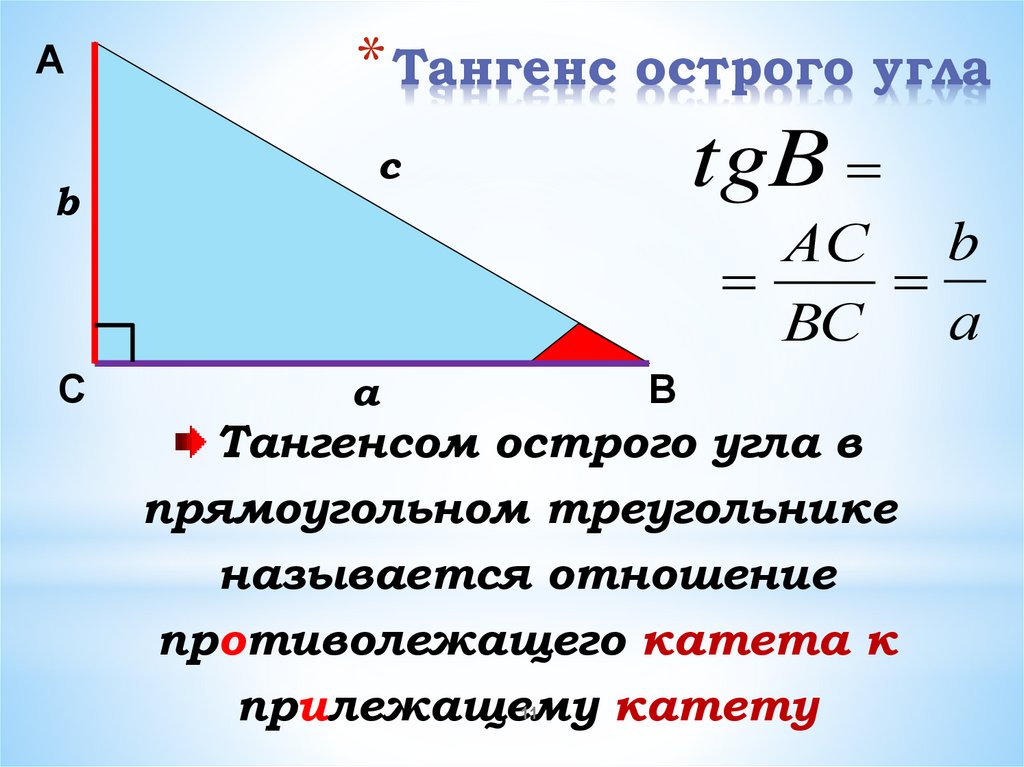
* Тангенс острого угла
tgB
c
АС b
а
ВС
В
a
Тангенсом острого угла в
прямоугольном треугольнике
называется отношение
противолежащего катета к
прилежащему катету
11

12.

*О чем речь?
1. Противоположный катет, острый угол,
sin
отношение, гипотенуза.
2. Прилежащий катет, острый угол,
отношение, противолежащий катет
tg
3. Прилежащий катет, острый угол,
отношение, гипотенуза.
12
cos

13.

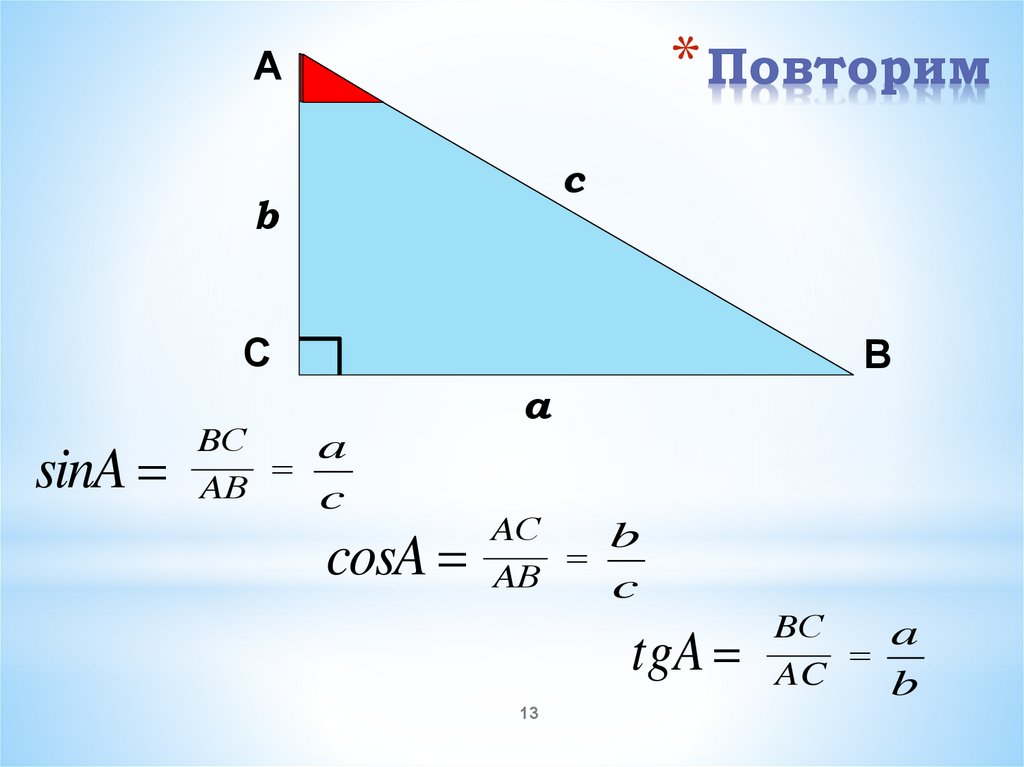
* Повторим
А
c
b
С
В
a
sinA
BС
a
AВ
c
cosA
AС
b
AВ
c
tgA
13
BС
a
AC
b

14.

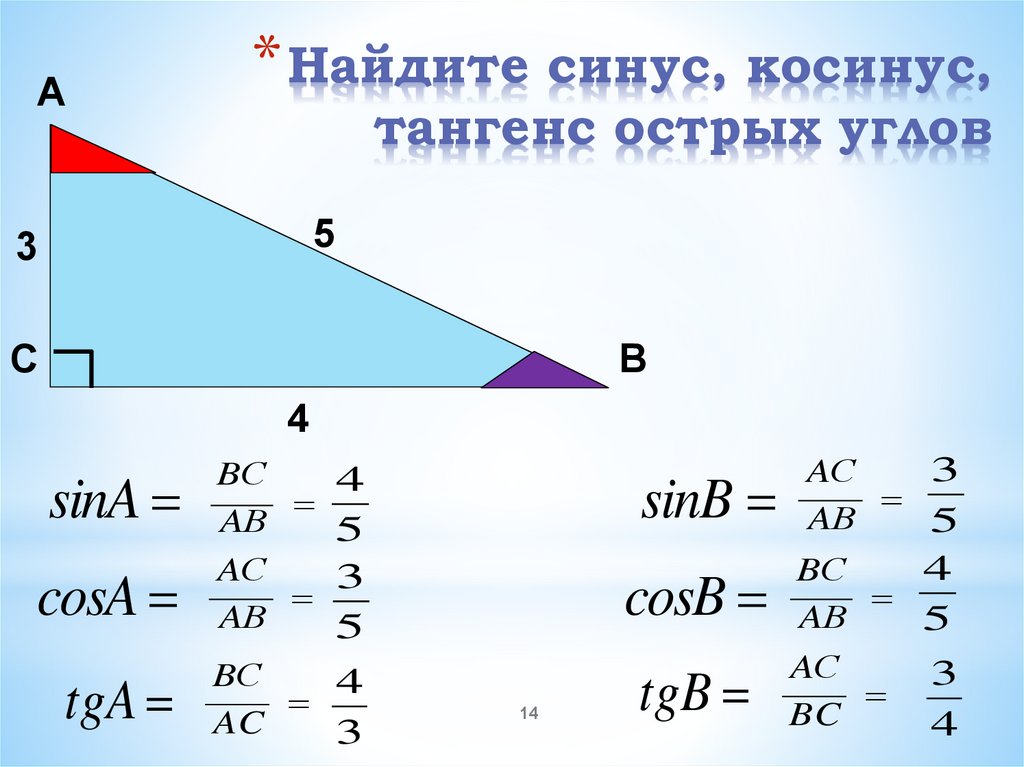
А
* Найдите синус, косинус,
тангенс острых углов
5
3
В
С
4
sinA
cosA
tgA
sinB
BС
4
AВ
5
AС
3
AВ
5
BС
4
AC
3
cosB
14
tgB
3
AС
AВ
5
4
BС
AВ
5
AС
3
BC
4

15.

А
С
Узнаем чему равен
тангенс угла
В
sin A
cos A
BC AC BC AB BC
:
tgA
AB AB AB AC AC
sin B
cos B
AC BC AC AB AС
:
tgB
AB AB AB BC BC
tgA
sin A
cos A
tgB
sin B
cos B
Тангенс угла равен отношению
синуса к косинусу этого угла
15

16.

А
А1
С1
С
В1
В
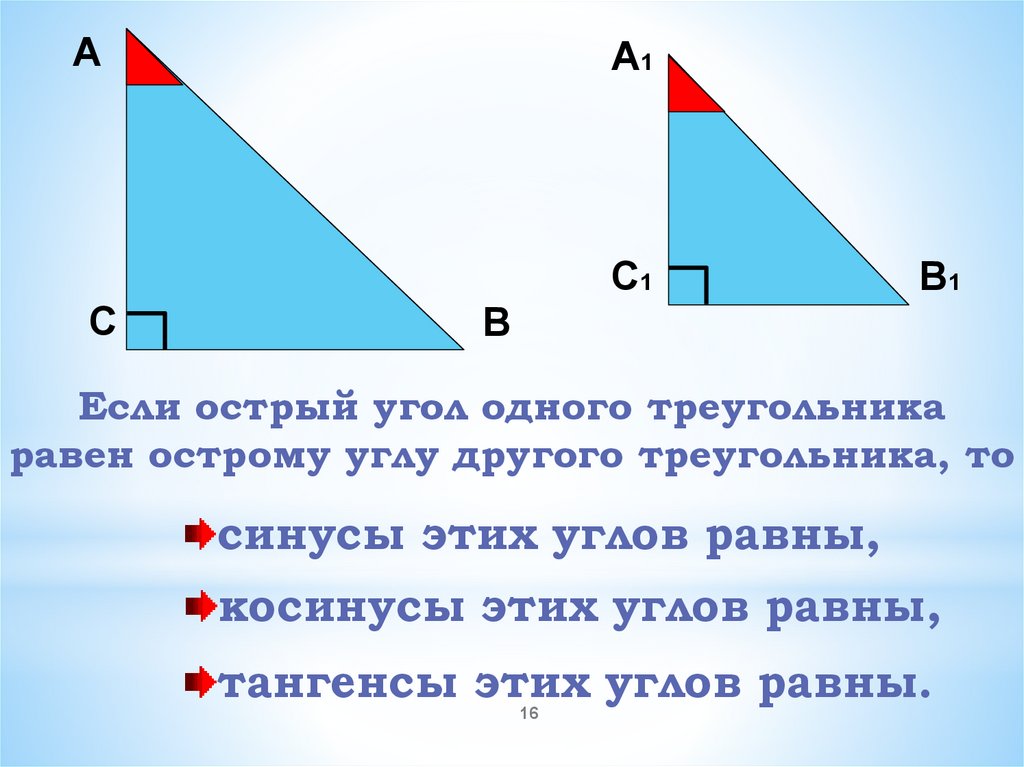
Если острый угол одного треугольника
равен острому углу другого треугольника, то
синусы этих углов равны,
косинусы этих углов равны,
тангенсы этих углов равны.
16

17.

Докажем равенство
А
sin A cos A 1
2
2
В
С
sinA
BС
AВ
cosA
AС
AВ
sin A cos A
2
2
AC
BA AC
BC
AB
1
2
2
2
2
AB
AB
AB
AB
2
2
2
2
17
2

18.

Равенство
sin cos 1
2
2
называется
основным
тригонометрическим
тождеством
18

19.

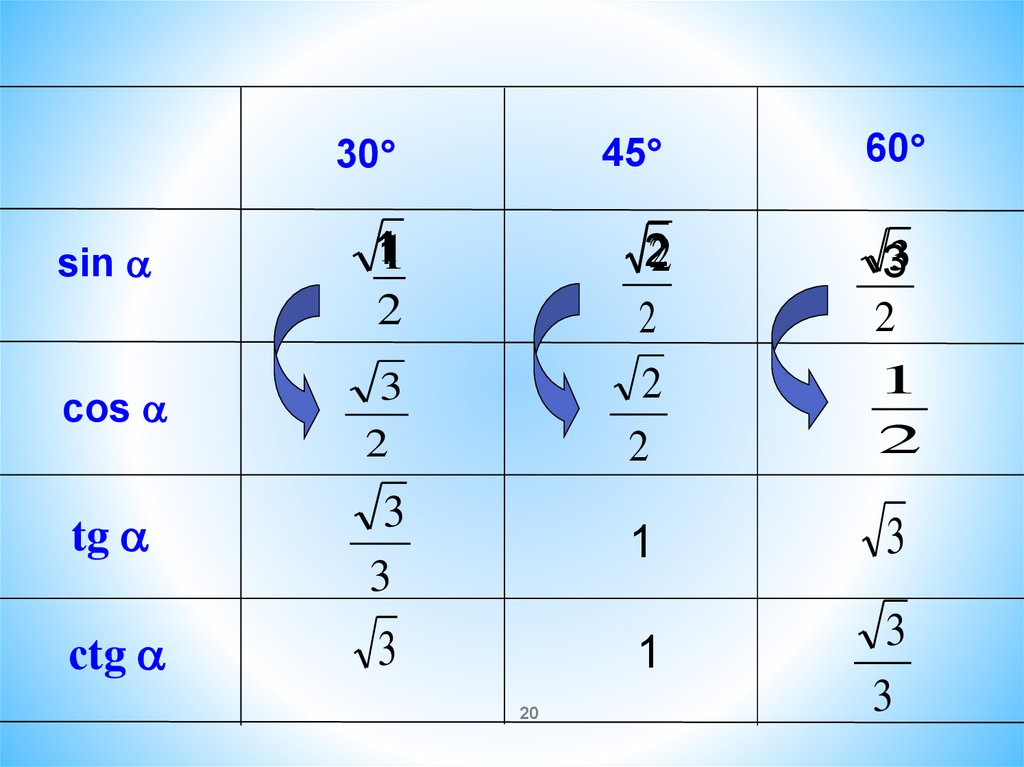
Значение синуса, косинуса
и тангенса для углов 30°,
45°, 60°
19

20.

sin
60
30
45
11
2
222
2
2
2
2
1
2
1
3
1
3
3
cоs
3
2
tg
3
3
сtg
3
20
33

21.

*О чем речь?
1. Противоположный катет, острый угол,
sin
отношение, гипотенуза.
2. Квадрат, прямоугольный треугольник,
гипотенуза, катет.
т. Пифагора
3. Прилежащий катет, острый угол,
tg
отношение, противолежащий катет
4. Половина, гипотенуза, угол, тридцать,
катет.
в
30
катет, против угла
5. Прилежащий катет, острый угол,
cos
отношение, гипотенуза.
26

22.

*Найди ошибку
С
CB
1) sin A
AB
В
2) АВ BC
3) В 67
0
AC
4) cos B
AB
230
А
5) АВ ВС АС
2
27
2
2

23.

Решить:
А
АС= ?
5
3
В
С
4
sin A=
4
5
cos A=
3
5
28
tg A=
4
3

24.

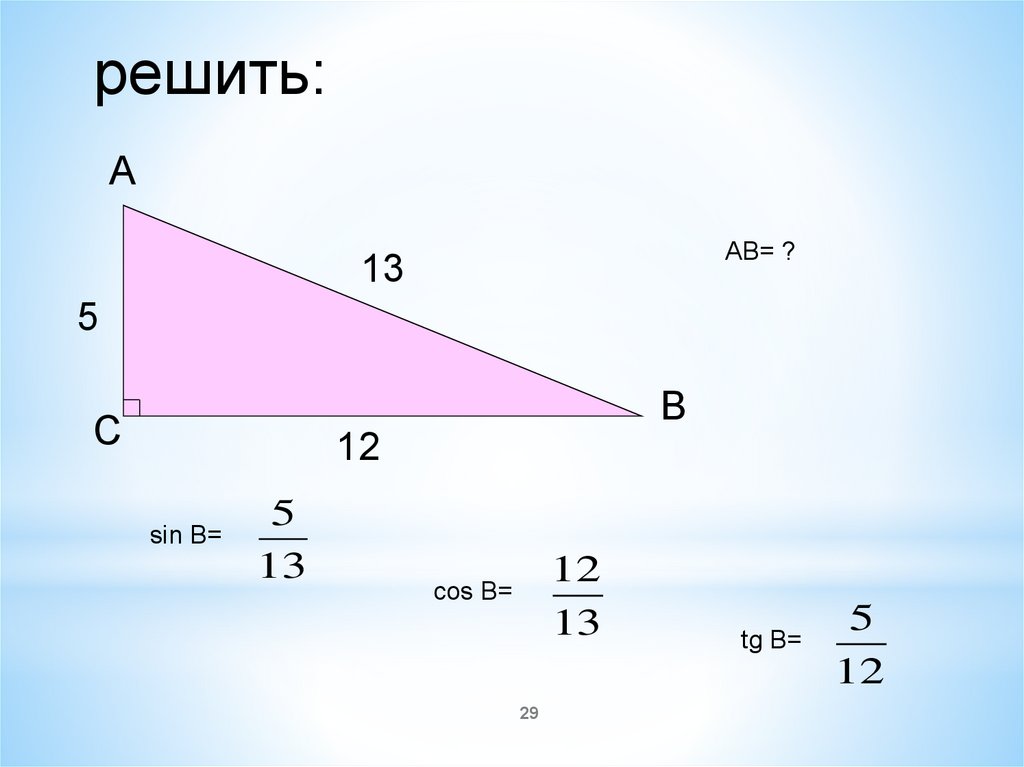
решить:
А
АB= ?
13
5
В
С
12
sin B=
5
13
12
13
cos B=
29
tg B=
5
12

25.

*
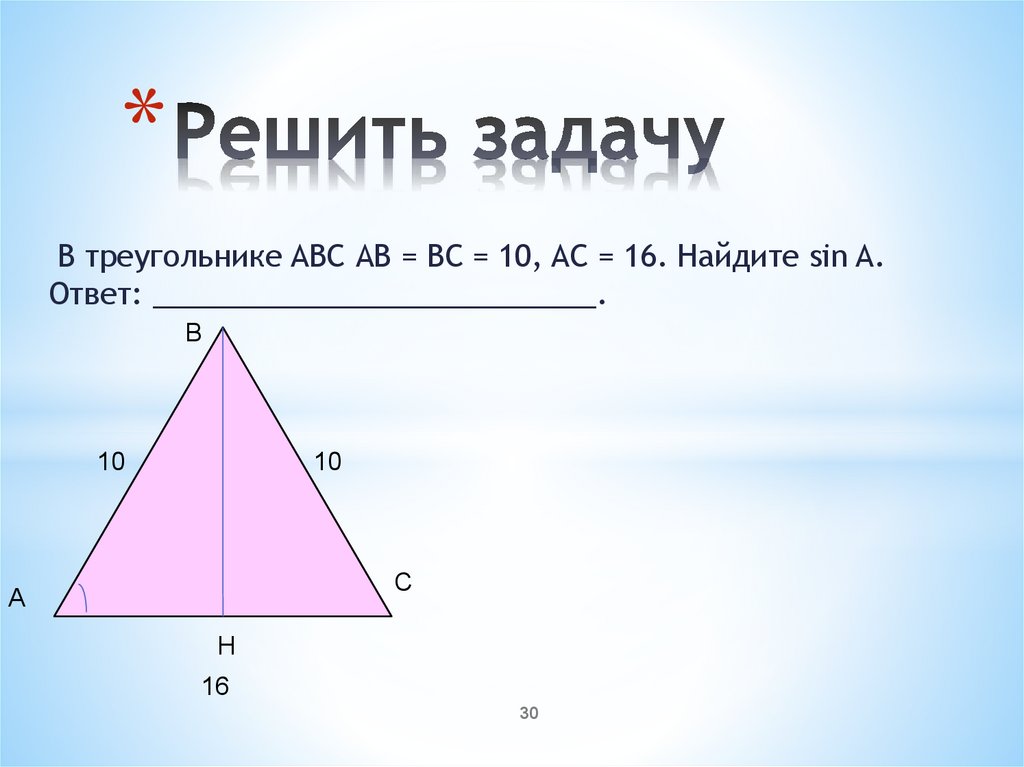
В треугольнике ABC АВ = ВС = 10, AC = 16. Найдите sin A.
Ответ: ___________________________.
B
10
10
C
A
H
16
30

26.

1.
2.
3.
4.
Дайте определение синуса острого угла
прямоугольного треугольника
Дайте определение косинуса острого угла
прямоугольного треугольника
Дайте определение тангенса острого угла
прямоугольного треугольника
Назвать основное тригонометрическое
тождество.
*Оценки за урок.
31

27.

Урок сегодня завершён,
Но каждый должен знать:
Познание, упорство, труд
К прогрессу в жизни приведут!
32

28.

Домашнее задание:
1. § 4 пункт 66, 67.
2. Выучить табличные значения для углов 30 ,
45 , 60 .
3. Решить следующие задачи из учебника: №
591; №593
33

29.

34