Случайность. Потребность в случайных числах

1.

Ревченко Л.П.
учитель информатики
ГОУ школы № 497 Невского района
2019 год

2.

Случайность
Со случайностью мы сталкиваемся на каждом шагу

3.

Всё случайно, непредсказуемо,
НО ...
В универсаме в нужное время должно быть
нужное число кассиров

4.

Телефонная линия должна иметь достаточную
пропускную способность

5.

Непредсказуемо поведение элементарных
частиц в ядерном реакторе, но реакторы
должны надежно работать

6.

Для успешного решения этих
задач и множества других
необходимо уметь:
Получать искусственную последовательность случайных чисел,
успешно заменяющую реальную, определяемую случайными
событиями;
С помощью этой последовательности моделировать случайные
события.

7.

Потребность в случайных числах возникла
давно. Для их получения существует
множество способов:

8.

Таблицы случайных цифр
В 1927 году Л. Триппет опубликовал таблицы, содержащие
свыше 40 000 случайных цифр, произвольно взятых из отчетов
о переписи.
Позже были сконструированы специальные машины,
механически вырабатывающие случайные числа.
Первую такую машину использовали
М. Дж. Кендалл и Б. Бэбингтон-Смит
при создании таблиц из 100 000 случайных цифр.
2057
0762
1429
8535
9029
9745
3458
5023
3502
2436
6435
2646
0295
6177
2755
3080
3275
0521
6623
1133
3278
0500
7573
7426
3188
0187
7707
3047
4901
3519
7888
6411
1631
6981
1972
4269
0022
3860
1580
6751
4022
6540
7804
5528
4690
3586
9839
6641
0404
0735
0888
3504
2651
9051
5764
7155
6489
2660
3341
8784

9.

Как получить таблицу случайных
цифр?
Осуществив N независимых опытов и получив N случайных
цифр, запишем эти цифры (в порядке появления) в таблицу,
получим таблицу случайных цифр.
Таблицы случайных цифр использовали при расчетах вручную.
При расчетах на ЭВМ таблицами не пользовались. Такая таблица
не помещалась во внутреннюю память ЭВМ , а обращение к
внешним ЗУ замедляло счет.

10.

Датчики случайных чисел
С появлением первых ЭВМ начались поиски получения
случайных чисел для использования их в компьютерных
программах.
Поначалу к ЭВМ подключали датчики случайных чисел,
основанные на различных физических эффектах:
шум электронных ламп
излучение радиоактивных веществ и прочее.
Электронный
измеритель уровня
шума с USB
интерфейсом.
Но датчики были слишком медленными, дорогими и
небезопасными. Несовершенство этих методов пробудило
интерес к получению случайных чисел с помощью
арифметических операций самого компьютера.

11.

Джон фон Нейман
(3.12 1903 — 8.02 1957, Будапешт, Вашингтон),
американский математик и физик.
Первым такой подход предложил в 1946 году Джон фон Нейман,
известный как разработчик архитектуры первых ЭВМ.
Идея состояла в том, что нужно только самое первое случайное
число. Дальше применяется следующее рекуррентное правило:
число возводится в квадрат и из результата берется середина.
Таким образом строится последовательность чисел.

12.

Пример получения последовательности
десятизначных случайных чисел
А = 5772156649
- первое число
А2 = 33317792380594909201
33317792380594909201
А=
7923805949 - второе число
А2
=
62786700717407790601
А=
7007174077
А2 = . . .
62786700717407790601
- третье случайное число

13.

Реализация алгоритма фон Неймана
для двузначных чисел
Program numbers;
Var a, b, c, I : integer;
Begin
Writeln(' Генерация двузначных чисел');
Writeln(‘Введите любое двузначное число');
Readln(n);
For i:=10 to 99 do begin
b:=a*a; if b div 1000>0 then c:=b mod 1000 else c:=b;
a:=c div 10;
if (a=1) or (a=2) or (a=3) then a:=a*10;
if a=10 then a:=a+2; if a=60 then a:=a+1;
write (a:5); end; end.

14.

А где же здесь случайность?
Никакой случайности здесь нет. Но получаемые таким
способом числа ведут себя как случайные. Частота
появления любого числа в этой последовательности
примерно одинакова. А в моделировании именно это и надо!
В результате, вместо последовательности случайных чисел
мы имеем ее модель, сохраняющую самое главное свойство:
равномерное распределение вероятностей появления членов
этой последовательности.
Такие последовательности называются псевдослучайными.
Алгоритм получения псевдослучайного числа называется
датчиком случайных чисел.

15.

Продолжение истории
После изобретения Джона фон Неймана математики придумывали
различные датчики случайных чисел.
Проблема в том, что все псевдослучайные последовательности
являются периодическими. Тогда можно ли говорить о
моделировании случайности?
В алгоритме фон Неймана для десятизначных чисел повторяющаяся
последовательность чисел появляется через 1010 операций. Для
человека провести столько опытов дело нескольких лет, а для
компьютера — нескольких часов.
В сложных случаях получения достоверных результатов
моделирования, например, работы ядерного реактора, требуются
датчики с большим периодом (10100).
Разработка быстрых и надежных датчиков случайных чисел
продолжается.

16.

Получение псевдослучайного числа в
программе на Паскале
В более простых случаях моделирования случайных процессов с
успехом применяются имеющиеся в любой системе
программирования алгоритмы получения случайных чисел.
Обычно эти алгоритмы выполнены в виде стандартных функций. В
Паскале - Random.
Примеры использования. Пусть Var A : integer; X : real; . . .
A := RANDOM(N); - получим целое число из интервала [0;N)
A := RANDOM(N) + M; - получим число из интервала [M;N+M)
X := RANDOM; - получим вещественное число из [0;1)
X := C + (D - C)*RANDOM; - получим число из интервала [C;D)
При использовании Random в цикле часто применяют перед
циклом процедуру RANDOMIZE; (изменяет «первое» число)

17.

Одно из применений случайных чисел вычисление площадей и объемов фигур
методом Монте-Карло:
Фигуру, площадь которой нужно найти, поместим в прямоугольник
(квадрат). Будем случайным образом «бросать» точки в этот
квадрат. Естественно, что чем большую площадь в квадрате
занимает фигура, тем чаще в нее будут попадать точки.
Например, во время снегопада количество снежинок, попавших в
круглую песочницу на квадратной детской площадке,
пропорционально площади песочницы.
Обозначим S искомую площадь круглой песочницы;
а=2 — сторона квадрата, содержащего круг;
N — количество случайных точек внутри квадрата;
М — количество точек из числа N, попавших в круг.
Тогда
S = a2 * M/N

18.

Программа определения S и результаты ее работы
2
2
Ответ: S 3.14
Число точек, N
Площадь, S
1000
3.164
5000
3.165
15000
3.141
50000
3.154
100000
3.138

19.

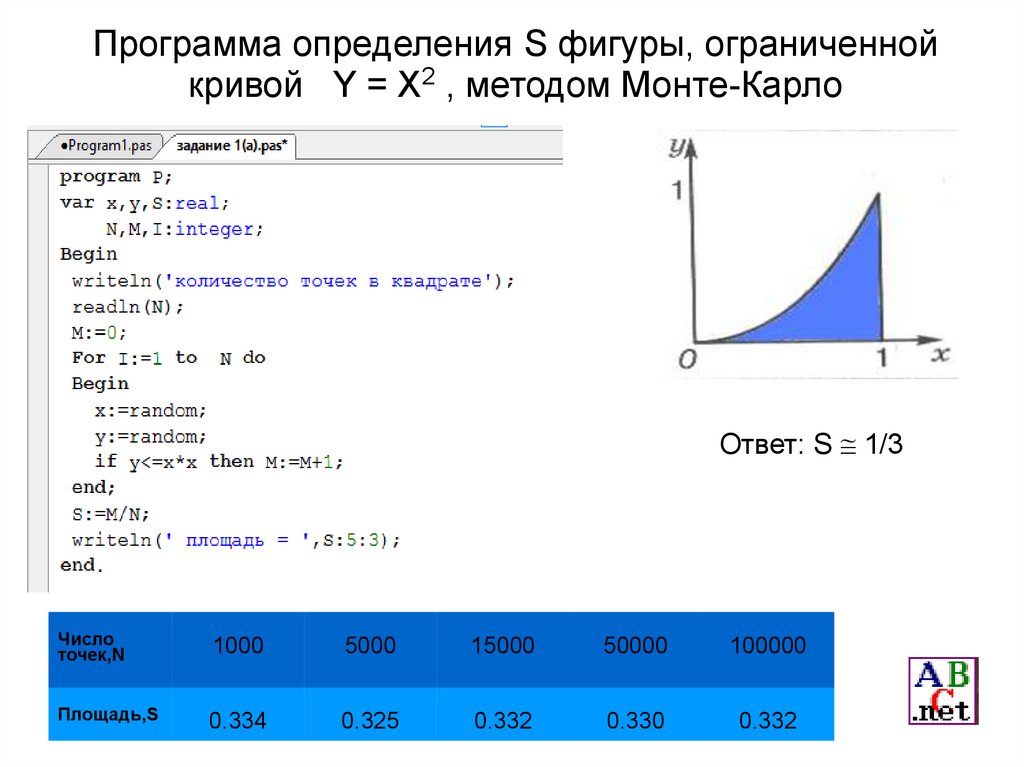
Программа определения S фигуры, ограниченной
кривой Y = X2 , методом Монте-Карло
Ответ: S 1/3
Число
точек,N
1000
5000
15000
50000
100000
Площадь,S
0.334
0.325
0.332
0.330
0.332

20.

Программа определения S фигуры, ограниченной
кривой Y = X3 , методом Монте-Карло
Ответ: S 1/4
Число
точек,N
1000
5000
15000
50000
100000
Площадь,S
0.261
0.241
0.247
0.251
0.251

21.

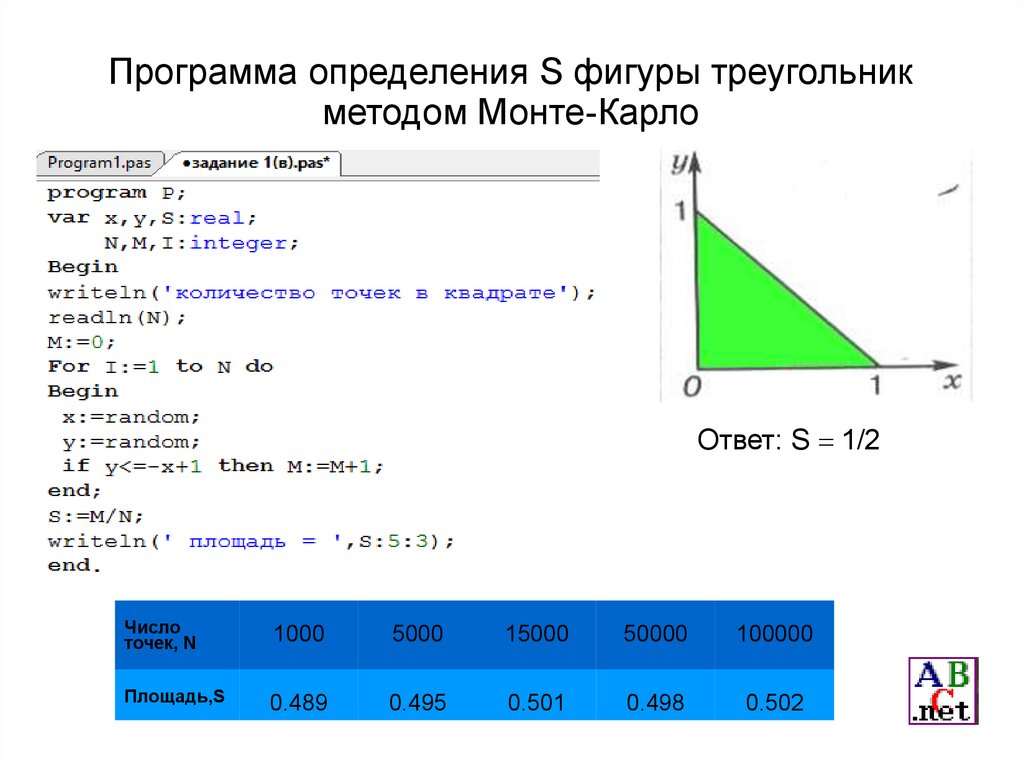
Программа определения S фигуры треугольник
методом Монте-Карло
Ответ: S 1/2
Число
точек, N
1000
5000
15000
50000
100000
Площадь,S
0.489
0.495
0.501
0.498
0.502

22.

Использованы
• учебник для 10 класса «Информатика и ИКТ», авторы: А.Г. Гейн и
др.
• Картинки из Интернета
• Программы с использованием случайных чисел написаны в среде
Pascal ABC.Net.
Систему программирования можно найти на сайте разработчиков
Pascal ABC.Net по ссылке:
http://pascalabc.net/