Похожие презентации:
Принципы моделирования случайных элементов. Базовая случайная величина и методы ее имитации. Лекция 2
1.
Лекция 2.Принципы моделирования случайных
элементов. Базовая случайная
величина и методы ее имитации.
2.
УЧЕБНЫЕ ВОПРОСЫ1. Принципы моделирования случайных элементов. Базовая случайная
величина.
2. Датчики базовой случайной величины.
3.
Вопрос 1.Принципы моделирования случайных
элементов. Базовая случайная величина
4.
На функционирование сложных системоказывают влияние случайные факторы:
управляющие сигналы или воздействия
внешней среды.
При построении имитационной модели
системы возникает необходимость в их
имитации.
5.
Случайной называют такую величину,которая
в
результате
опыта
может
принимать то или иное значение, причем
заранее неизвестно, какое именно, но
известно,
с
какой
вероятностью
принимает это значение.
она
6.
Моделированиена
ЭВМ
любого
случайного элемента (СЭ) подчиняется
двум основным принципам:
1) сходство между СЭ-оригиналом и его
моделью состоит в совпадении (близости)
вероятностных законов распределения
или их числовых характеристик;
2) СЭ определяется ("конструируется")
как функция от простейших СЭ, т.н.
базовых случайных величин.
7.
Базовой случайной величиной (БСВ)называется
непрерывная
случайная
величина (СВ), равномерно распределенная на полуинтервале [0,1).
8.
Функция распределения БСВ:0, если x 0
F x P x x, если 0 x 1
1, если x 1
Fα(x)
1
1
Рис. 1
x
(1.1)
9.
Плотность вероятности БСВ:1, если 0 x 1
f x
0, если x 0,1
fα(x)
1
1
Рис. 2
x
(1.2)
10.
Плотностьчастоту
вероятности
появления
СВ
показывает
в
некоторой
окрестности точки x при многократном
повторении опытов.
11.
Математическое ожидание и дисперсиябазовой случайной величины:
1
M ;
2
1
D M .
12
2
2
(1.3)
12.
Задача моделирования произвольногоСЭ разбивается на два этапа:
1) моделирование на ЭВМ независимых
БСВ α1, α2, …, αr;
2) нахождение функции от этих БСВ
такой,
чтобы
требуемым
модель
законом
СЭ
обладала
распределения
числовыми характеристиками.
и
13.
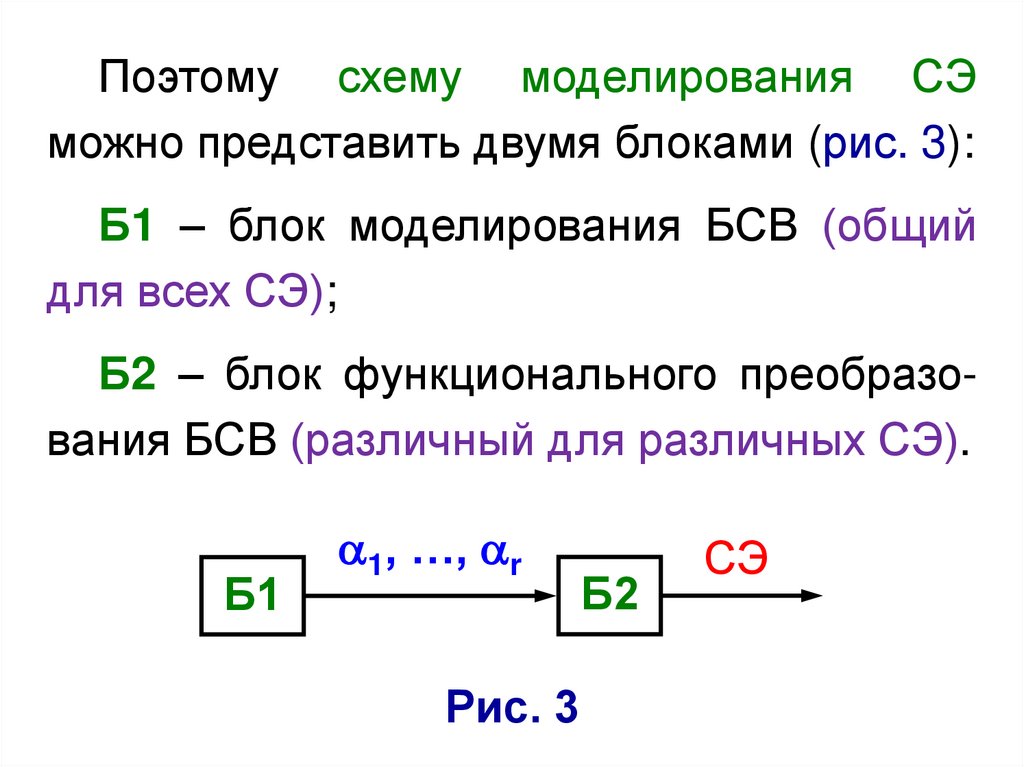
Поэтому схему моделирования СЭможно представить двумя блоками (рис. 3):
Б1 – блок моделирования БСВ (общий
для всех СЭ);
Б2 – блок функционального преобразования БСВ (различный для различных СЭ).
Б1
1, …, r
Рис. 3
Б2
СЭ
14.
Вопрос 2.Датчики базовой случайной величины
2.1. Типы датчиков БСВ
Датчик
БСВ
–
это
устройство,
позволяющее
получать
независимые
реализации БСВ.
Известны 3 типа датчиков БСВ:
табличный, физический, программный.
15.
Табличный датчик БСВ – это таблица,содержащая экспериментально получен-
ные значения СВ, равномерно распределенной в полуинтервале [0,1).
Основной недостаток – нехватка чисел:
часто
для
моделирования
сотни случайных величин.
требуются
16.
Физическийдатчик
БСВ
–
это
радиоэлектронное устройство, состоящее
из
источника
например,
флюктуационного
радиолампы,
шума,
значение
которого является СВ, и нелинейного
преобразователя, рассчитывающего БСВ.
17.
Недостатки физического датчика БСВ:1) невозможность повторения некоторой
ранее полученной реализации БСВ;
2) схемная
нестабильность,
приводя-
щая к необходимости контроля работы
датчика
зовании.
при
очередном
его
исполь-
18.
Программныйдатчик
БСВ
–
это
программа, служащая для имитации на
ЭВМ реализации БСВ.
2.2. Методы построения программных датчиков БСВ
19.
Мультипликативный методi
i ; i i 1 mod M
M
(2.1)
γ – множитель;
M – модуль;
– стартовое значение;
1 1, , M 1
z
z mod M z M – вычет числа z
M по модулю M.
20.
Квадратные скобки означают взятиецелой части.
Пример.
47
47 mod 7 47 7 47 42 5
7
21.
Начинаяс
некоторого
момента,
последовательность {αi*}, а значит и {αi}
повторяется, т.е. датчик имеет период
повторения: Т ≤ M-1.
Параметры γ, M, α1* выбирают из
условия максимума периода.
Период Т можно определить методами
теории чисел или с помощью численных
экспериментов на ЭВМ.
22.
Метод,использующий
линейные
формулы
i
i
;
(2.2)
M
*
*
*
i ( 1 i 1 ... p i p C) mod M
23.
M – модуль;C – приращение;
p – порядок датчика;
γ1, γ2, … , γp – множители;
*
*
*
1 , 2 , , p – стартовые значения.
p
Период датчика Т≤M -1, т.е. растет с
увеличением M и p.
24.
Метод, использующий нелинейныеформулы
i
i
;
M
*
* 2
*
i ( ( i 1 ) i 1 C) mod M
(2.3)
25.
Параметрыэтого датчика целесо-
образно выбирать, исходя из утверждения
следующей теоремы.
Теорема.
q
Если M=2 и q≥2, то наибольший период
последовательности (2.3) достигается, если
β и C – нечетные, γ – четное и выполня-
ется равенство mod 4 1 mod 4 .
26.
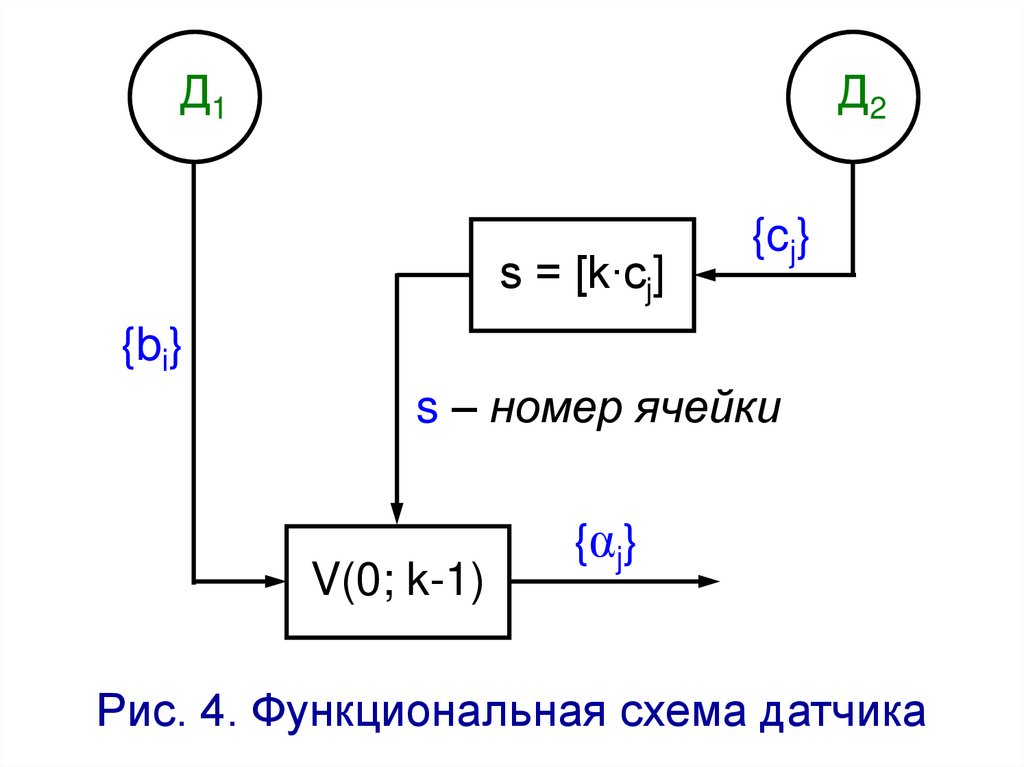
Метод Макларена-МарсальиМетод основан на комбинировании двух
простейших программных датчиков БСВ.
Состав датчика:
датчики Д1 и Д2, формирующие случайные последовательности БСВ {bi} и {cj};
V={v0,v1,…,vk-1} – вспомогательная
таблица для хранения k чисел.
27.
Д1Д2
s = [k∙cj]
{cj}
{bi}
s – номер ячейки
V(0; k-1)
{αj}
Рис. 4. Функциональная схема датчика
28.
Вначале таблица V заполняется элементами последовательности {bi}:vL = bL,
где L=0,…,k-1.
Итоговая БСВ αj (j=0,1,…) является
результатом следующих операций:
s = [k∙cj],
αj = vs,
(2.4)
vs = bj+k,
где [∙] – взятие целой части.
29.
Датчик Д2 осуществляет случайныйвыбор из таблицы V, освобожденная
ячейка которой заполняется случайным
числом от датчика Д1.
Этот
метод
позволяет
ослабить
зависимость между элементами {αj} и
получать очень большие периоды, если
периоды Т1, Т2 последовательностей {bi},
{cj} – взаимно простые числа.



























 Математика
Математика








