Похожие презентации:
Расчет СНС методом перемещений на температуру и осадку опор
1.
Федеральное государственное автономное образовательное учреждениеРОССИЙСКИЙ УНИВЕРСИТЕТ ДРУЖБЫ НАРОДОВ
Лекция №11
РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ
МЕТОДОМ ПЕРЕМЕЩЕНИЙ НА ТЕПЛОВОЕ
ВОЗДЕЙСТВИЕ И ОСАДКУ ОПОР
Ле к т о р :
к . т . н. , д о ц е нт М а р к ови ч А . С.
2.
Расчет методом перемещений на тепловое воздействиеКанонические уравнения метода перемещений для п раз кинематически неопределимых
систем при расчете на тепловое воздействие отличаются от системы уравнений при
расчете методом перемещений на силовое воздействие только свободными членами и
записываются в виде
r11Z1 r12 Z 2 r1n Z n R1,t 0
r21Z1 r22 Z 2 r2n Z n R2,t 0
rn,1Z1 rn,2 Z 2
rn,m Rn Rn,t 0.
Физический смысл приведенной системы уравнений заключается в отсутствии (равенстве
нулю) суммарной реакции в наложенной связи от действия на основную систему
неизвестных и тепловой нагрузки, так как в заданной системе этой наложенной связи нет.
При этом основная система метода перемещений остается такой же, что и при расчете на
силовое воздействие.
3.
Расчет методом перемещений на тепловое воздействиеКак и ранее, будем предполагать, что температура постоянна по длине стержня, а по
толщине нагреваемого элемента изменяется по линейному закону.
В этом случае средняя температура по оси стержня от равномерного нагрева и перепад
температур от неравномерного нагрева определяются по формуле
t1 t2
tср
, t t2 t1.
2
Чтобы вычислить свободные члены Rnt, необходимо построить в статически
неопределимой основной системе метода перемещений грузовую эпюру моментов Mt от
теплового воздействия.
Эта эпюра будет состоять из суммы двух эпюр моментов: эпюры Mt΄ от неравномерного
нагрева стержней и эпюры Mt΄΄ от равномерного нагрева стержней:
M t M t M t .
4.
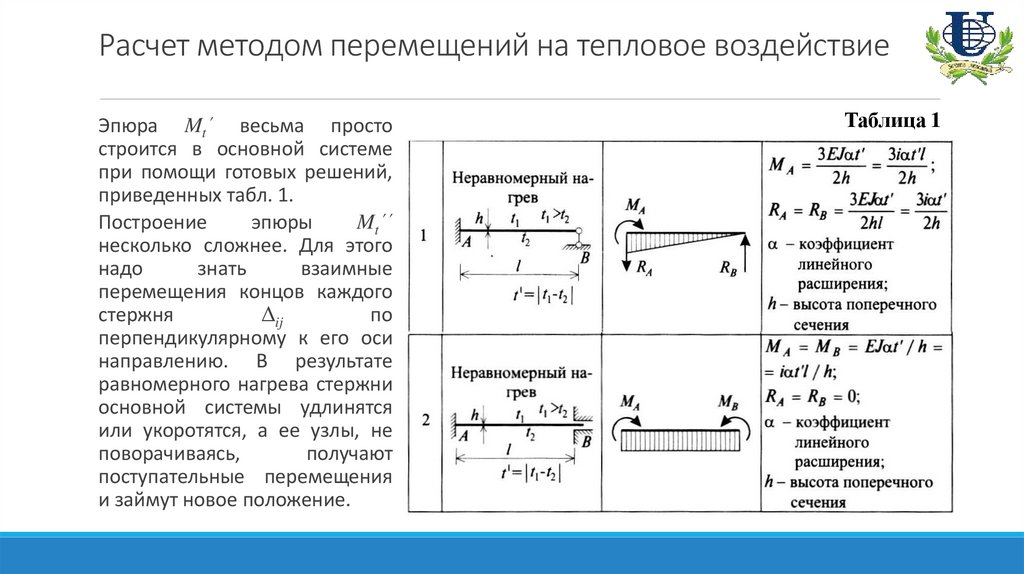
Расчет методом перемещений на тепловое воздействиеЭпюра Mt΄ весьма просто
строится в основной системе
при помощи готовых решений,
приведенных табл. 1.
Построение
эпюры
Mt΄΄
несколько сложнее. Для этого
надо
знать
взаимные
перемещения концов каждого
стержня
Δij
по
перпендикулярному к его оси
направлению. В результате
равномерного нагрева стержни
основной системы удлинятся
или укоротятся, а ее узлы, не
поворачиваясь,
получают
поступательные перемещения
и займут новое положение.
Таблица 1
M t M t M t .
5.
Расчет методом перемещений на тепловое воздействиеУдлинение или укорочение i-го стержня основной системы определяется по известной из
формуле
i tсрl ,
где α – коэффициент линейного расширения материала, l – длина нагреваемого стержня.
Из приведенных выше рассуждений следует, что для построения эпюры Mt΄ нужно сначала
построить новое положение узлов основной системы с величинами их смещений и
изобразить деформации искривленных стержней. После этого в новой схеме основной
системы следует перенести на деформированные стержни готовые эпюры моментов из
таблицы, ординаты которых надо умножить на соответствующие значения Δij.
Так, для балки, защемленной на одном конце и шарнирно опертой на другом, эпюра
моментов представляет собой треугольник с ординатой в защемлении, равной
M t
3EJ
l
2
ij .
6.
Расчет методом перемещений на тепловое воздействиеДля балки, защемленной с двух концов, эпюра моментов будет представлять собой
равнобокую перекрученную трапецию с моментами по концам, равными
M t
6 EJ
l
2
ij .
Напомним, что Δij – взаимное перемещение концов каждого стержня в основной системе
по направлению, перпендикулярному к оси стержня.
Полученная таким образом эпюра моментов и есть эпюра Mt΄΄.
Окончательная грузовая эпюра Mt в основной системе строится по формуле
M t M t M t .
Заметим, что свободные члены Rnt можно вычислить не только по единой эпюре Мt, но и
отдельно с помощью эпюр Mt΄ и Mt΄΄ по следующей формуле:
Rn,t Rn ,t Rn ,t ,
7.
Расчет методом перемещений на тепловое воздействиегде Rt΄ – реакция во введенной связи от неравномерного нагрева, а Rt΄΄ – реакция в той же
связи от равномерного нагрева.
После вычисления всех коэффициентов, решения системы канонических уравнений и
нахождения неизвестных Z1, Z2, ..., Zn окончательная эпюра изгибающих моментов для
заданной системы строится по формуле
M M1Z1 M 2 Z 2
M nZn M t .
Наряду с обычными проверками окончательной эпюры моментов, полученной в результате
расчета заданной системы методом перемещений на тепловое воздействие (равенство
нулю реакций во введенных связях), возможна проверка перемножением окончательной
эпюры М с любой единичной Mn, или суммарной единичной эпюрой MΣ построенными в
основной системе метода перемещений:
l
MiM
EJ dx 0,
0
l
M M
EJ dx 0.
0
Последние уравнения следуют из теоремы Бетти о взаимности работ.
8.
Расчет методом перемещений на тепловое воздействиеПоследовательность расчета
систем
методом
перемещений при тепловом
воздействии
сохраняется
такой же, как и при силовом
воздействии.
В
качестве
примера
рассмотрим
дважды
кинематически
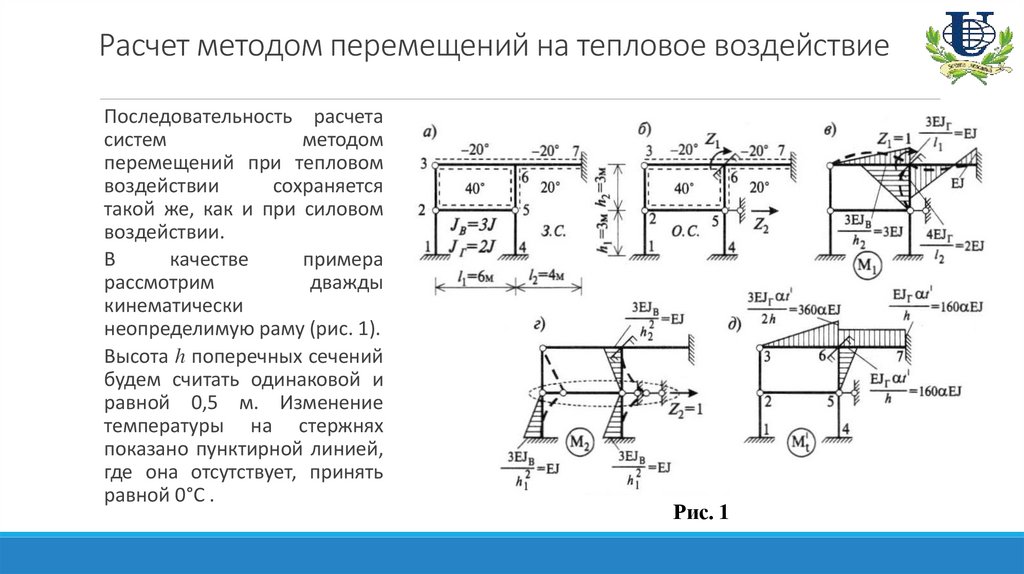
неопределимую раму (рис. 1).
Высота h поперечных сечений
будем считать одинаковой и
равной 0,5 м. Изменение
температуры на стержнях
показано пунктирной линией,
где она отсутствует, принять
равной 0°С .
Рис. 1
9.
Расчет методом перемещений на тепловое воздействиеДля определения неизвестных запишем систему уравнений:
r11Z1 r12 Z 2 R1,t 0
r21Z1 r22 Z 2 R2,t 0.
Единичные эпюры M1 и М2 представлены на рис. 1 в, г. Эпюра моментов Mt΄ от
неравномерного нагрева стержней строится при помощи таблицы и имеет вид,
показанный на рис. 1 д.
Для построения эпюры Mt΄΄ от равномерного нагрева сначала найдем удлинения
стержней рамы:
стойки 2-3: 1 tср h2 60 , стойки 5-6: 2 tср h2 90 ,
ригеля 2-5: 3 tср l1 120 ,
ригеля 3-6: 4 tср l1 60 .
Ригель 6-7 не удлиняется, так как средняя температура по оси стержня равна нулю.
10.
Расчет методом перемещений на тепловое воздействиеНовое положение узлов основной системы после равномерного нагрева изображено на
рис. 2 а, с помощью которого определим величины взаимных смещений концов каждого
стержня Δij по направлению, перпендикулярному к оси стержня:
12
33 120
120 ,, 23 3 4 60 ,
12
36 2 1 30 ,
67 2 90 .
После нахождения Δij строим эпюру моментов Mt΄΄ (рис. 2 б).
После построения эпюр Mt΄ и Mt΄΄ строим окончательную грузовую эпюру моментов Mt в
основной системе (рис. 2, в), по которой определяются свободные члены Rit, точно так же,
как и по эпюре МР от силового воздействия.
По эпюрам M1 , М2, Mt определим реактивные моменты и реактивные усилия:
r11 EJ 2 EJ 3EJ 6 EJ , r12 r21 EJ , r22 EJ ,
R1t EJ 365 227,5 180 42,5 EJ , R2t EJ 60 40 100 EJ .
11.
Расчет методом перемещений на тепловое воздействиеПосле
подстановки
единичных
коэффициентов и свободных членов в
канонические уравнения и почленного
их деления на EJ получим:
6Z1 Z 2 42,5 0
Z1 Z 2 100 0.
Из
решения
системы
значения неизвестных:
находим
Z1 11,5 , Z 2 111,5 .
Строим исправленные единичные
эпюры моментов M1Z1 и M2Z2 (рис. 2 г,
д), а затем строим окончательную
эпюру М для заданной системы от
теплового воздействия (рис. 3 а).
Рис. 2
12.
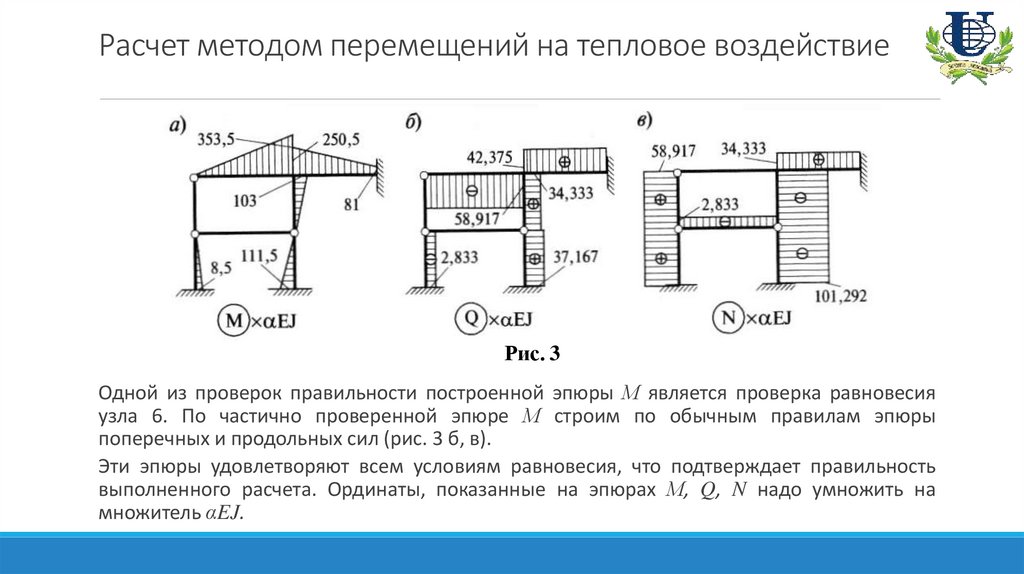
Расчет методом перемещений на тепловое воздействиеРис. 3
Одной из проверок правильности построенной эпюры М является проверка равновесия
узла 6. По частично проверенной эпюре М строим по обычным правилам эпюры
поперечных и продольных сил (рис. 3 б, в).
Эти эпюры удовлетворяют всем условиям равновесия, что подтверждает правильность
выполненного расчета. Ординаты, показанные на эпюрах М, Q, N надо умножить на
множитель αEJ.
13.
Расчет методом перемещений на осадку опорОсновная система метода перемещений при расчете рам и балок на осадку опор остается
такой же, как и при расчете на силовое и тепловое воздействия. Канонические уравнения
для п раз кинематически неопределимых систем отличаются от ранее рассматриваемых
систем уравнений только свободными членами и записываются в виде
r11Z1 r12 Z 2 r1n Z n R1,c 0
r21Z1 r22 Z 2 r2 n Z n R2,c 0
rn,1Z1 rn,2 Z 2
rn,m Rn Rn,c 0.
Физический смысл любого уравнения системы аналогичен тому, как он формулировался
при других воздействиях. Свободные члены канонических уравнений Rn,c – реакции во
введенных дополнительных связях от кинематического воздействия. Для их вычисления
нужно построить в основной системе грузовую эпюру Мс от заданного смещения опор.
14.
Расчет методом перемещений на осадку опорПрежде чем строить эпюру Мс надо в основной системе показать новое положение узлов,
вызванное смещением опор, изобразить деформации стержней и определить
поступательные перемещения их концов по перпендикулярному к ним направлению.
Эта процедура аналогична той, которая применялась при построении эпюры Mt΄΄ от
равномерного нагрева стержней. После этого эпюра Мс весьма просто строится путем
перенесения на деформированные стержни основной системы соответствующих эпюр
моментов из приведенной ранее таблицы, ординаты которых нужно умножить на
найденные значения взаимных смещений концов стержней.
Определив все коэффициенты, входящие в систему канонических уравнений, получив
значения искомых перемещений узлов, окончательную эпюру изгибающих моментов в
заданной системе от смещения опор довольно просто построить по формуле
M M1Z1 M 2 Z 2
M n Zn M c.
Проверка правильности окончательной эпюры М заключается в равенстве нулю реакций
во введенных связях.
15.
Расчет методом перемещений на осадку опорЕсли решение задачи ведется с точностью до масштабного множителя EJ, то числа
получаются малыми, поэтому, чтобы избежать больших расхождений в окончательных
значениях изгибающих моментов в узлах, необходимо учитывать при расчете большое
число знаков после запятой.
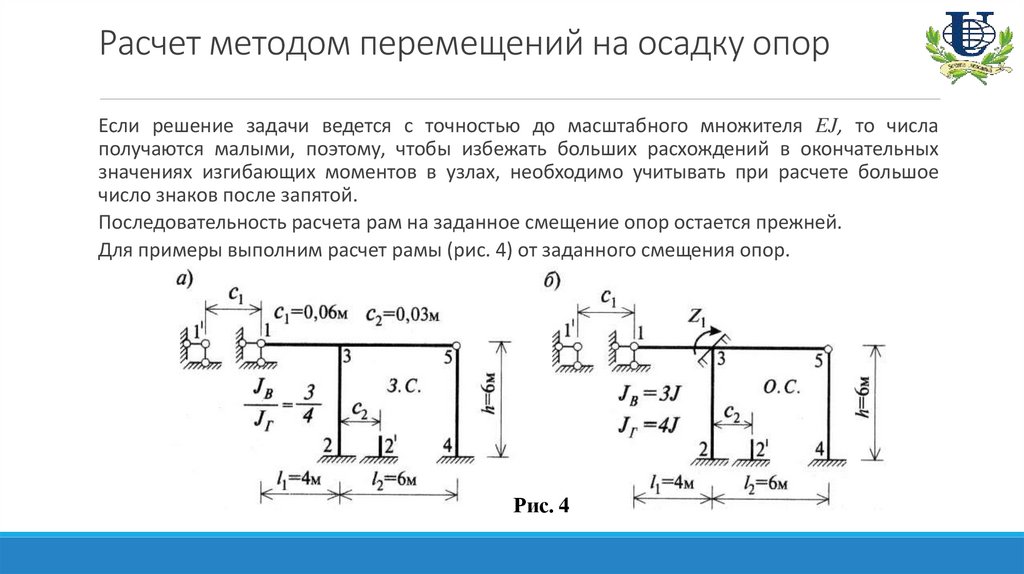
Последовательность расчета рам на заданное смещение опор остается прежней.
Для примеры выполним расчет рамы (рис. 4) от заданного смещения опор.
Рис. 4
16.
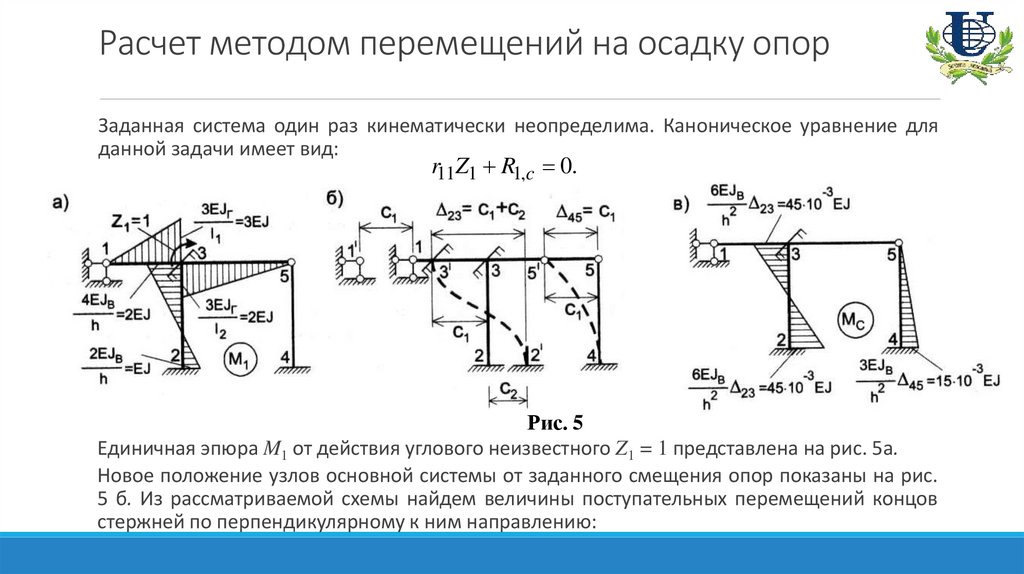
Расчет методом перемещений на осадку опорЗаданная система один раз кинематически неопределима. Каноническое уравнение для
данной задачи имеет вид:
r11Z1 R1,c 0.
Рис. 5
Единичная эпюра M1 от действия углового неизвестного Z1 = 1 представлена на рис. 5а.
Новое положение узлов основной системы от заданного смещения опор показаны на рис.
5 б. Из рассматриваемой схемы найдем величины поступательных перемещений концов
стержней по перпендикулярному к ним направлению:
17.
Расчет методом перемещений на осадку опор23 с1 с2 0,09м, 45 с1 0,06м.
Эпюру изгибающих моментов Мс в основной системе строим при помощи таблицы.
Для стержня 2-3 табличные ординаты моментов надо умножить на величину Δ23, а
для стержня 4-5 - на величину Δ45 (рис. 5 в).
По эпюрам М1 и Мс вычисляем коэффициенты r11, R1c:
r11 EJ (3 2 2) 7 EJ , R1c 0,045EJ .
Из решения канонического уравнения найдем значение для неизвестного Z1:
R1c
Z1
6, 429 10 3 рад.
r11
Окончательную эпюру моментов (рис. 6 б) получаем по формуле
M M1Z1 M c ,
где M1Z1 – исправленная единичная эпюра моментов (рис. 6 а).
18.
Расчет методом перемещений на осадку опорРис. 6
Все ординаты моментов, показанные на рис. 6 б, нужно умножить на множитель 10-3 EJ.
Относительная погрешность в равновесии узла 3 составляет менее 0,01%.













 Механика
Механика








