Метод перемещений

1.

Санкт-Петербургский государственный
архитектурно-строительный университет
кафедра строительной механики
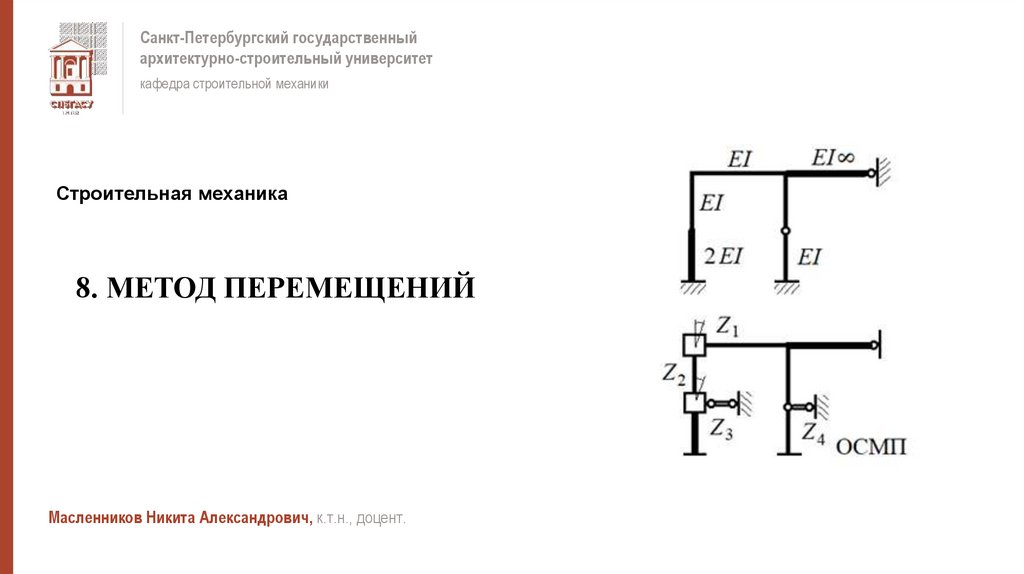
Строительная механика
8. МЕТОД ПЕРЕМЕЩЕНИЙ
Масленников Никита Александрович, к.т.н., доцент.

2.

Кафедра строительной механики
Направление 8.03.01 – Строительство.
Часть 2. Лекция 18. (2).
8. МЕТОД ПЕРЕМЕЩЕНИЙ
8.2. Примеры расчёта дважды кинематически неопределимых рам и
балок методом перемещений.

3.

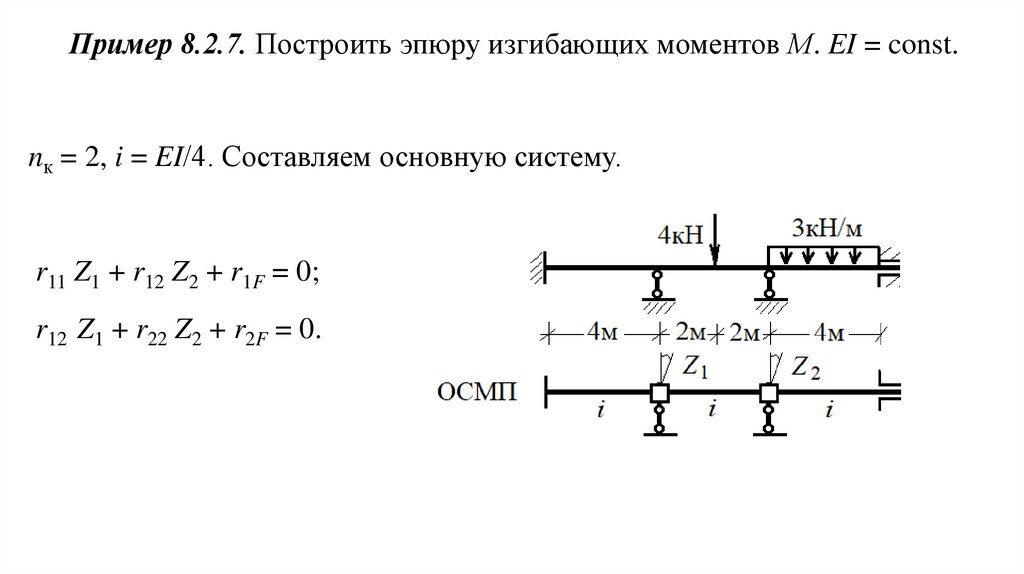
Пример 8.2.7. Построить эпюру изгибающих моментов М. EI = const.
nк = 2, i = EI/4. Составляем основную систему.
r11 Z1 + r12 Z2 + r1F = 0;
r12 Z1 + r22 Z2 + r2F = 0.

4.

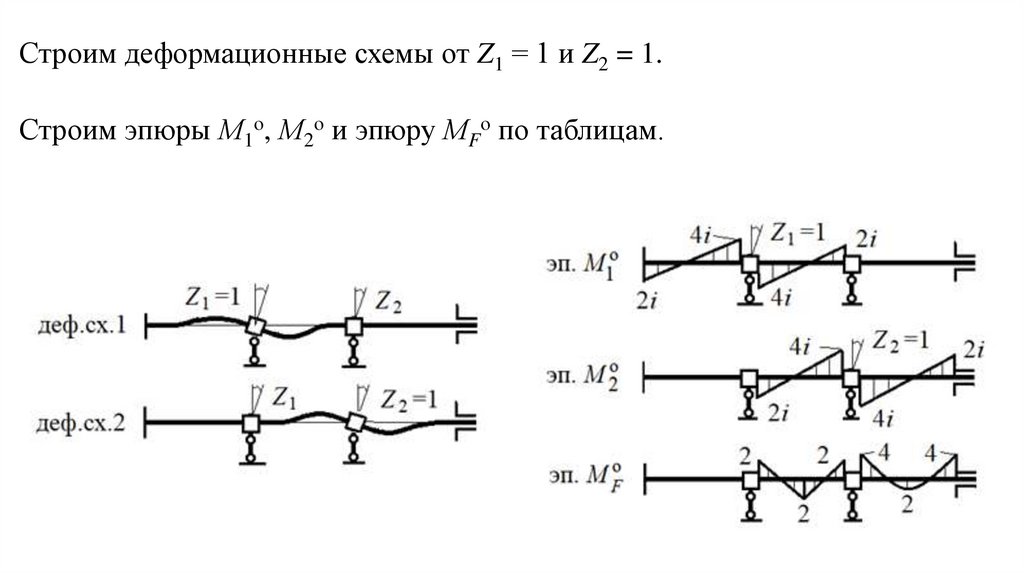
Строим деформационные схемы от Z1 = 1 и Z2 = 1.
Строим эпюры М1о, М2о и эпюру МFо по таблицам.

5.

Определяем реакции в дополнительных связях.
Решаем уравнения: 8i Z1 + 2i Z2 – 2 = 0;
2i Z1 + 8i Z2 – 2 = 0.
Z1 = Z2 = 0,2/i

6.

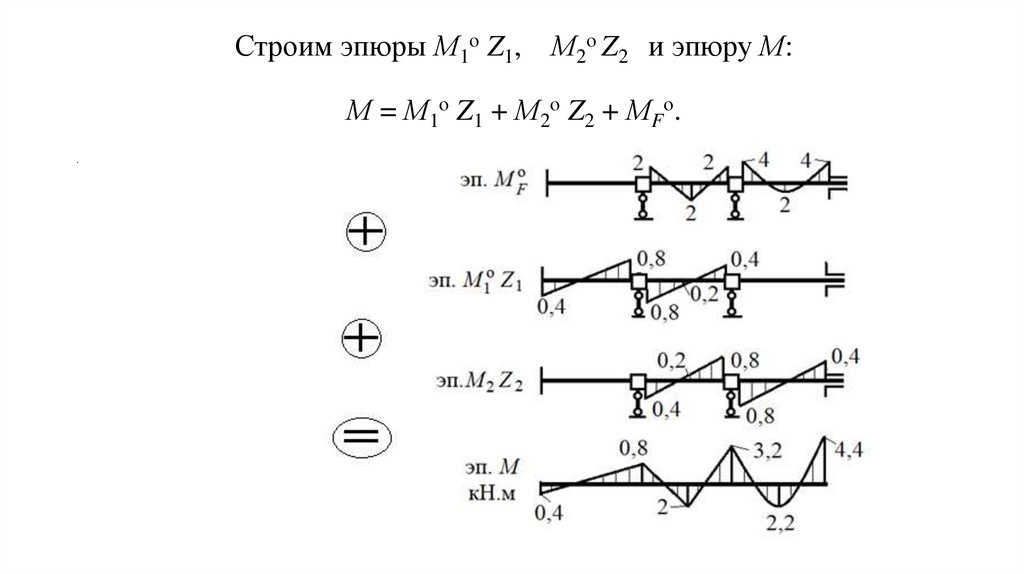
Строим эпюры М1о Z1,
М2о Z2 и эпюру М:
М = М1о Z1 + М2о Z2 + МFо.
.

7.

Строим эпюру Q по эпюре М.
Определяем опорные реакции по
эпюрам Q и М, вырезая узлы.
Делаем статическую проверку: ΣХ = 0;
ΣY = 1,7 + 8,3 + 6,3 – 0,3 – 4 – 3·4 = 0;
ΣМК = 4,4 + 0,4 – 0,3·10 +1,7·6 – 4·4 + 8,3·2 – 6,3·2 = 0.

8.

Пример 8.2.8. Построить эпюру изгибающих моментов М. EI = const.
Степень статической неопределимости: пст = 3К – Ш = 3∙3 – 5 = 4.
Степень кинематической неопределимости: nк =1+1 = 2.
Определим относительные жёсткости стержней рамы
и приведём их к единому множителю:
i = EI/8;
iриг. = 2EI/8 = 2i;

9.

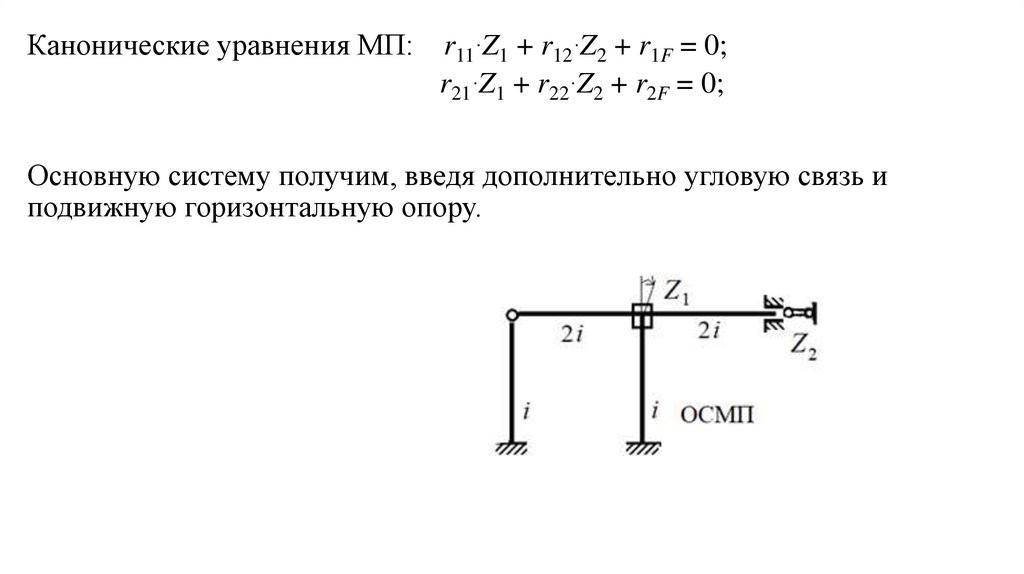
Канонические уравнения МП: r11∙Z1 + r12∙Z2 + r1F = 0;
r21∙Z1 + r22∙Z2 + r2F = 0;
Основную систему получим, введя дополнительно угловую связь и
подвижную горизонтальную опору.

10.

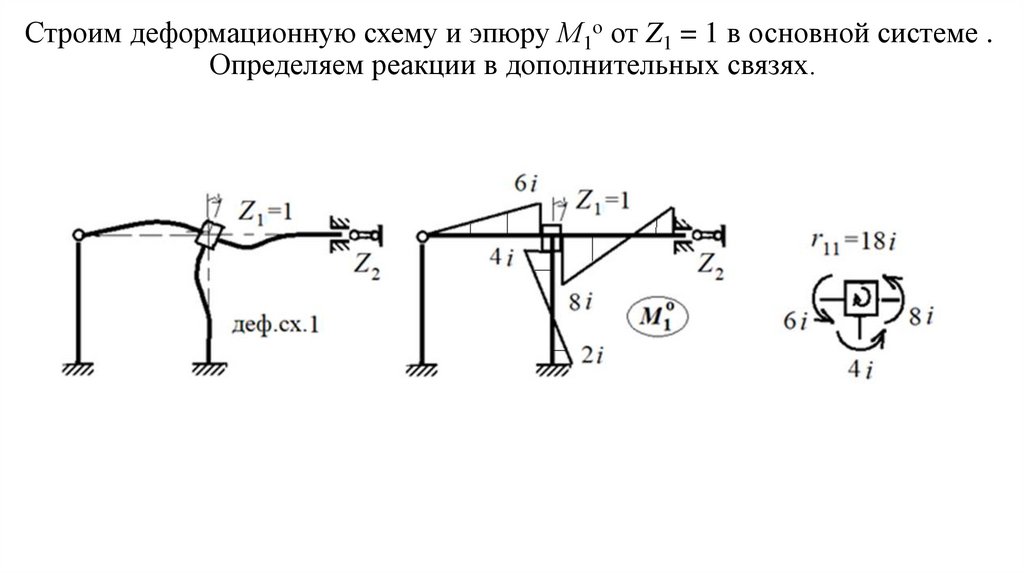
Строим деформационную схему и эпюру М1о от Z1 = 1 в основной системе .
Определяем реакции в дополнительных связях.

11.

Строим деформационную схему и эпюру М1о от Z1 = 1 в основной системе .
Определяем реакции в дополнительных связях.

12.

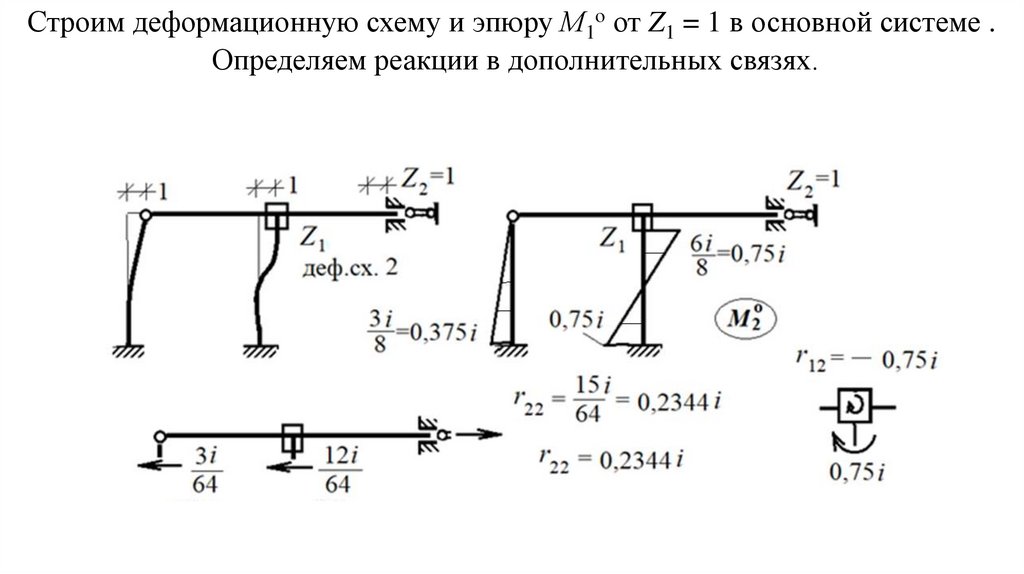
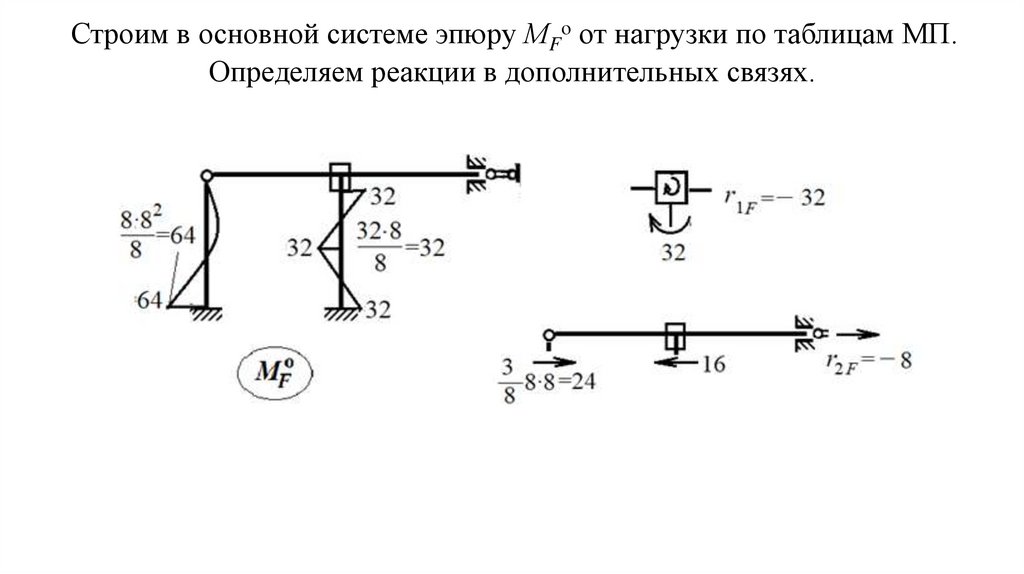
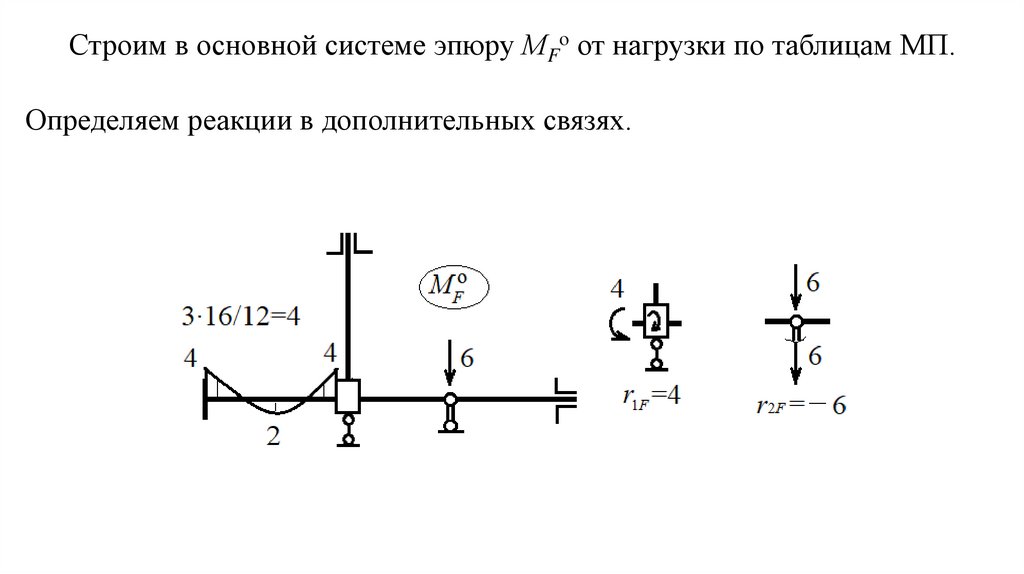
Строим в основной системе эпюру МFо от нагрузки по таблицам МП.
Определяем реакции в дополнительных связях.

13.

Решаем канонические уравнения:
18i∙Z1 – 0,75i∙Z2 – 32 = 0; делим на – 0,75
– 0,75i∙Z1 + 0,2344i∙Z2 – 8 = 0; делим на 0,2344
24i∙Z1 – i∙Z2 – 42,67 = 0;
–3,2i∙Z1 + i∙Z2 – 34,13 = 0;
20,8 i∙Z1
складываем…
– 76,8 = 0; → Z1 = 3,69/i;
Проверка: 18i∙3,69 – 0,75∙45,94 – 32 = 0,03.
Z2 = 45,94/i.

14.

Строим эпюры М1о∙Z1 , М2о∙Z2 и эпюру М: М = М1о∙Z1 + М2о∙Z2 + МFо:

15.

Строим эпюру поперечных сил Q по эпюре моментов М, а эпюру
продольных сил N по эпюре Q.

16.

Определяем реакции опор по эпюрам М, Q и N.
Делаем статическую проверку: ΣХ = 8∙8 – 32 – 42,15 + 10,15 = 0;
ΣМК = –81,23 + 4,92 +14,77 – 5,54·16 + (42,15–10,15)∙4 = 0;
ΣY = 5,54 – 2,77 –2,77 = 0.

17.

Определим экстремальное значение параболы в эпюре моментов:
q = dQ/dx; 8 = 42,15/x; х = 5,28 м.

18.

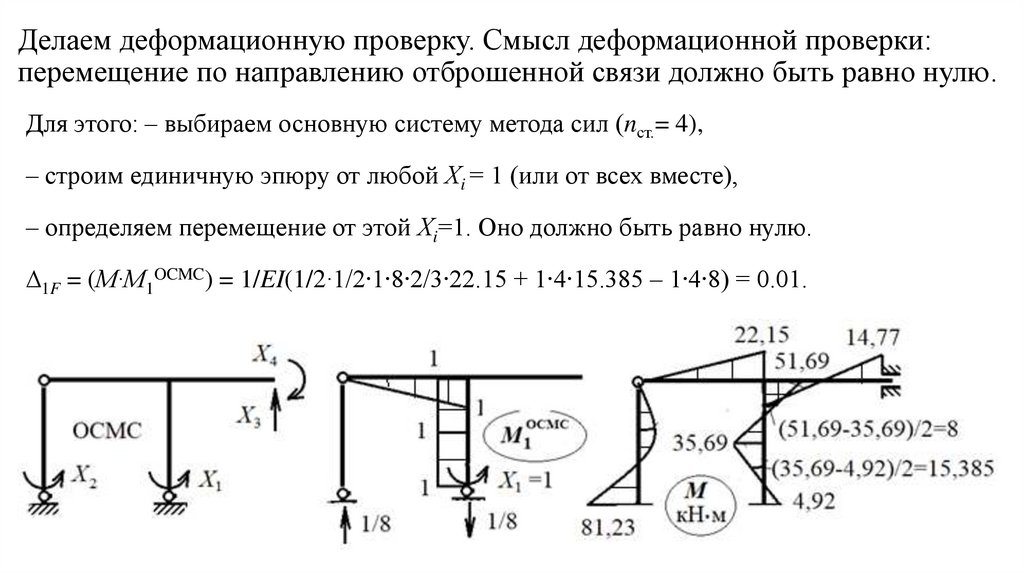
Делаем деформационную проверку. Смысл деформационной проверки:
перемещение по направлению отброшенной связи должно быть равно нулю.
Для этого: – выбираем основную систему метода сил (nст.= 4),
– строим единичную эпюру от любой Хi = 1 (или от всех вместе),
– определяем перемещение от этой Хi=1. Оно должно быть равно нулю.
∆1F = (М∙М1OCMC) = 1/EI(1/2∙1/2∙1∙8∙2/3∙22.15 + 1∙4∙15.385 – 1∙4∙8) = 0.01.

19.

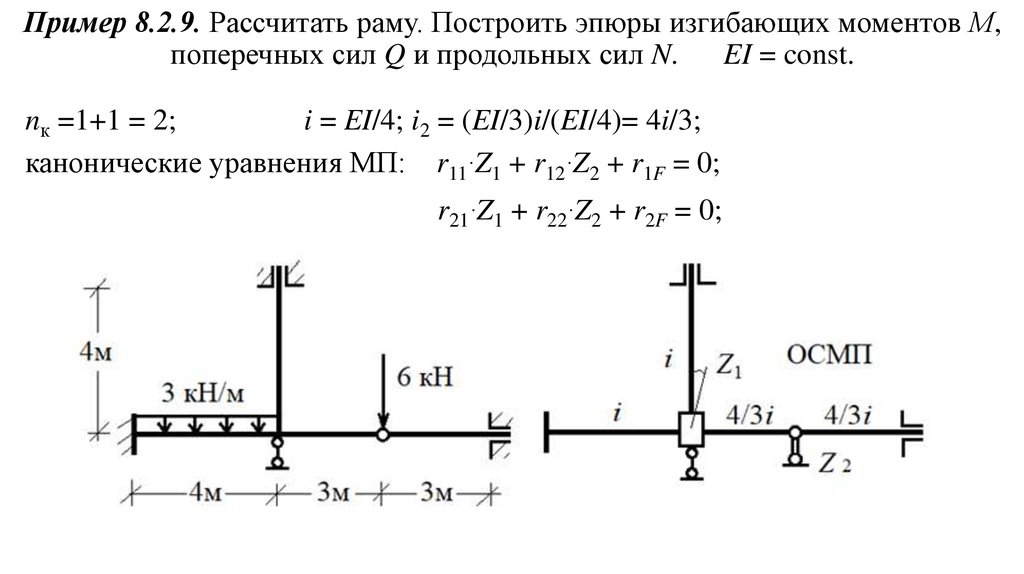
Пример 8.2.9. Рассчитать раму. Построить эпюры изгибающих моментов М,
поперечных сил Q и продольных сил N.
EI = const.
nк =1+1 = 2;
i = EI/4; i2 = (EI/3)i/(EI/4)= 4i/3;
канонические уравнения МП: r11∙Z1 + r12∙Z2 + r1F = 0;
r21∙Z1 + r22∙Z2 + r2F = 0;

20.

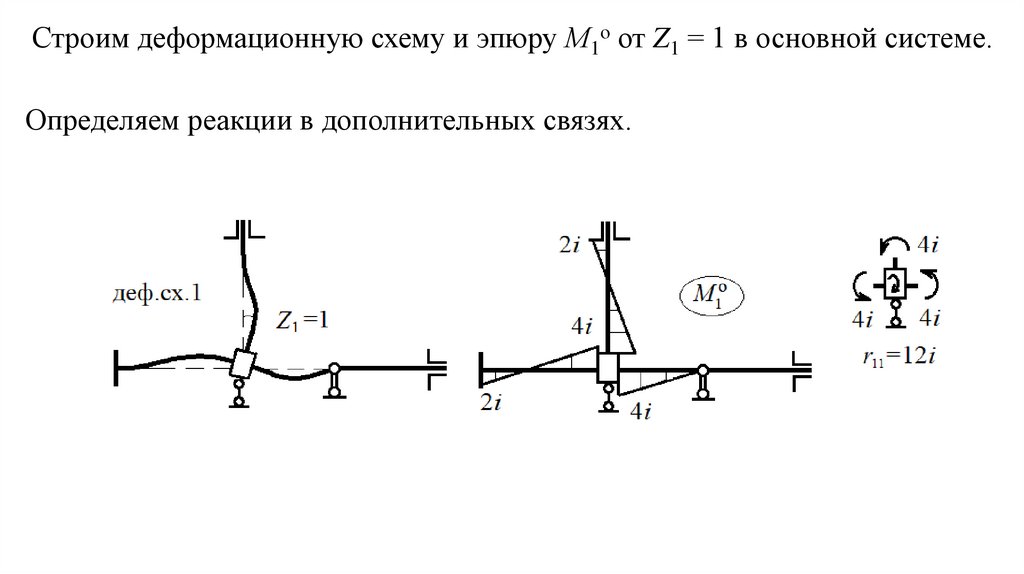
Строим деформационную схему и эпюру М1о от Z1 = 1 в основной системе.
Определяем реакции в дополнительных связях.

21.

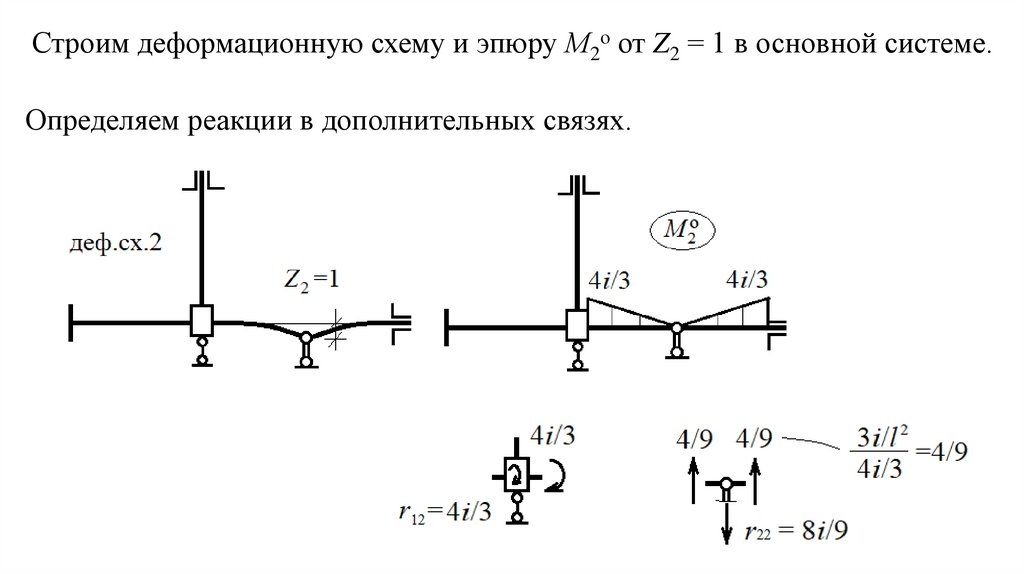
Строим деформационную схему и эпюру М2о от Z2 = 1 в основной системе.
Определяем реакции в дополнительных связях.

22.

Строим в основной системе эпюру МFо от нагрузки по таблицам МП.
Определяем реакции в дополнительных связях.

23.

Решаем канонические уравнения:
12i∙Z1 – 4i/3∙Z2 + 4 = 0;
– 4i/3∙Z1 + 8i/9∙Z2 – 6 = 0;
Z1 = 0,5/i;
Z2 = 7,5/i.
Проверка: 12∙0,5 – 4/3∙7,5 + 4 = 0,.

24.

Строим эпюры М1о∙Z1 , М2о∙Z2 и эпюру М: М = М1о∙Z1 + М2о∙Z2 + МFо:
Проверяем равновесие узла.

25.

Строим эпюру поперечных сил Q по эпюре моментов М,
а эпюру продольных сил N по эпюре Q.

26.

Определяем реакции опор по эпюрам.
Делаем статическую проверку: ΣХ = 0,75 – 0,75 = 0;
ΣY = 5,25 + 9,42 + 3,33 – 3∙4 – 6 = 0;
ΣМК = 1 – 0,75∙4 – 3 + 5,25∙4 – 3∙4∙2 + 6∙3 – 3,33∙6 +10 = 0.

27.

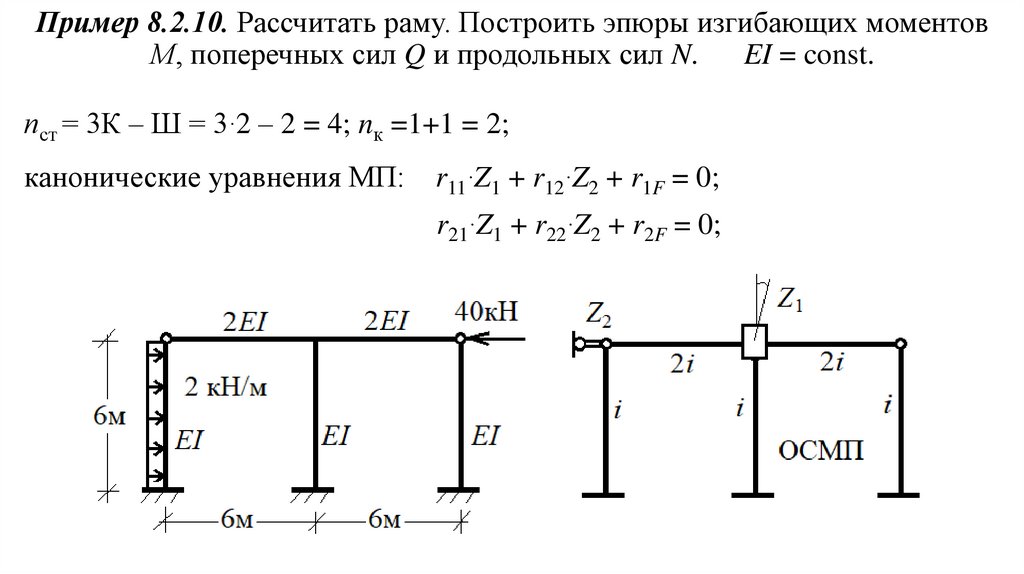
Пример 8.2.10. Рассчитать раму. Построить эпюры изгибающих моментов
М, поперечных сил Q и продольных сил N.
EI = const.
пст = 3К – Ш = 3∙2 – 2 = 4; nк =1+1 = 2;
канонические уравнения МП:
r11∙Z1 + r12∙Z2 + r1F = 0;
r21∙Z1 + r22∙Z2 + r2F = 0;

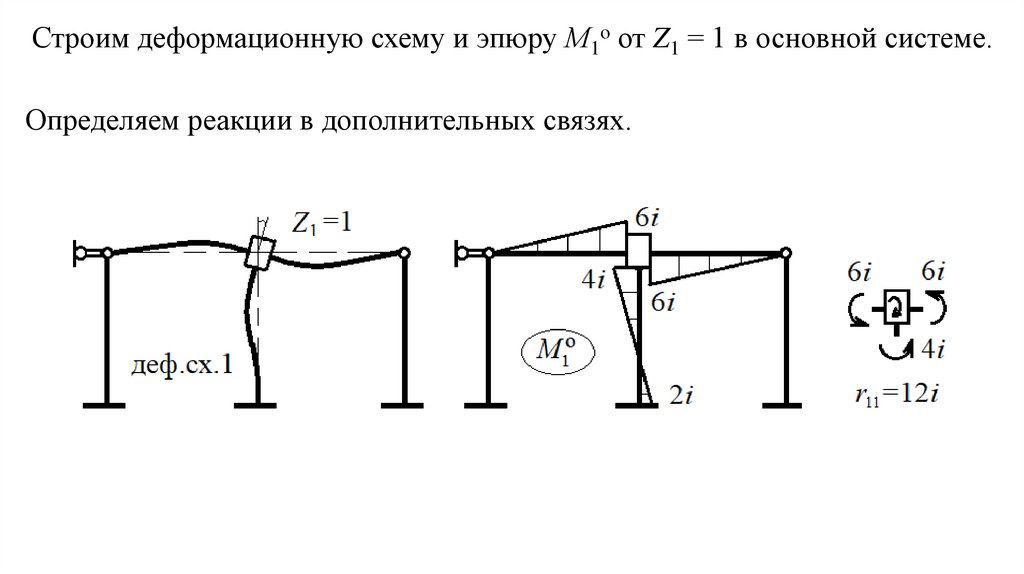
28.

Строим деформационную схему и эпюру М1о от Z1 = 1 в основной системе.
Определяем реакции в дополнительных связях.

29.

Строим деформационную схему и эпюру М2о от Z2 = 1 в основной системе.
Определяем реакции в дополнительных связях.

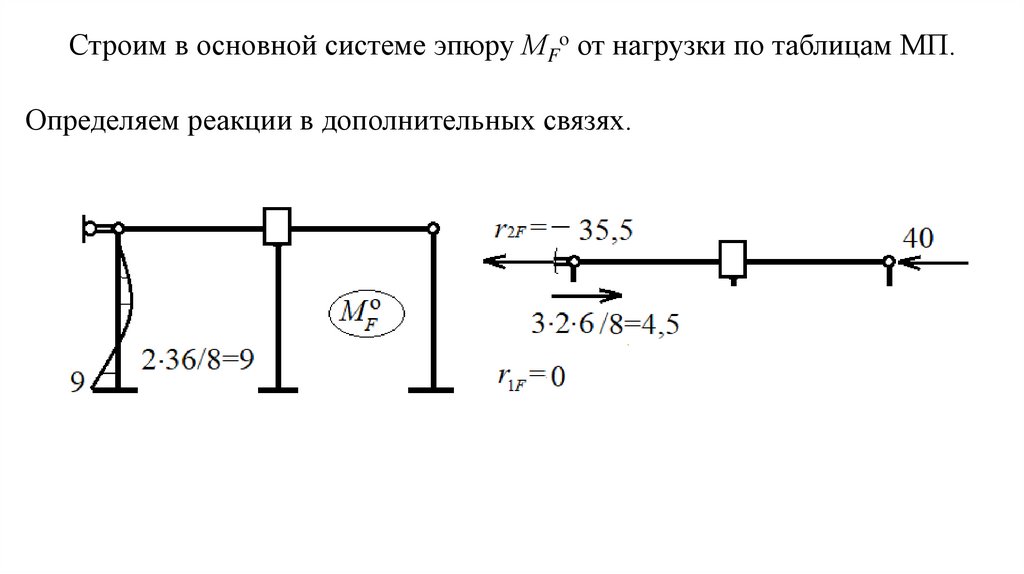
30.

Строим в основной системе эпюру МFо от нагрузки по таблицам МП.
Определяем реакции в дополнительных связях.

31.

Решаем канонические уравнения:
16i∙Z1 + 1i∙Z2 = 0;
1i∙Z1 + 0,5i∙Z2 – 35,5 = 0;
Z1 = – 5,07/i;
Z2 = 81,14/i.
Проверка: –1i∙5,07/i + 0,5i∙81,14/i – 35,5 = 0.

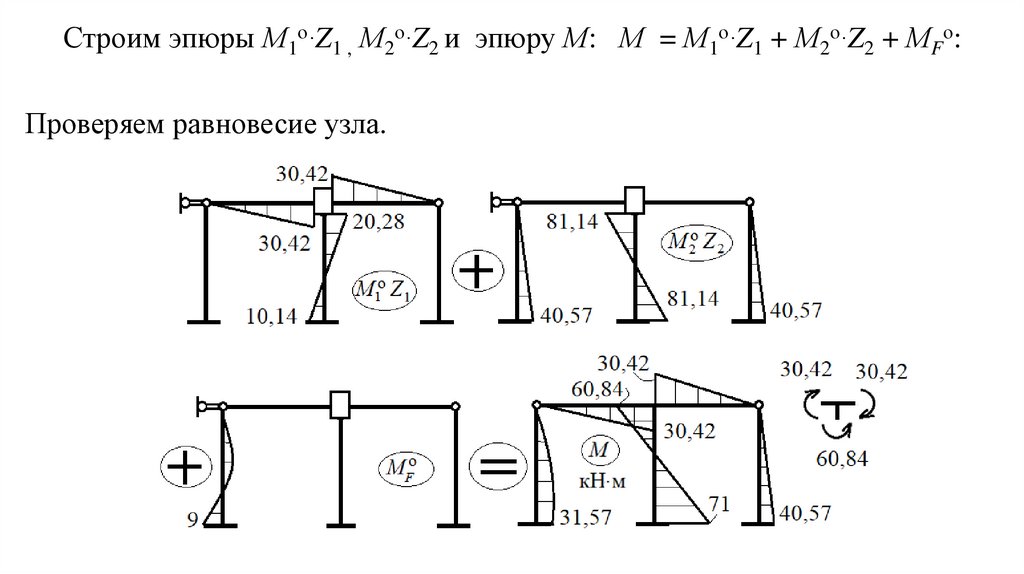
32.

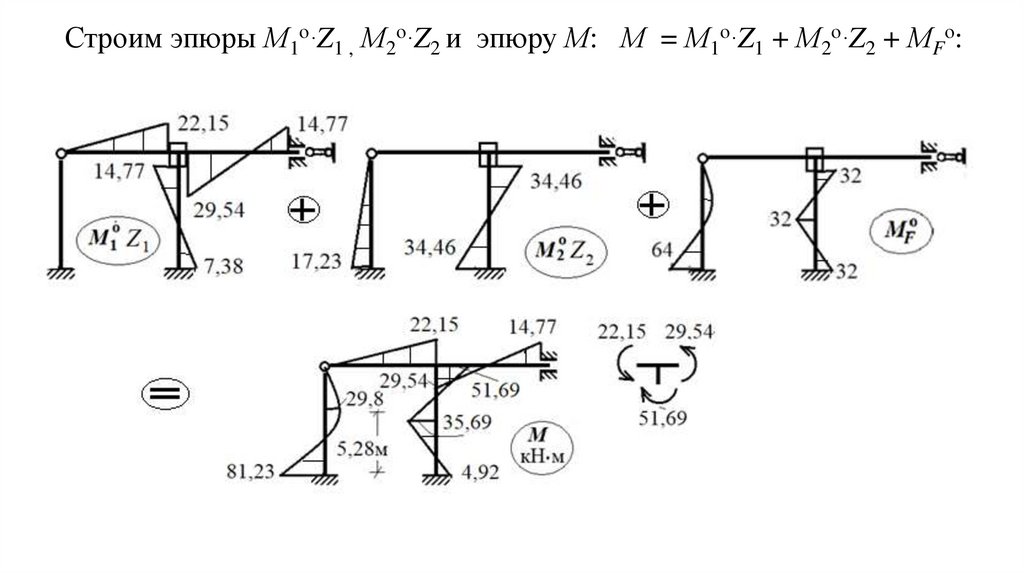
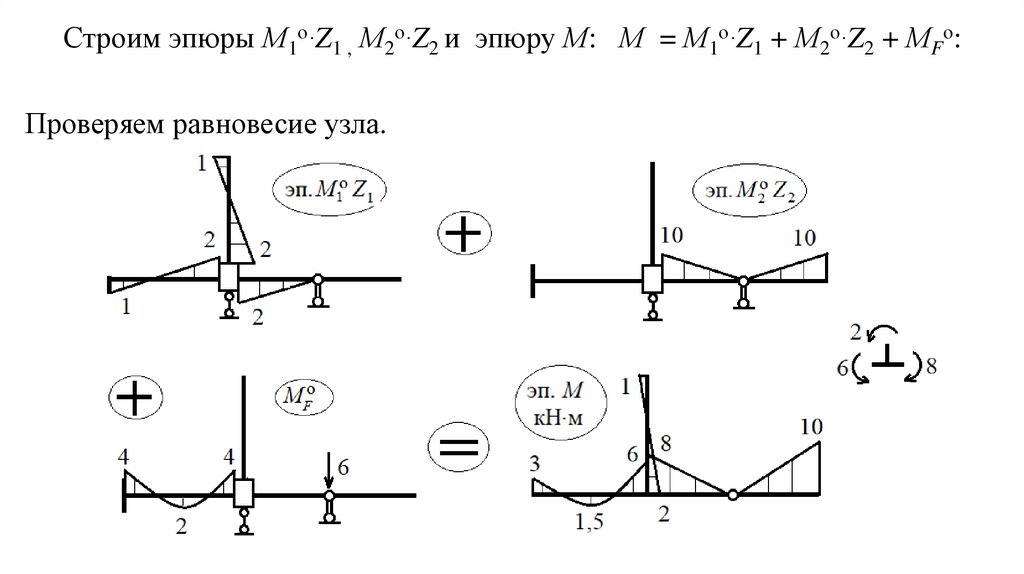
Строим эпюры М1о∙Z1 , М2о∙Z2 и эпюру М: М = М1о∙Z1 + М2о∙Z2 + МFо:
Проверяем равновесие узла.

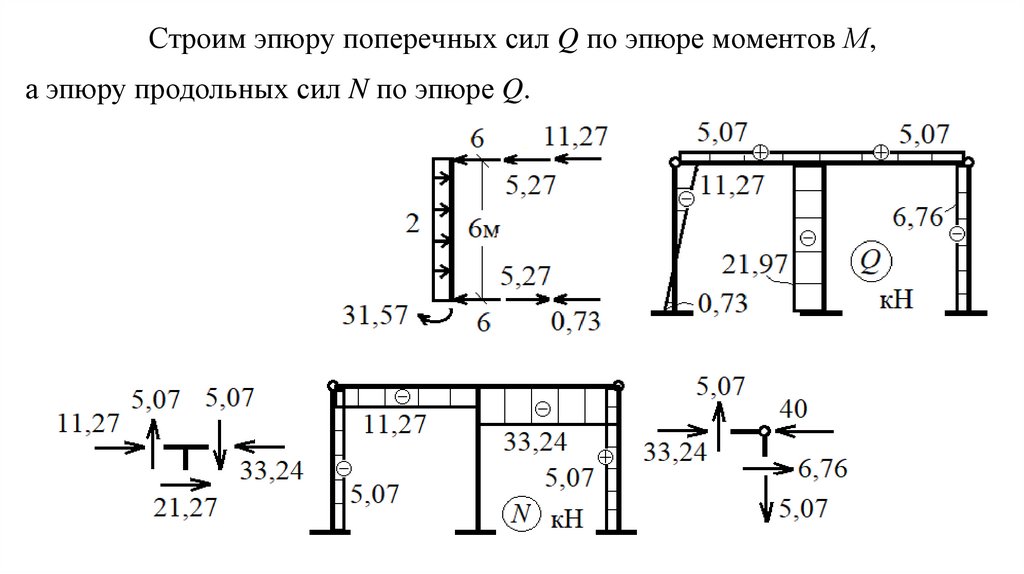
33.

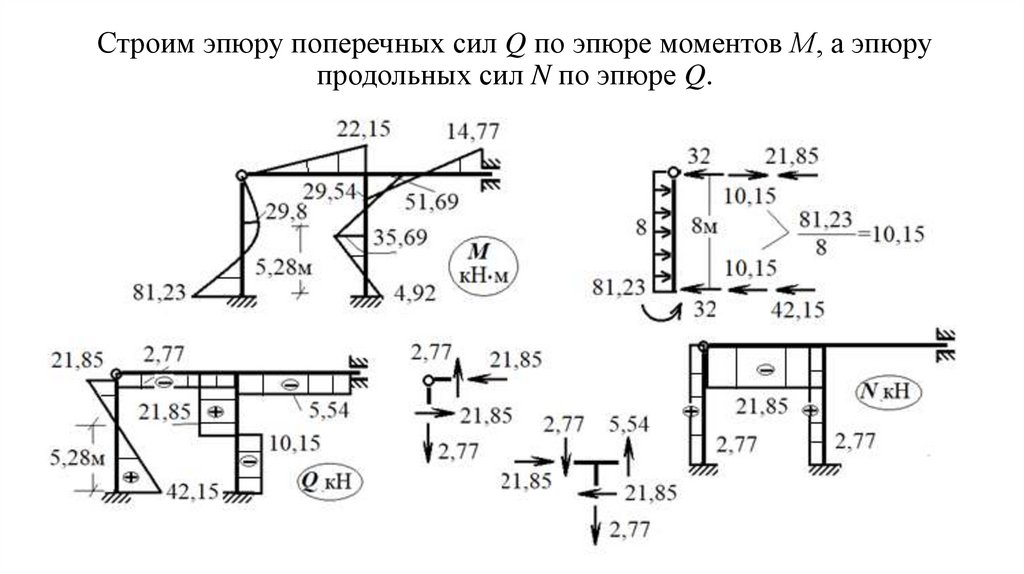
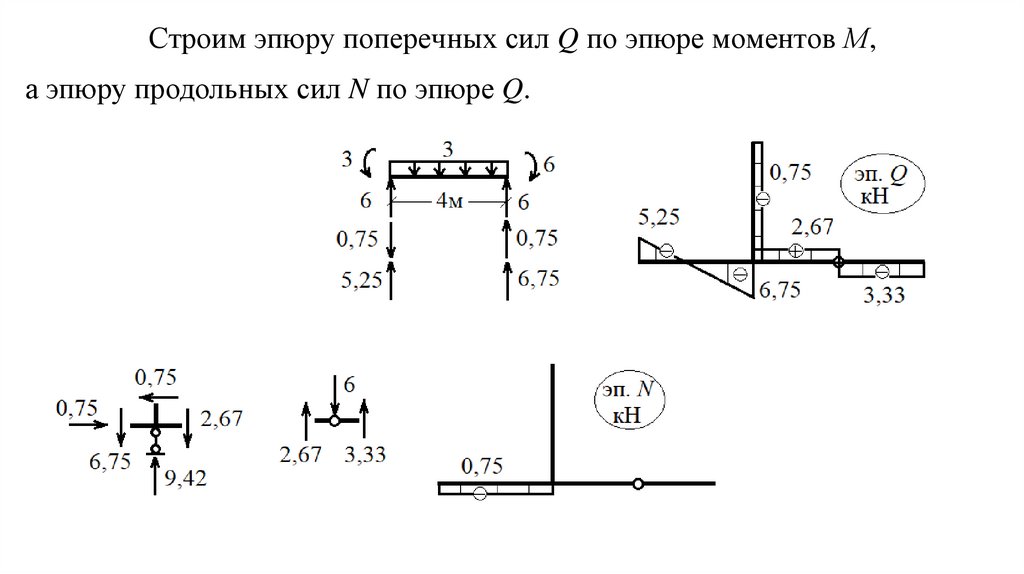
Строим эпюру поперечных сил Q по эпюре моментов М,
а эпюру продольных сил N по эпюре Q.

34.

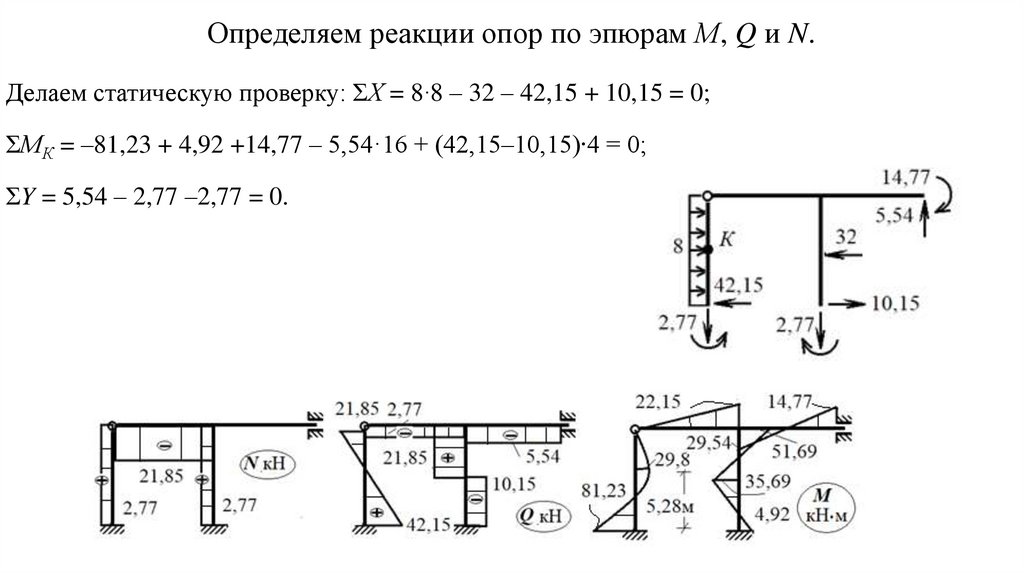
Определяем реакции опор по эпюрам.
Делаем статическую проверку: ΣХ = …= 0;
ΣY = …= 0;
ΣМК = … = 0.

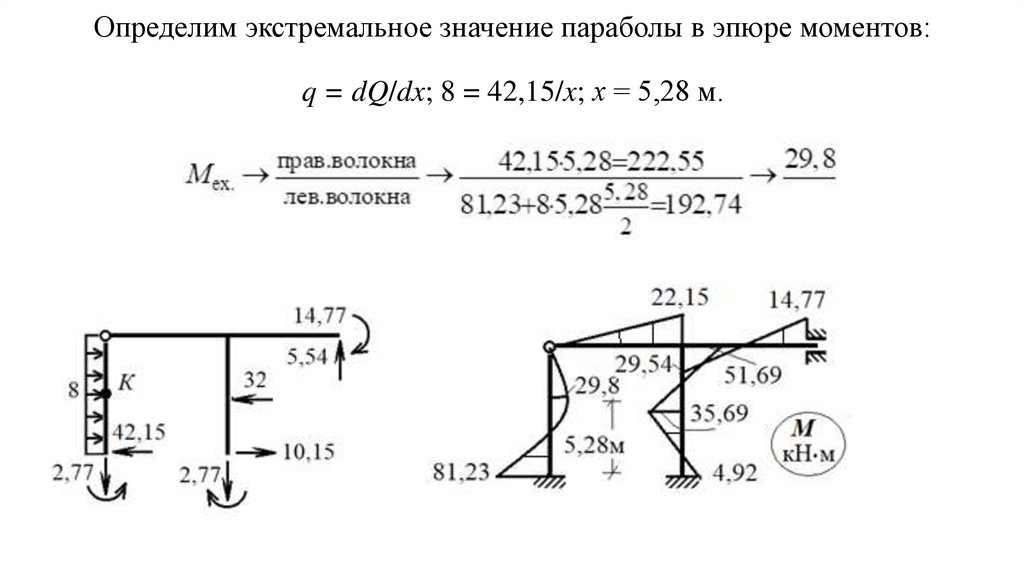
35.

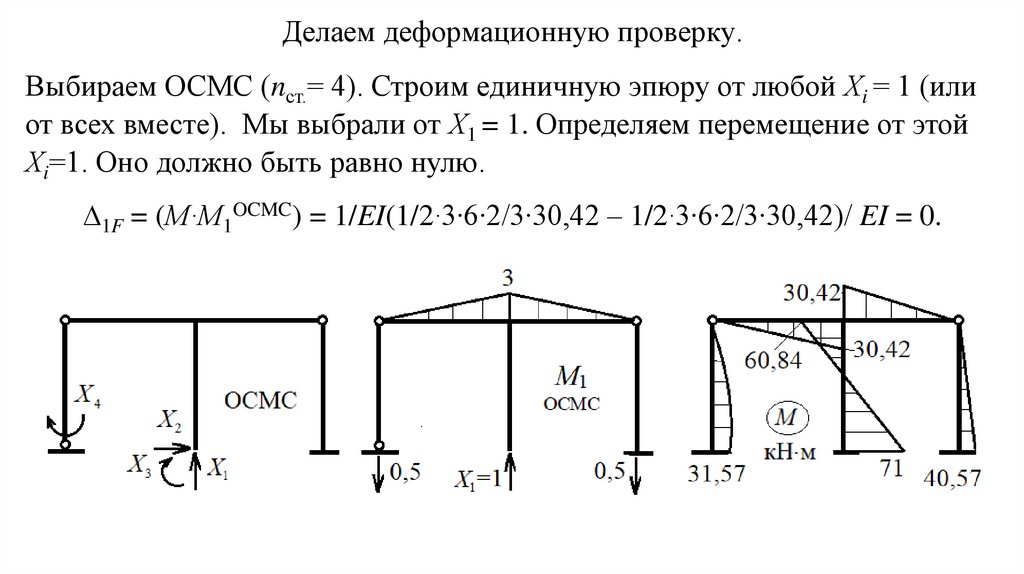
Делаем деформационную проверку.
Выбираем ОСМС (nст.= 4). Строим единичную эпюру от любой Хi = 1 (или
от всех вместе). Мы выбрали от Х1 = 1. Определяем перемещение от этой
Хi=1. Оно должно быть равно нулю.
∆1F = (М∙М1OCMC) = 1/EI(1/2∙3∙6∙2/3∙30,42 – 1/2∙3∙6∙2/3∙30,42)/ EI = 0.

36.

Пример 8.2.11. Рассчитать раму. Построить М, Q и N.
nк =1+1 = 2. i = EI/6; левый ригель: iриг. = (4EI/3)/8 = 2i.
r11∙Z1 + r12∙Z2 + r1F = 0;
r21∙Z1 + r22∙Z2 + r2F = 0.

37.

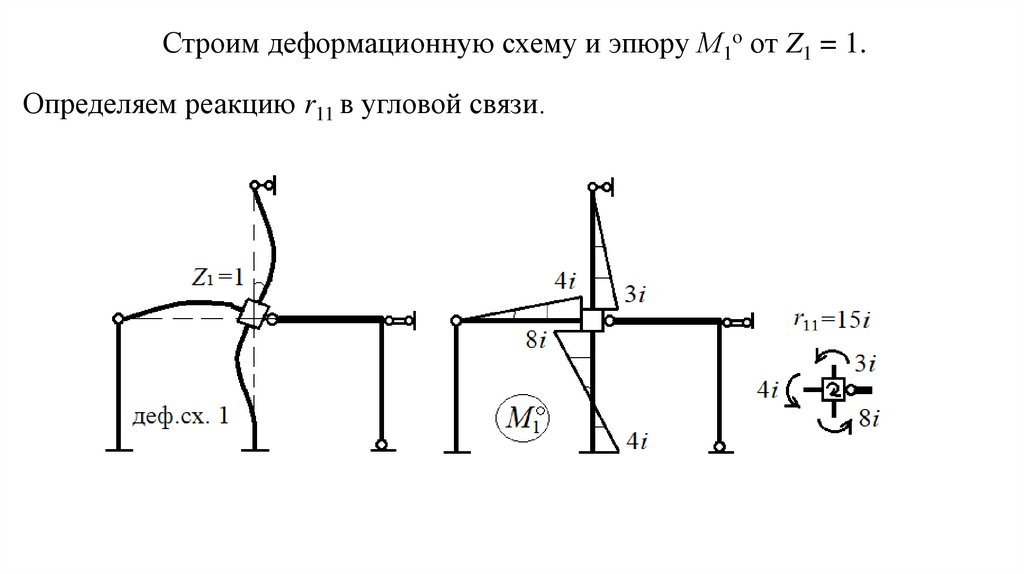
Строим деформационную схему и эпюру М1о от Z1 = 1.
Определяем реакцию r11 в угловой связи.

38.

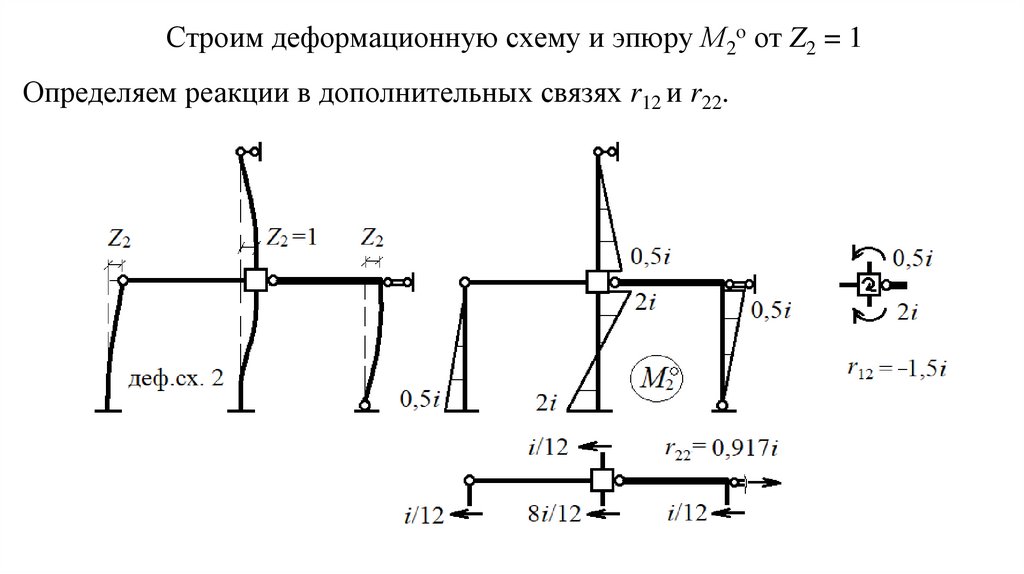
Строим деформационную схему и эпюру М2о от Z2 = 1
Определяем реакции в дополнительных связях r12 и r22.

39.

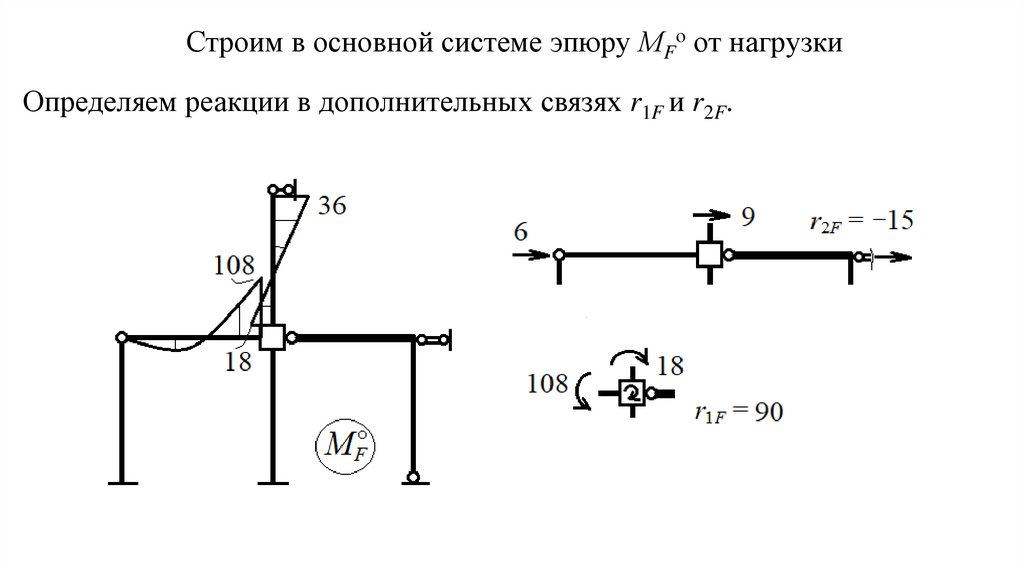
Строим в основной системе эпюру МFо от нагрузки
Определяем реакции в дополнительных связях r1F и r2F.

40.

Решаем канонические уравнения
15i∙Z1 – 1,5i∙Z2 + 90 = 0; делим на 1,5,
– 1,5i∙Z1 + 0,917i∙Z2 – 15 = 0; делим на 0,917,
10i∙Z1 – i∙Z2 + 60 = 0;
–1,636i∙Z1 + i∙Z2 – 16,358 = 0;
8,364 i∙Z1
складываем:
+ 43,64 = 0;
Z1 = – 5,22/i; Z2 = 7,83/i.
Проверка: 18∙(– 5,22) – 1,5∙7,83 + 90 = 0,05.
% ошибки: 0,05∙100%/90 = 0,06% < 1%.

41.

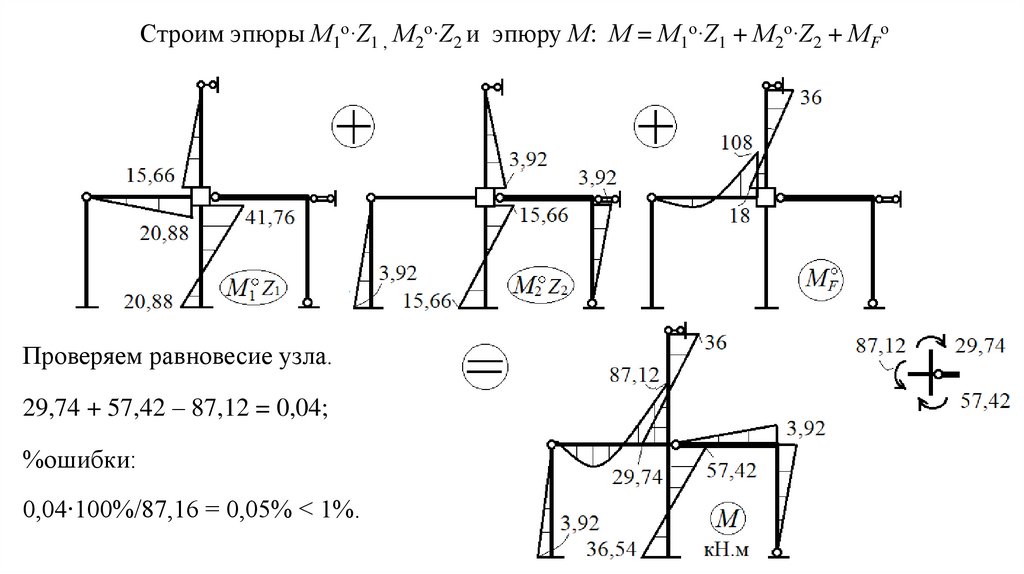
Строим эпюры М1о∙Z1 , М2о∙Z2 и эпюру М: М = М1о∙Z1 + М2о∙Z2 + МFо
Проверяем равновесие узла.
29,74 + 57,42 – 87,12 = 0,04;
%ошибки:
0,04∙100%/87,16 = 0,05% < 1%.

42.

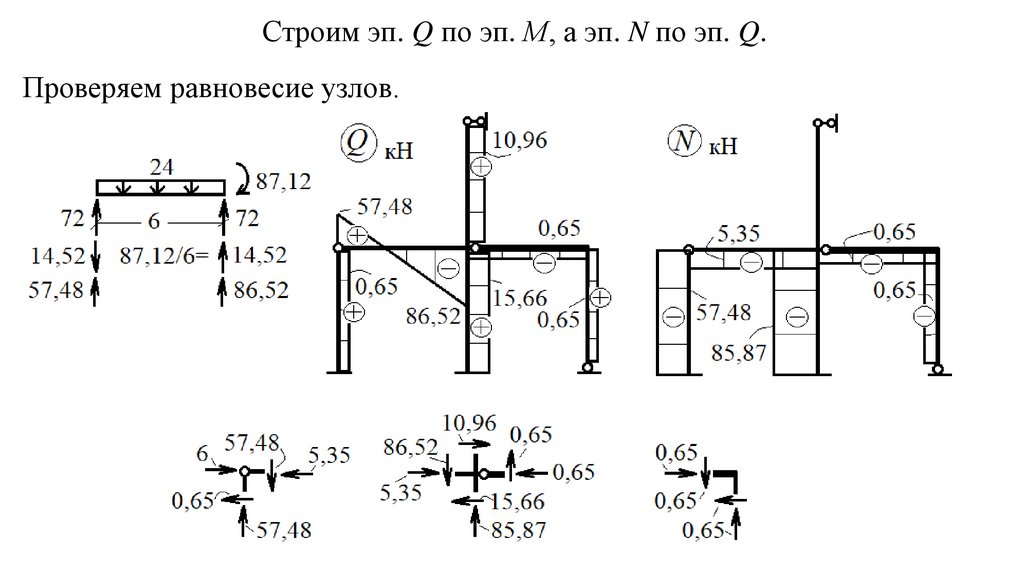
Строим эп. Q по эп. М, а эп. N по эп. Q.
Проверяем равновесие узлов.

43.

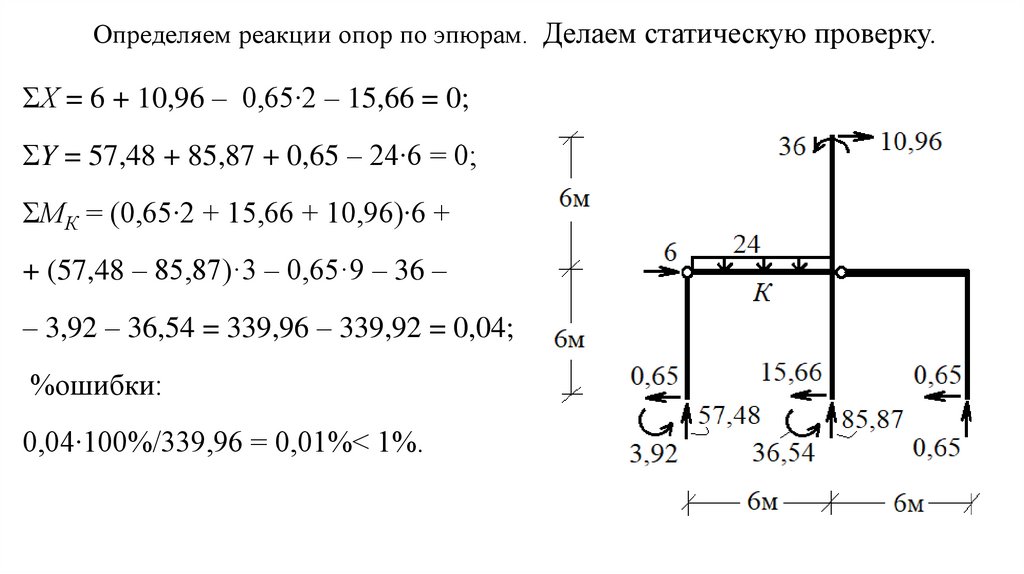
Определяем реакции опор по эпюрам. Делаем статическую проверку.
ΣХ = 6 + 10,96 – 0,65∙2 – 15,66 = 0;
ΣY = 57,48 + 85,87 + 0,65 – 24∙6 = 0;
ΣМК = (0,65∙2 + 15,66 + 10,96)∙6 +
+ (57,48 – 85,87)·3 – 0,65·9 – 36 –
– 3,92 – 36,54 = 339,96 – 339,92 = 0,04;
%ошибки:
0,04∙100%/339,96 = 0,01%< 1%.

44.

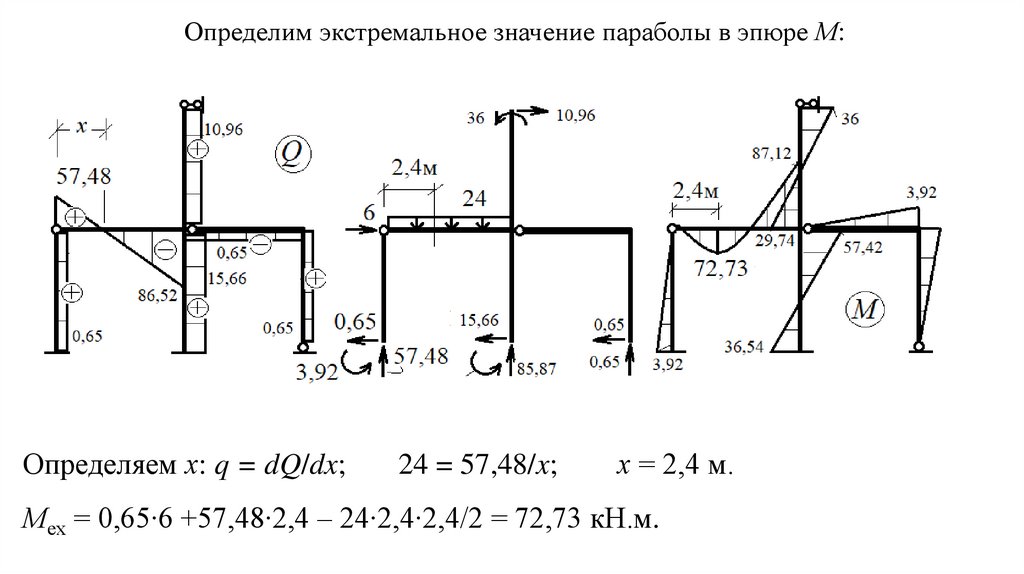
Определим экстремальное значение параболы в эпюре М:
Определяем х: q = dQ/dx;
24 = 57,48/x;
х = 2,4 м.
Мех = 0,65∙6 +57,48∙2,4 – 24∙2,4∙2,4/2 = 72,73 кН.м.

45.

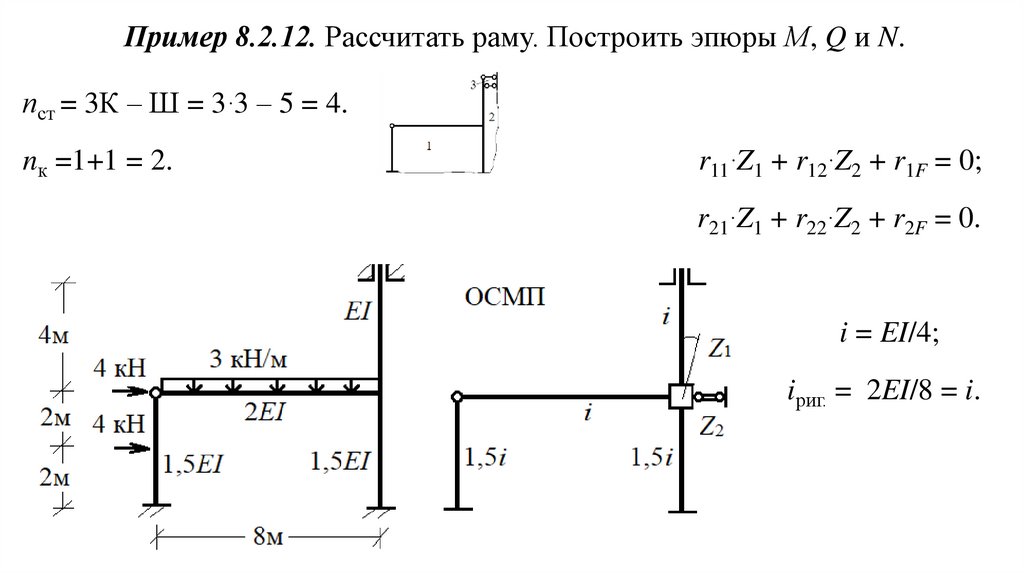
Пример 8.2.12. Рассчитать раму. Построить эпюры М, Q и N.
пст = 3К – Ш = 3∙3 – 5 = 4.
nк =1+1 = 2.
r11∙Z1 + r12∙Z2 + r1F = 0;
r21∙Z1 + r22∙Z2 + r2F = 0.
i = EI/4;
iриг. = 2EI/8 = i.

46.

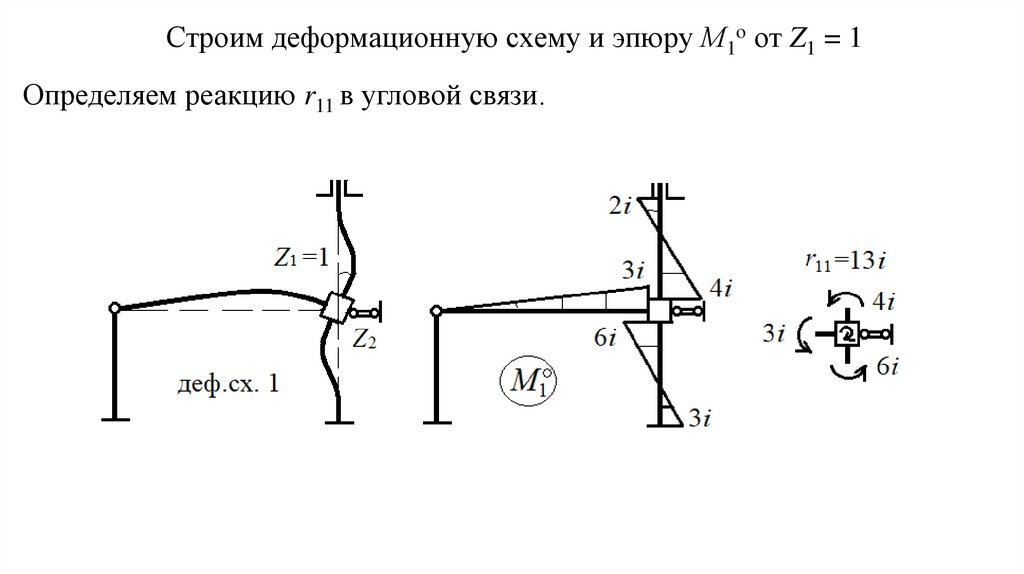
Строим деформационную схему и эпюру М1о от Z1 = 1
Определяем реакцию r11 в угловой связи.

47.

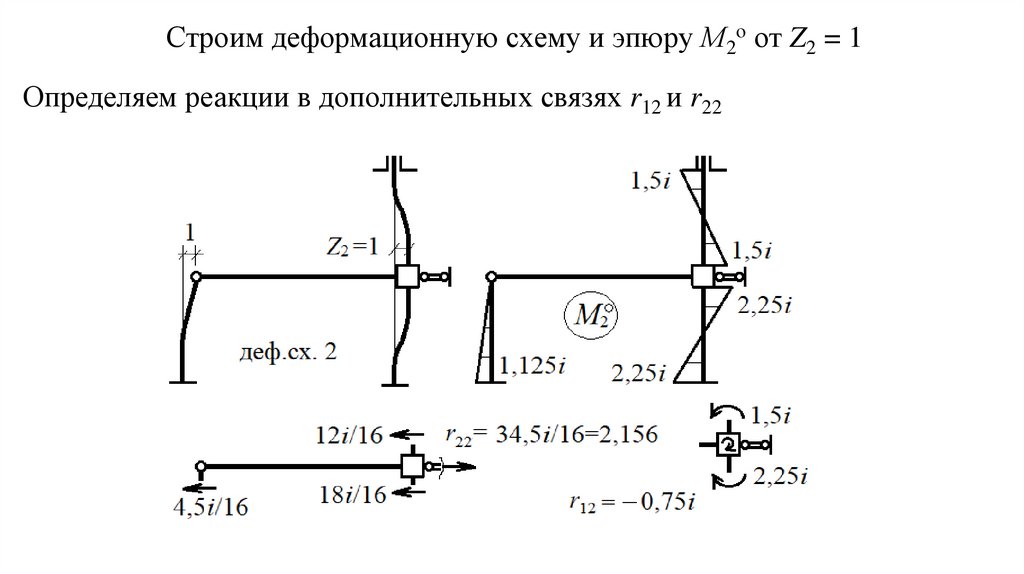
Строим деформационную схему и эпюру М2о от Z2 = 1
Определяем реакции в дополнительных связях r12 и r22

48.

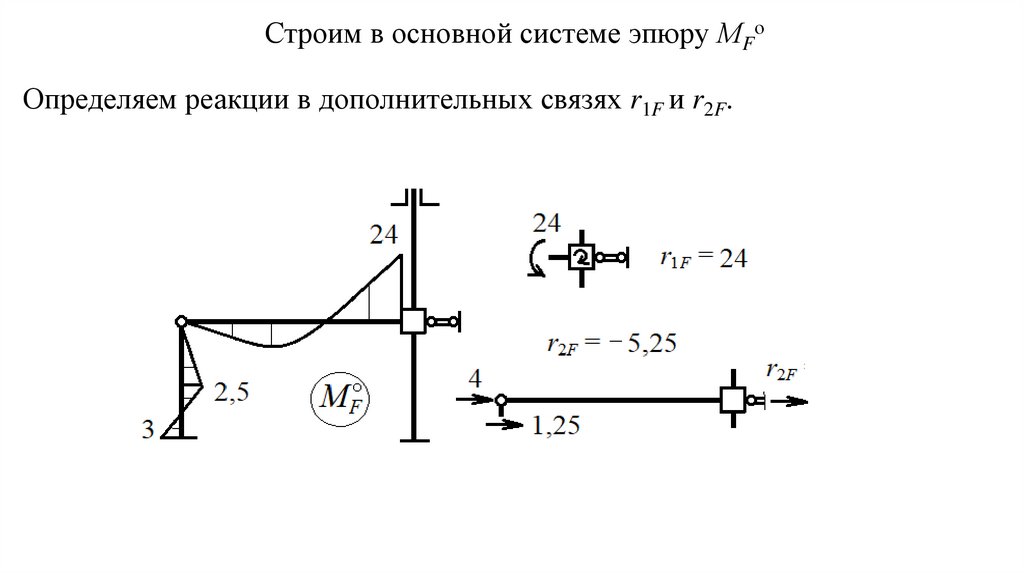
Строим в основной системе эпюру МFо
Определяем реакции в дополнительных связях r1F и r2F.

49.

Решаем канонические уравнения:
13i∙Z1 – 0,75i∙Z2 + 24 = 0; делим на 0,75,
– 0,75i∙Z1 + 2,156i∙Z2 – 15 = 0; делим на 2,156,
17,33i∙Z1 – i∙Z2 + 32 = 0;
– 0,35i∙Z1 + i∙Z2 – 2,43 = 0;
16,99 i∙Z1
+ 30 = 0;
Z1 = – 1,74/i;
Проверка: 13∙(– 1,74) – 0,75∙1,83 + 24 = 0.
Z2 = 1,83/i.

50.

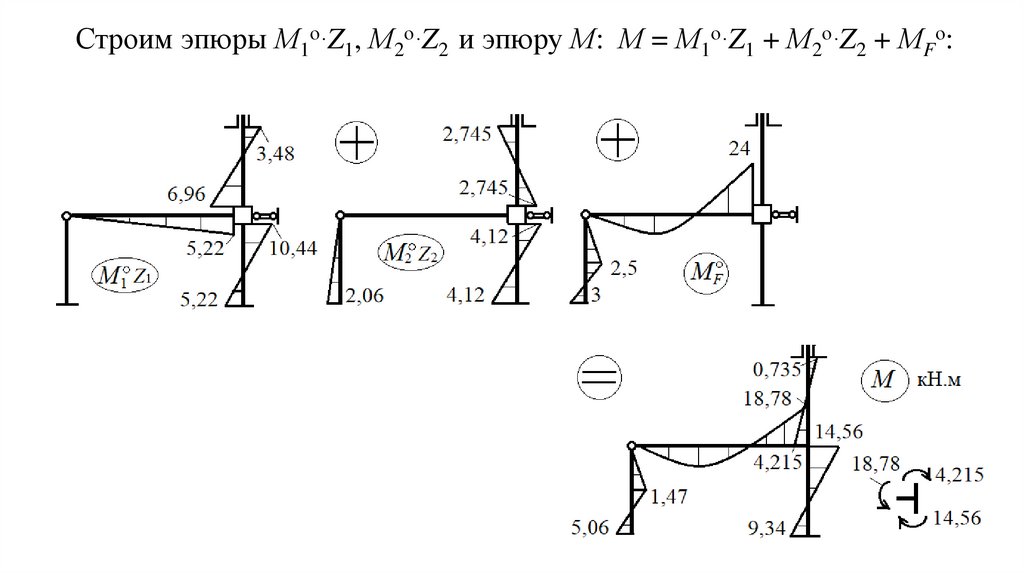
Строим эпюры М1о∙Z1, М2о∙Z2 и эпюру М: М = М1о∙Z1 + М2о∙Z2 + МFо:

51.

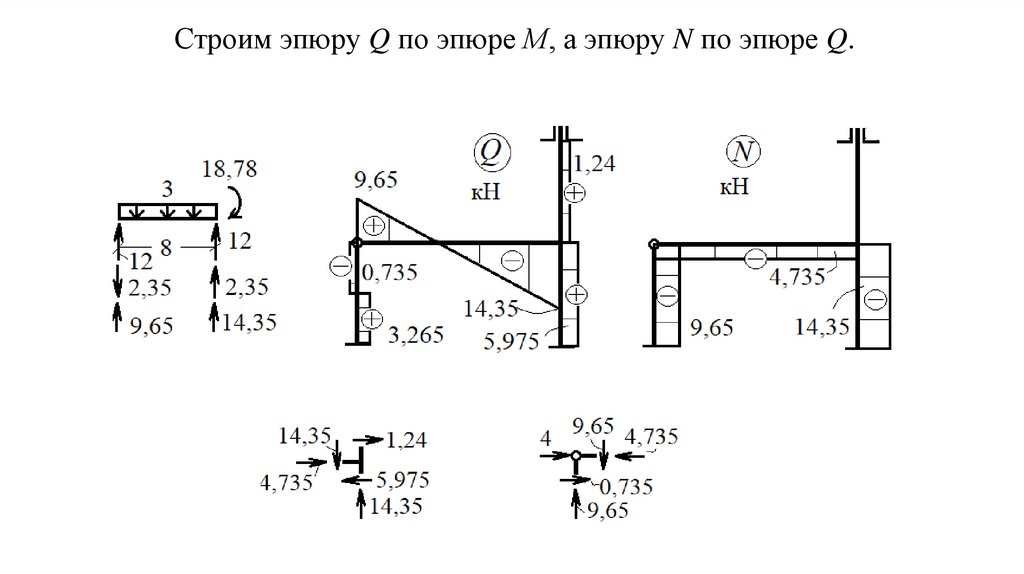
Строим эпюру Q по эпюре М, а эпюру N по эпюре Q.

52.

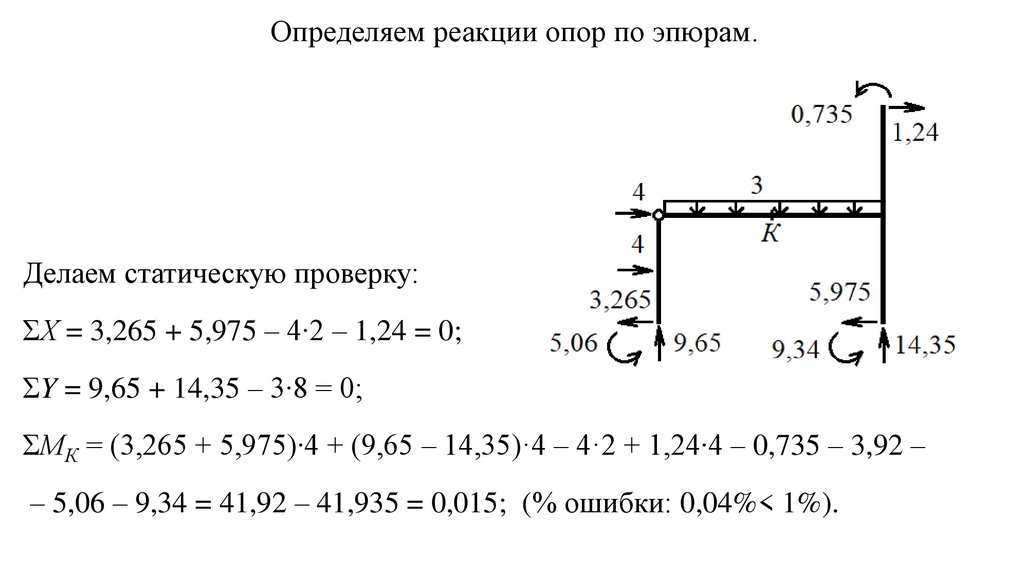
Определяем реакции опор по эпюрам.
Делаем статическую проверку:
ΣХ = 3,265 + 5,975 – 4∙2 – 1,24 = 0;
ΣY = 9,65 + 14,35 – 3∙8 = 0;
ΣМК = (3,265 + 5,975)∙4 + (9,65 – 14,35)·4 – 4·2 + 1,24∙4 – 0,735 – 3,92 –
– 5,06 – 9,34 = 41,92 – 41,935 = 0,015; (% ошибки: 0,04%< 1%).

53.

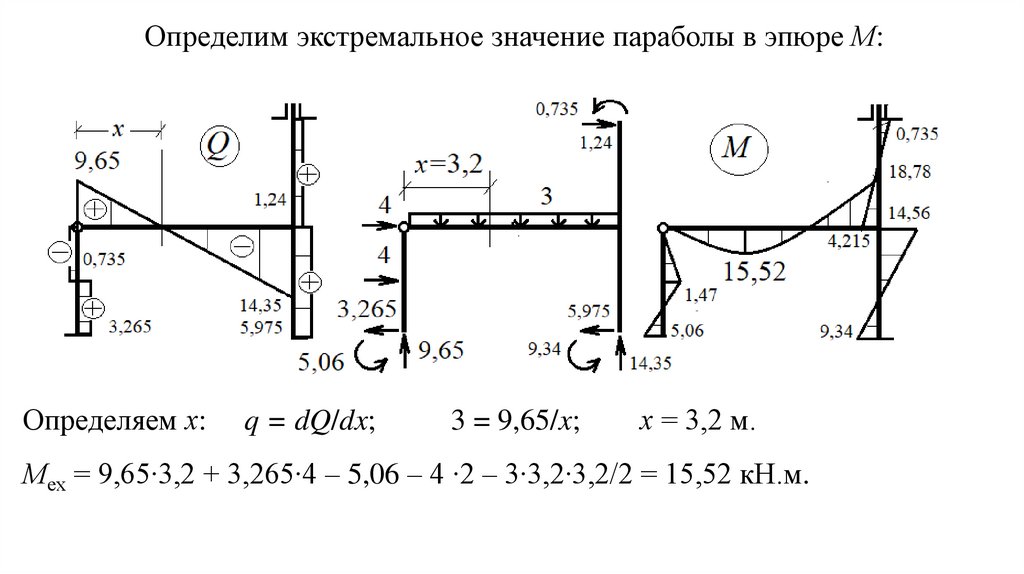
Определим экстремальное значение параболы в эпюре М:
Определяем х:
q = dQ/dx;
3 = 9,65/x;
х = 3,2 м.
Мех = 9,65∙3,2 + 3,265∙4 – 5,06 – 4 ∙2 – 3∙3,2∙3,2/2 = 15,52 кН.м.

54.

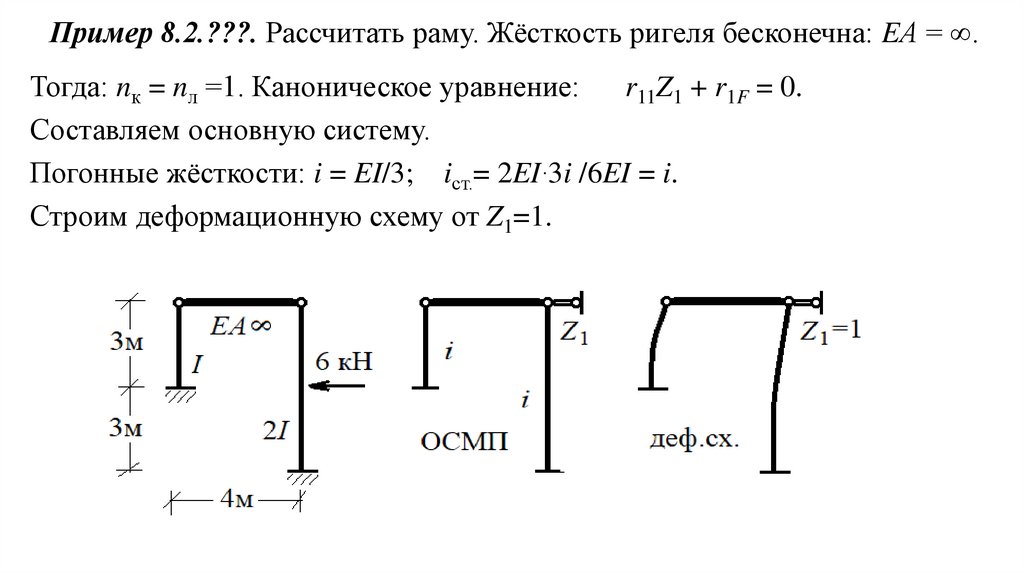
Пример 8.2.???. Рассчитать раму. Жёсткость ригеля бесконечна: EА = ∞.
Тогда: nк = nл =1. Каноническое уравнение:
r11Z1 + r1F = 0.
Составляем основную систему.
Погонные жёсткости: i = EI/3; iст.= 2EI∙3i /6EI = i.
Строим деформационную схему от Z1=1.

55.

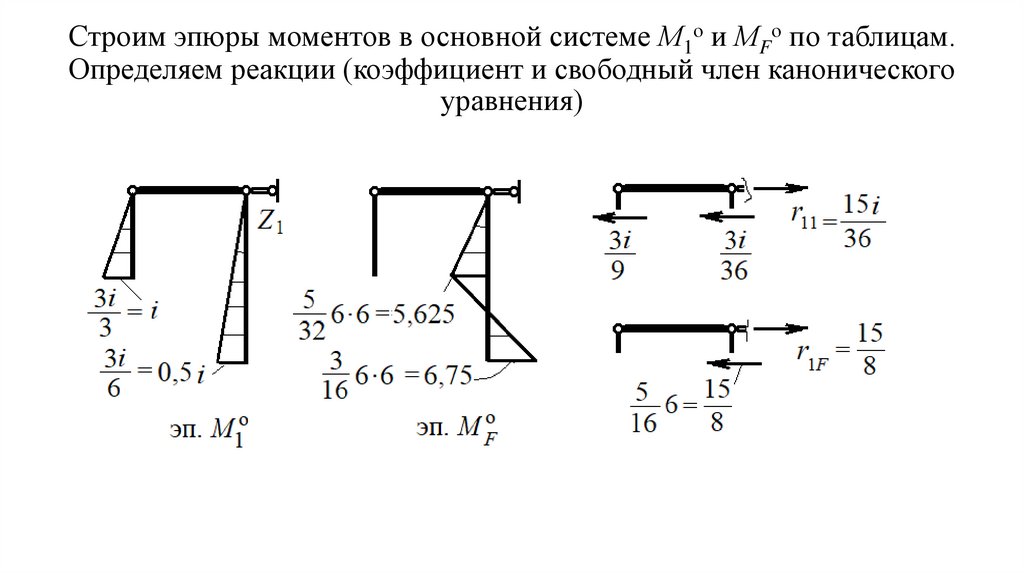
Строим эпюры моментов в основной системе М1о и МFо по таблицам.
Определяем реакции (коэффициент и свободный член канонического
уравнения)

56.

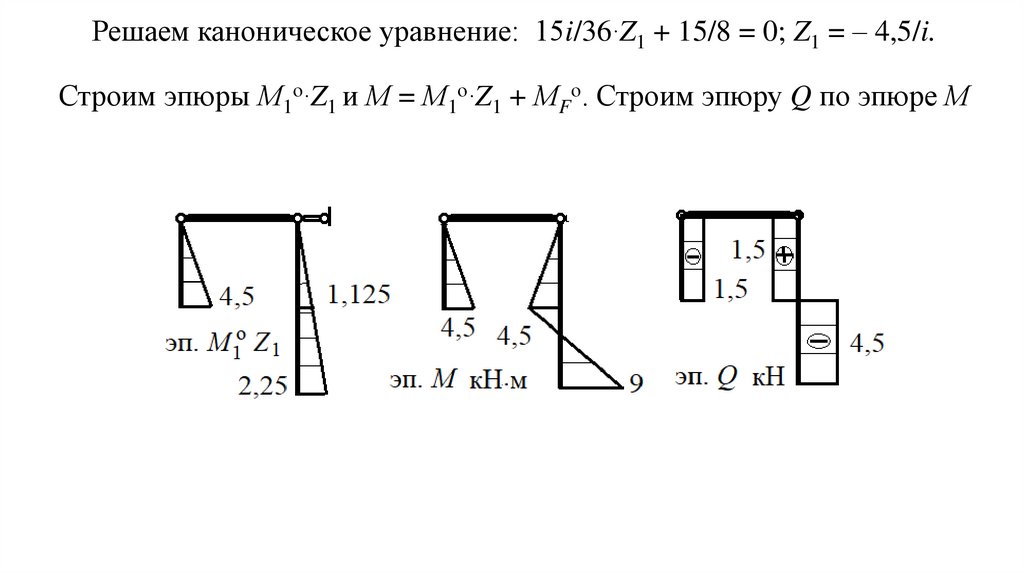
Решаем каноническое уравнение: 15i/36∙Z1 + 15/8 = 0; Z1 = – 4,5/i.
Строим эпюры М1о∙Z1 и М = М1о∙Z1 + МFо. Строим эпюру Q по эпюре М

57.

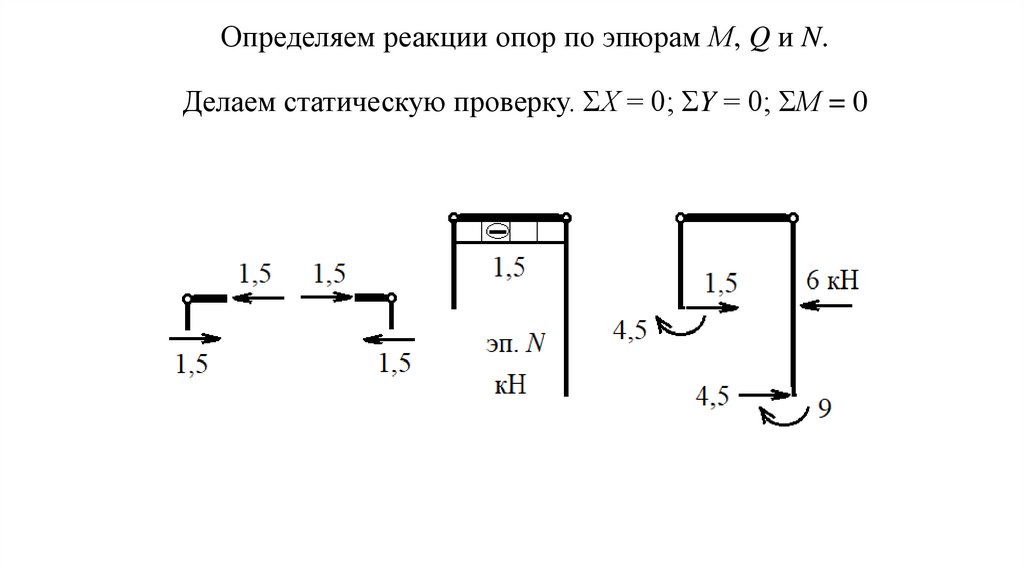
Определяем реакции опор по эпюрам М, Q и N.
Делаем статическую проверку. ΣХ = 0; ΣY = 0; ΣМ = 0

58.

Контрольные вопросы
1. Каков порядок расчёта балок и рам методом перемещений.
2. Как строятся эпюры моментов при расчёте балок и рам методом
перемещений?
3. Как проверить правильность расчёта балок и рам, выполненный методом
перемещений?
4. В чём заключается идея расчёта статически неопределимых систем
методом перемещений?

59.

Санкт-Петербургский государственный
архитектурно-строительный университет
кафедра Строительной механики
Авторы:
Масленников Никита Александрович, к.т.н., доцент.
tehmeh@spbgasu.ru
59