Похожие презентации:
Углы поворота. Градусная мера углов и дуг
1.
Углы поворота. Градусная мера углов и дуг.“+”
Алгебра , 9-10 класс
Воробьев Леонид Альбертович, г.Минск
2.
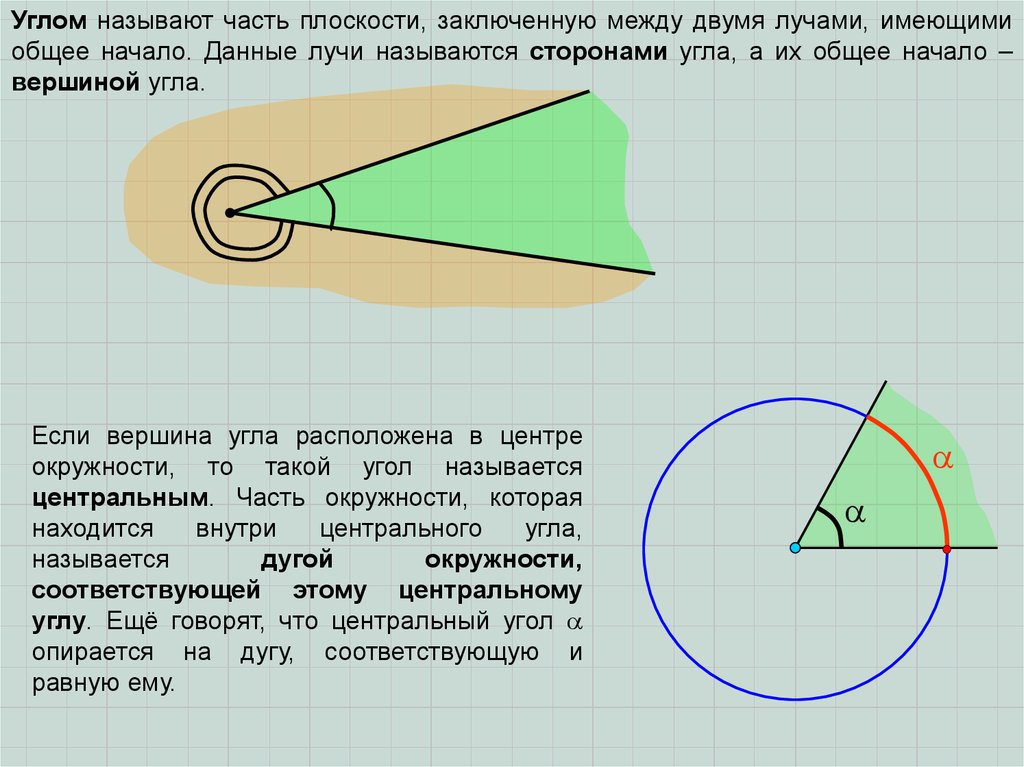
Углом называют часть плоскости, заключенную между двумя лучами, имеющимиобщее начало. Данные лучи называются сторонами угла, а их общее начало –
вершиной угла.
Если вершина угла расположена в центре
окружности, то такой угол называется
центральным. Часть окружности, которая
находится
внутри
центрального
угла,
называется
дугой
окружности,
соответствующей этому центральному
углу. Ещё говорят, что центральный угол
опирается на дугу, соответствующую и
равную ему.
3.
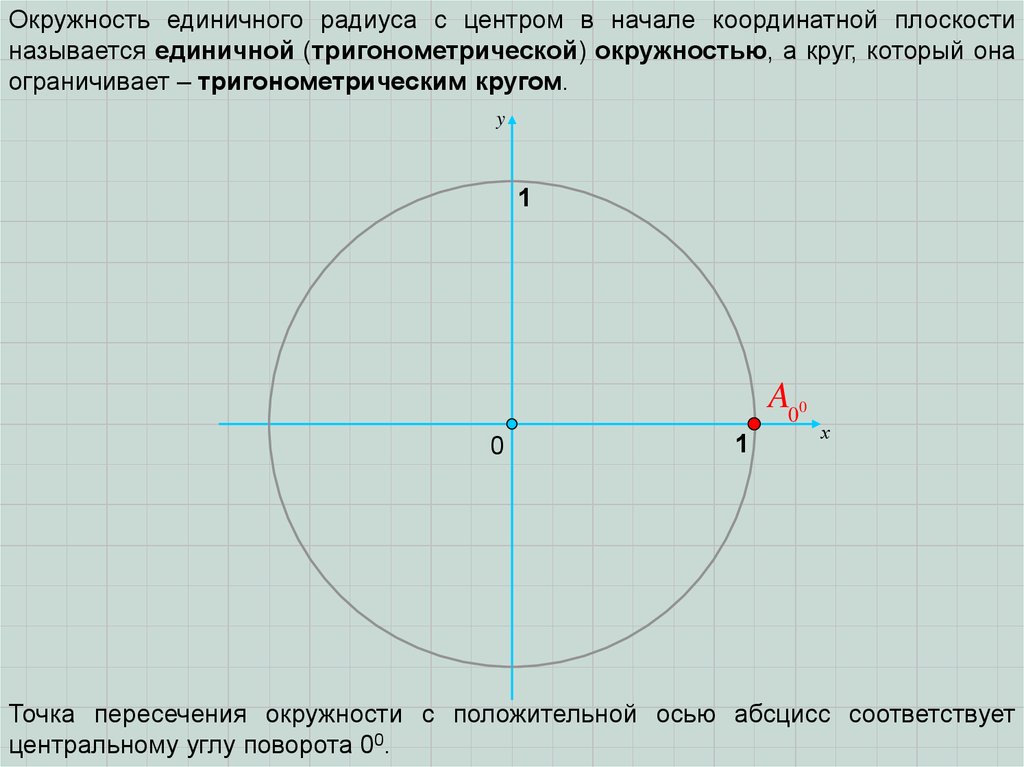
Окружность единичного радиуса с центром в начале координатной плоскостиназывается единичной (тригонометрической) окружностью, а круг, который она
ограничивает – тригонометрическим кругом.
y
1
A00
0
1
х
Точка пересечения окружности с положительной осью абсцисс соответствует
центральному углу поворота 00.
4.
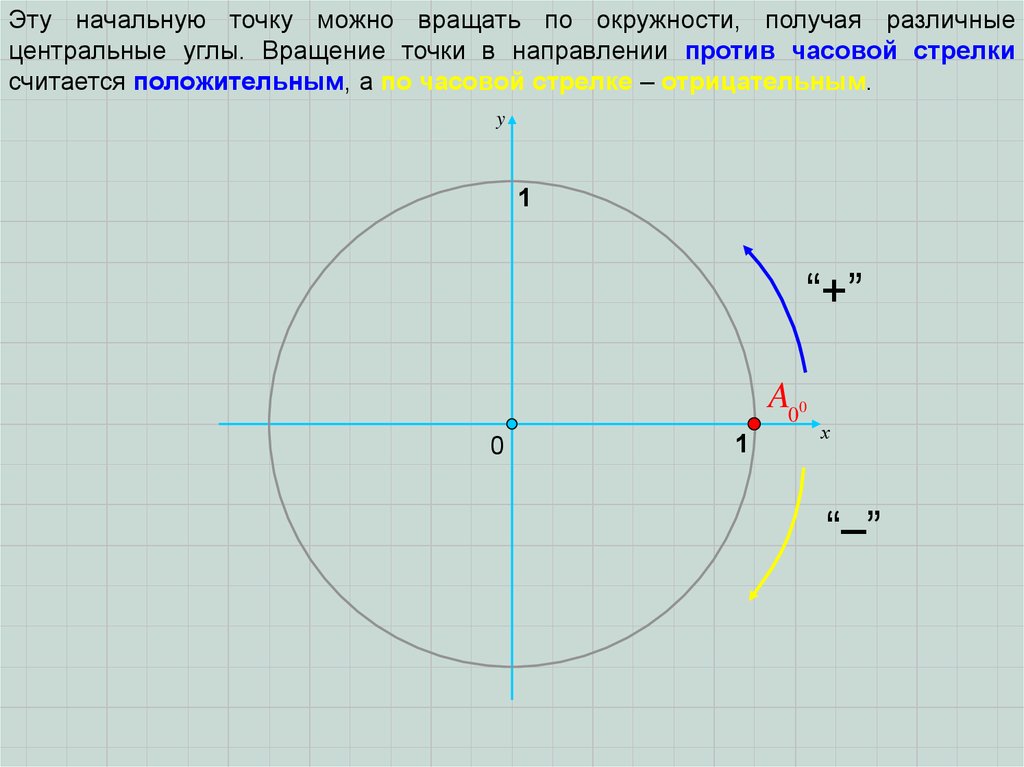
Эту начальную точку можно вращать по окружности, получая различныецентральные углы. Вращение точки в направлении против часовой стрелки
считается положительным, а по часовой стрелке – отрицательным.
y
1
“+”
A00
0
1
х
“–”
5.
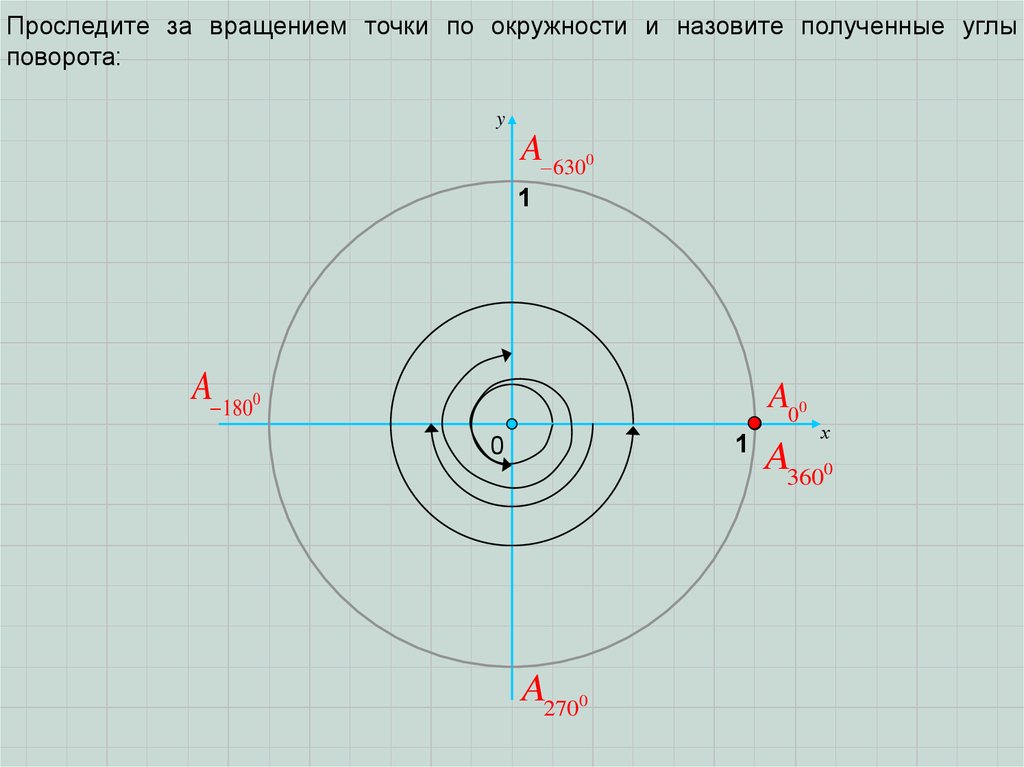
Проследите за вращением точки по окружности и назовите полученные углыповорота:
y
A 6300
1
A 1800
A00
1
0
A2700
х
A3600
6.
Если добавить полный поворот к острому углу α , то мы сноваокажемся в той же точке А. Но теперь она соответствует углу
поворота (подумайте)… 3600 .
Вообще, любую точку окружности можно получить поворотом на
вида α+3600·n, где n и α [0;3600).
угол,
y
ПРИМЕР.
1
Aα
Aα+3600
10200=3600·2+3000
1020 360
720 2
300
0
A0
1
x
7.
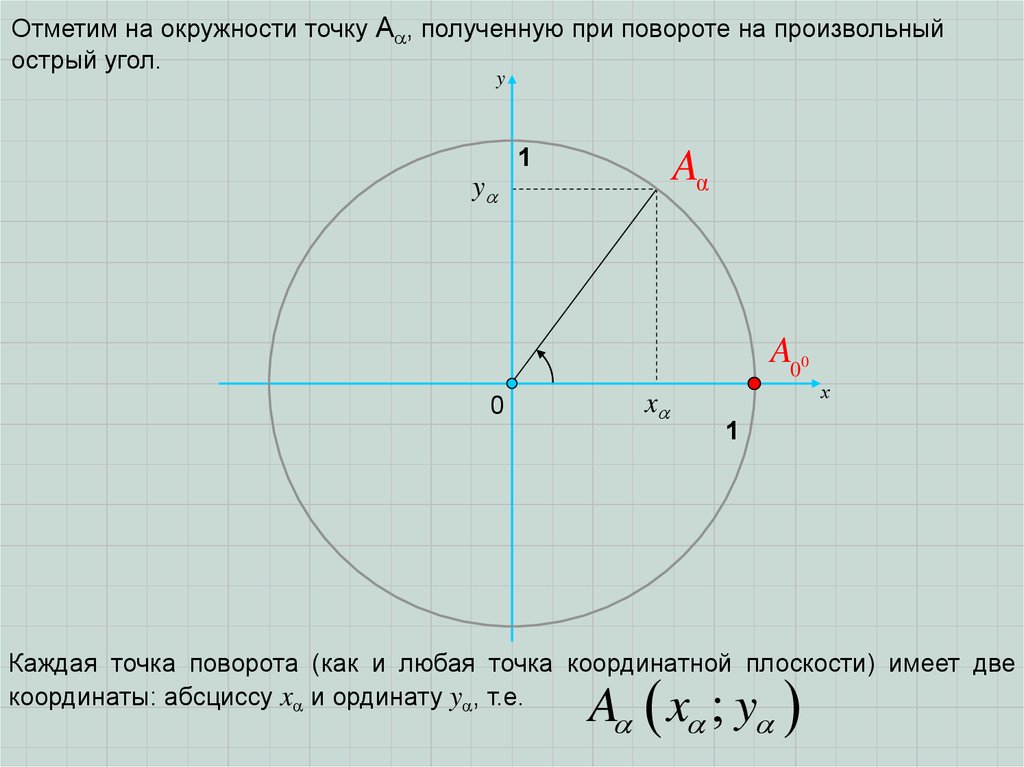
Отметим на окружности точку A , полученную при повороте на произвольныйострый угол.
y
1
Aα
y
A00
0
x
х
1
Каждая точка поворота (как и любая точка координатной плоскости) имеет две
координаты: абсциссу x и ординату y , т.е.
A x y
8.
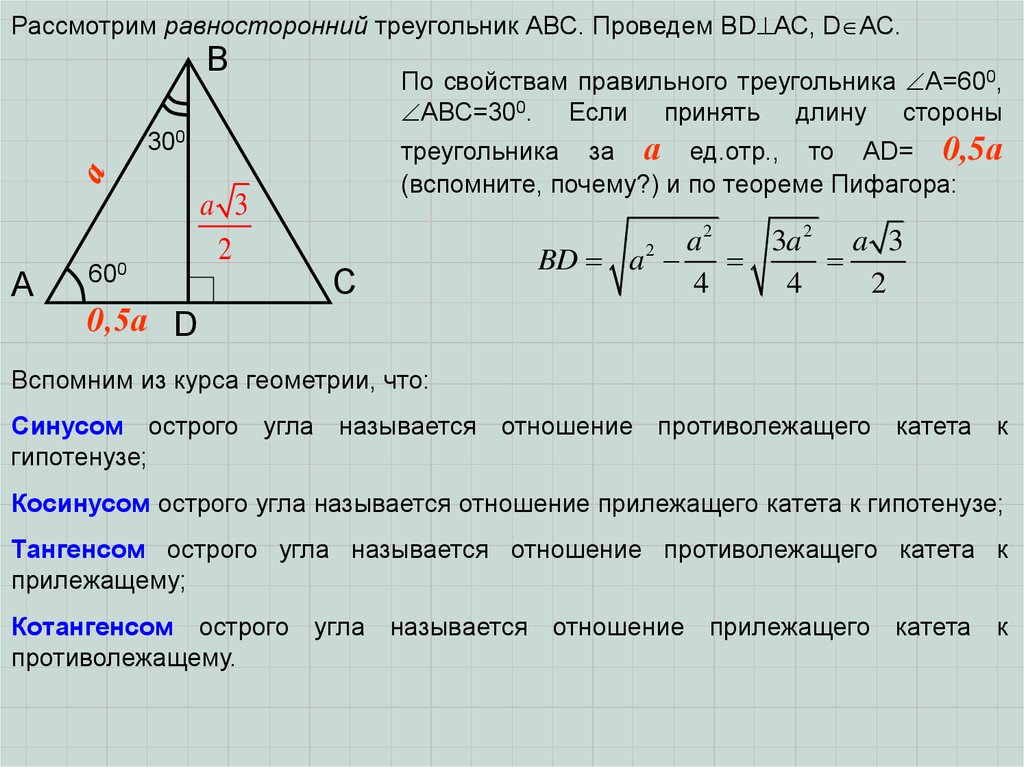
Рассмотрим равносторонний треугольник АВС. Проведем ВD АС, D АС.В
По свойствам правильного треугольника А=600,
АВС=300. Если принять длину стороны
треугольника за а ед.отр., то AD= 0,5а
(вспомните, почему?) и по теореме Пифагора:
300
А
600
a 3
2
С
2
2
a
3
a
a 3
BD a 2
4
4
2
0,5а D
Вспомним из курса геометрии, что:
Синусом острого угла называется отношение противолежащего катета к
гипотенузе;
Косинусом острого угла называется отношение прилежащего катета к гипотенузе;
Тангенсом острого угла называется отношение противолежащего катета к
прилежащему;
Котангенсом острого угла называется отношение прилежащего катета к
противолежащему.
9.
ВСинусом острого угла называется
противолежащего катета к гипотенузе;
Косинусом острого угла называется отношение
прилежащего катета к гипотенузе;
300
a 3
2
А
600
отношение
Тангенсом острого угла называется отношение
противолежащего катета к прилежащему;
С
0,5а D
Котангенсом острого угла называется отношение
прилежащего катета к противолежащему;
Из ΔABD, для углов 300 и 600, получим:
AD 0 ,5a 1
sin 30
AB
a
2
a 3
BD
3
co s 300
2
AB
a
2
0
tg 300
AD
a 3
1
3
0,5a :
BD
2
3
3
BD a 3
ctg 30
: 0,5a 3
AD
2
0
AD 0,5a 1
co s 60
AB
a
2
a 3
BD
3
sin 600
2
AB
a
2
0
ctg 600
AD
a 3
1
3
0,5a :
BD
2
3
3
BD a 3
tg 60
: 0 ,5a 3
AD
2
0
10.
Если рассматривать прямоугольный равнобедренный треугольник, то используяпредыдущие рассуждения, получим:
В
В= С=450. По теореме Пифагора:
BC a2 a2 2a2 a 2
450
а
a 2
И, тогда, по определению:
А
450
а
sin 450 a : a 2
С
1
2
2
2
1
2
co s 45 a : a 2
2 2
0
tg 450 a : a 1
ctg 450 a : a 1
11.
300sin
1
2
cos
3
2
3
3
tg
ctg
3
450
600
2
2
2
2
3
2
1
2
1
3
1
3
3
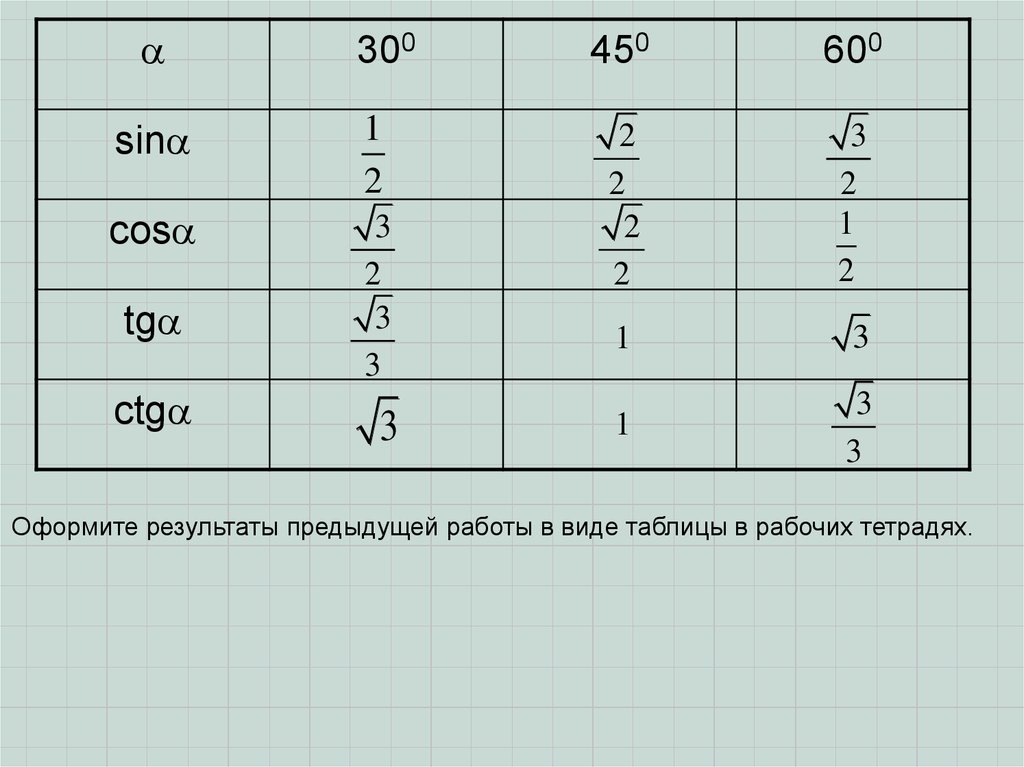
Оформите результаты предыдущей работы в виде таблицы в рабочих тетрадях.
12.
Координаты точек поворота II четверти:A1200
1
3
2
2
A1350
2
2
2
2
A1500
A1800
y
Координаты точек поворота I четверти:
A00 1
3 1
A300
2
2
900
1200
1350
3 1
1500
2 2
1 0
3
2
2
2
600
1
2
2
A450
2
2
450
300 A 1 3
60
1
2
0
A900
1800
–1
3
1
A2100
2
2
00
1
3
2
2
2
2
1
3
A2400
2
2
A2700 0 1
1
2
0
210
2
2
A2250
2
2
0
2250
2400
2
2
1
2
2
2
3
2
2700 –1
31
2
3150
3000
х
3600
3300
2 2
0 1
1
3
A3000
2
2
2
2
A3150
2
2
3
1
A3300
2
2
A3600 1 0
Самостоятельно определите точки поворота III и IV координатных четвертей и их
координаты…




 Математика
Математика








