Похожие презентации:
Методы интегрирования обыкновенных дифференциальных уравнений
1.
Чижова Ольга НиколаевнаК. 224 (кафедра теории управления)
chizhovolg@yandex.ru
o.chizhova@spbu.ru
2.
Литература:1. Н. М. Матвеев - Методы интегрирования
обыкновенных дифференциальных уравнений,
М., 1967.
2. А. П. Жабко, Е. Д. Котина, О. Н. Чижова –
Дифференциальные уравнения и устойчивость,
СПб, 2015.
3.
ВведениеДифференциальные уравнения – это математический аппарат, необходимый
для создания математических моделей изучаемых процессов и явлений,
которые непрерывно протекают во времени и параметры которых непрерывно
изменяются с течением времени.
1. Наблюдение за процессом или постановка эксперимента
2. Математическая форма записи процесса (создание математической модели)
3. Исследование математической модели
4. Физическая интерпретация выводов исследования
4.
Первая производная и первый дифференциалy f (x)
a
b
x
y f ( x0 x) f ( x0 )
y A x o( x)
A=A(x )
dy
A x
dx x
Функция, имеющая в некоторой точке первый дифференциал,
называется дифференцируемой в этой точке.
5.
f ( x0 x) f ( x0 )y ( x0 ) lim
x 0
x
Для того, чтобы функция одной переменной имела в некоторой точке
первый дифференциал, необходимо и достаточно, чтобы она
имела в этой точке конечную производную y ( x0 )
и было справедливо равенство
A( x0 ) y ( x0 )
dy y ( x0 )dx
dy
y
dx
6.
yz g ( x; y )
y
x
g
g ( x0 x; y0 ) g ( x0 ; y0 )
z x lim
x 0
x
x
g
g ( x0 ; y0 y ) g ( x0 ; y0 )
z y lim
y 0
y
y
x
7.
Z=h(x, y(x))dZ
dx






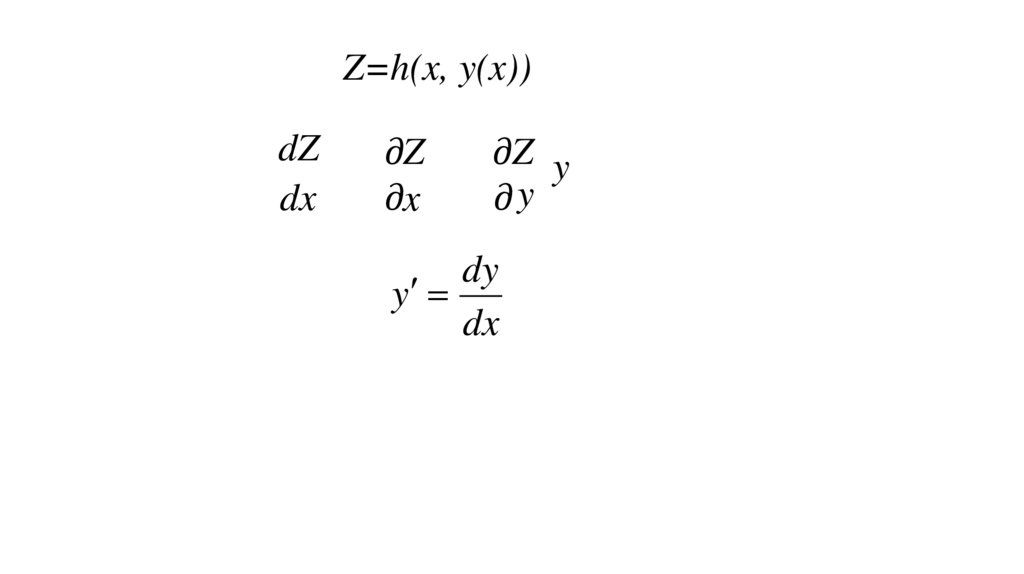
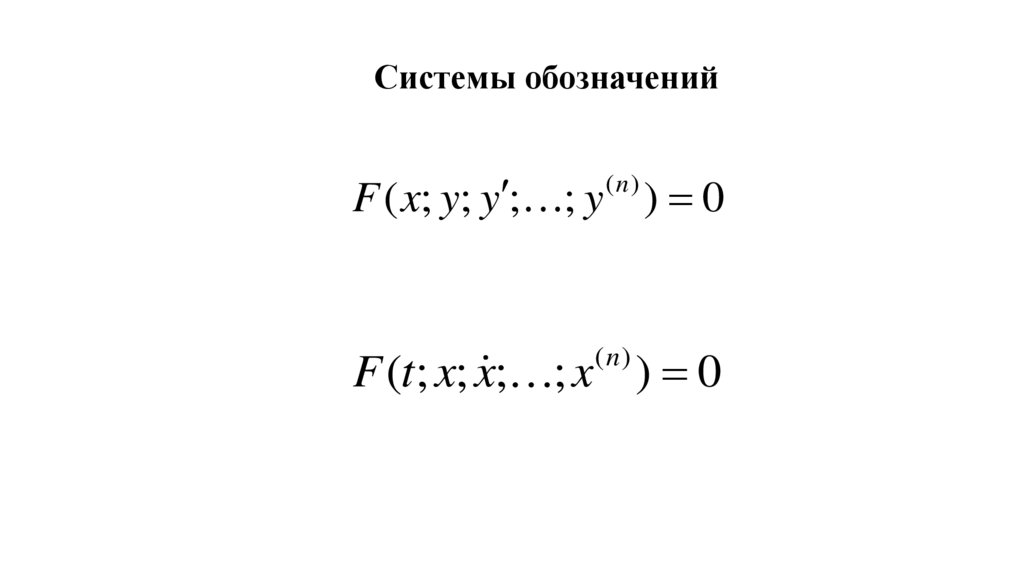







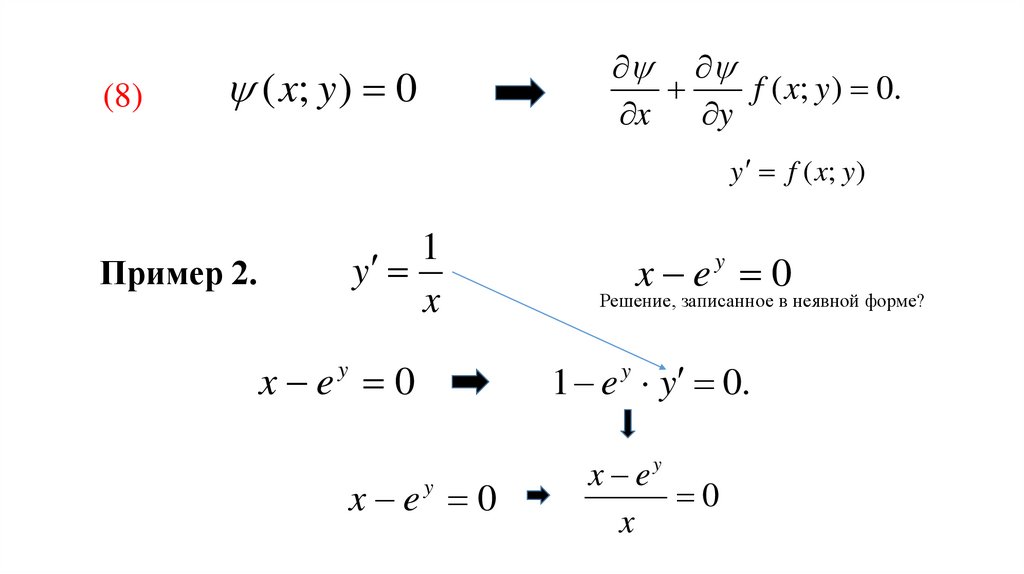

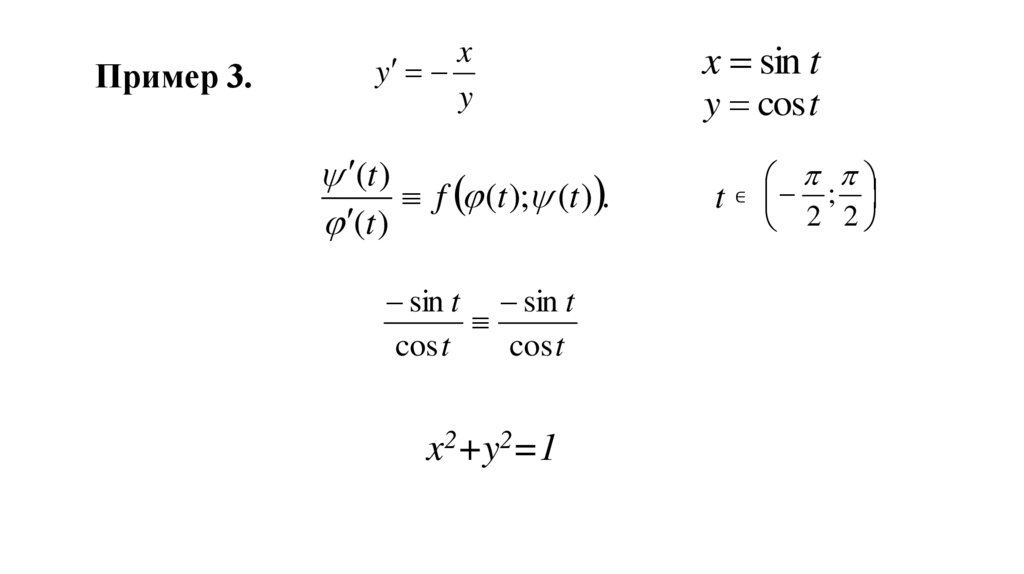

 Математика
Математика








