Геометрические задачи. Площадь треугольника

1.

Программирование – вторая грамотность.
А.П.Ершов
Математические основы
вычислительной геометрии

2.

Оглавление
Площадь треугольника
Площадь многоугольника
Задача о площади многоугольника
Ориентация треугольника
Задача о выпуклости многоугольника
Задача о штрафах за левый поворот
Задача о пересечении отрезков
Задача о расположении точки относительно
многоугольника
Расстояние от точки до прямой (плоскости)

3.

Вспомним!!!
a
h
b
Теорема. Площадь прямоугольной трапеции равна
половине
произведения
суммы
оснований на высоту.
S=1/2(a+b)h

4.

Площадь треугольника
Теорема.
Площадь треугольника, заданного на плоскости
координатами своих вершин (x1,y1), (x2,y2) и (x3,y3), равна
S=1/2|(x1-x2) (y1+y2)+ (x2-x3) (y2+y3)+ (x3-x1) (y3+y1)|

5.

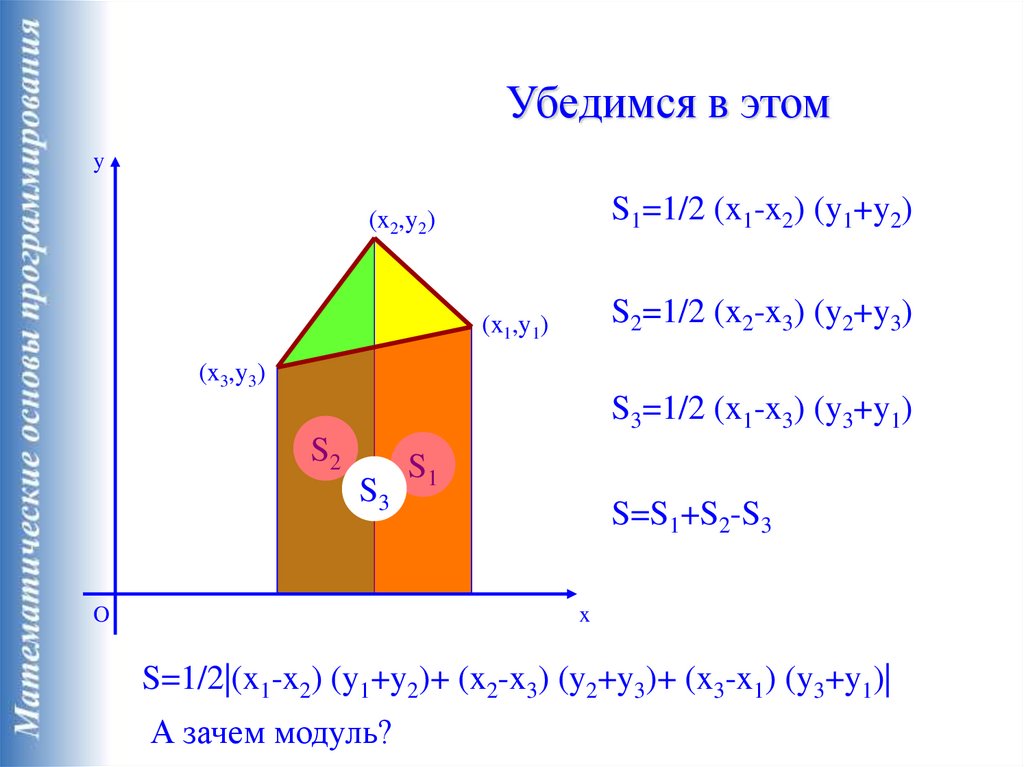
Убедимся в этом
y
S1=1/2 (x1-x2) (y1+y2)
(x2,y2)
S2=1/2 (x2-x3) (y2+y3)
(x1,y1)
(x3,y3)
S3=1/2 (x1-x3) (y3+y1)
S2
S3
O
S1
S=S1+S2-S3
x
S=1/2|(x1-x2) (y1+y2)+ (x2-x3) (y2+y3)+ (x3-x1) (y3+y1)|
А зачем модуль?

6.

Для другой ориентации треугольника
y
(x1,y1)
(x2,y2)
(x3,y3)
O
x
S=1/2|(x1-x2) (y1+y2)+ (x2-x3) (y2+y3)+ (x3-x1) (y3+y1)|
Какой вывод можно сделать, если S=0?

7.

Следствие
Три точки на плоскости с координатами (x1,y1), (x2,y2) и
(x3,y3) лежат на одной прямой тогда и только тогда, когда
(x1-x2) (y1+y2)+ (x2-x3) (y2+y3)+ (x3-x1) (y3+y1)=0

8.

Площадь многоугольника
Теорема.
Площадь
n-угольника,
заданного
на
плоскости
координатами своих вершин (x1,y1), (x2,y2), …, (xn,yn) в
порядке обхода, равна
S=1/2|(x1-x2) (y1+y2)+ (x2-x3) (y2+y3)+ … +(xn-1-xn) (yn-1+yn)+
+(xn-x1) (yn+y1)|

9.

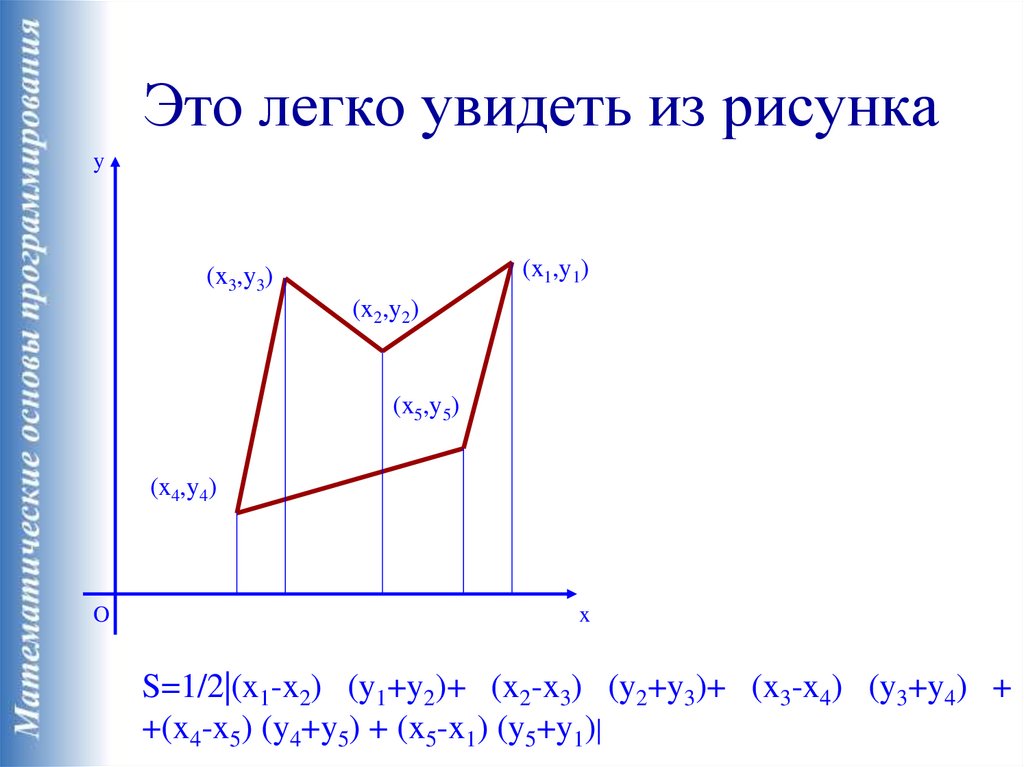
Это легко увидеть из рисунка
y
(x1,y1)
(x3,y3)
(x2,y2)
(x5,y5)
(x4,y4)
O
x
S=1/2|(x1-x2) (y1+y2)+ (x2-x3) (y2+y3)+ (x3-x4) (y3+y4) +
+(x4-x5) (y4+y5) + (x5-x1) (y5+y1)|

10.

Задача о площади многоугольника
Найти площадь многоугольника,
заданного на плоскости координатами
своих вершин в порядке обхода.
Ваша программа должна запросить
число вершин, координаты каждой
вершины, затем вычислить и
сообщить площадь многоугольника.

11.

Математическая модель
Аргументы
n – число сторон (вершин) многоугольника, целое,
большее 2
x[1..n+1] – абсциссы вершин, вещественные
y[1..n+1] – ординаты вершин, вещественные
x[n+1]:=x[1], y[n+1]=y[1]
Результаты
S – площадь многоугольника, вещественное
Промежуточные величины
i – счетчик цикла, целое

12.

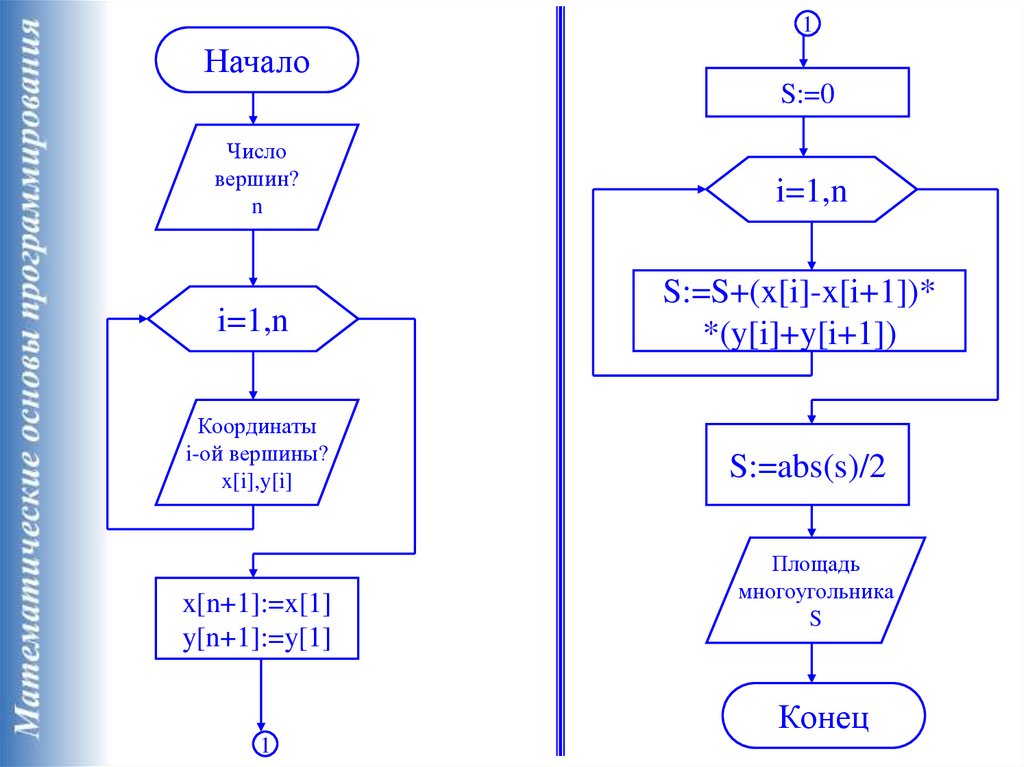
1
Начало
S:=0
Число
вершин?
n
i=1,n
Координаты
i-ой вершины?
x[i],y[i]
x[n+1]:=x[1]
y[n+1]:=y[1]
i=1,n
S:=S+(x[i]-x[i+1])*
*(y[i]+y[i+1])
S:=abs(s)/2
Площадь
многоугольника
S
Конец
1

13.

Рассмотрим выражение
F=(x1-x2) (y1+y2)+ (x2-x3) (y2+y3)+ (x3-x1) (y3+y1)
Оно представляет собой удвоенную
площадь треугольника со знаком.
Оказывается знак этого выражения несет
очень важную информацию о
треугольнике.
Сформулируем новую теорему.

14.

Ориентация треугольника
Теорема.
Треугольник,
заданный
на
плоскости
координатами своих вершин (x1,y1), (x2,y2) и
(x3,y3) ориентирован
против часовой стрелки, если
(x1-x2) (y1+y2)+ (x2-x3) (y2+y3)+ (x3-x1) (y3+y1)>0
по часовой стрелке, если
(x1-x2) (y1+y2)+ (x2-x3) (y2+y3)+ (x3-x1) (y3+y1)<0

15.

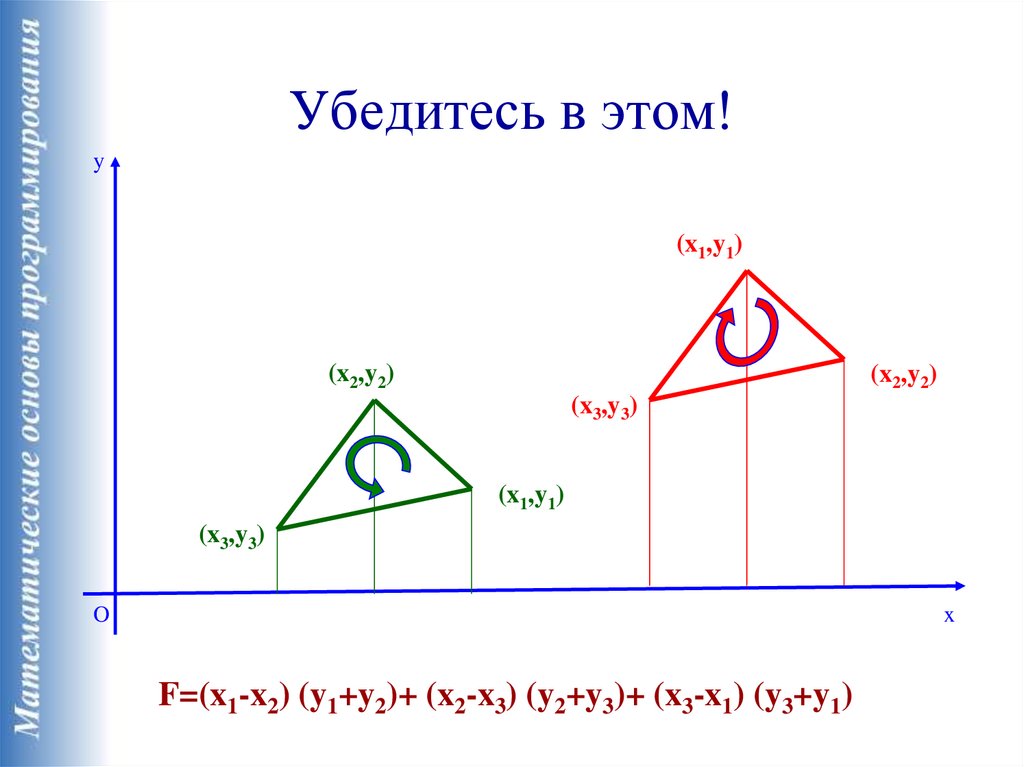
Убедитесь в этом!
y
(x1,y1)
(x2,y2)
(x2,y2)
(x3,y3)
(x1,y1)
(x3,y3)
O
x
F=(x1-x2) (y1+y2)+ (x2-x3) (y2+y3)+ (x3-x1) (y3+y1)

16.

Задача о выпуклости многоугольника
На плоскости заданы n точек своими координатами,
являющиеся вершинами замкнутого многоугольника.
Координаты точек заданы в порядке обхода вершин по
границе многоугольника. Определить является ли
многоугольник выпуклым.
На входе программы задается число n (n<10) и массивы
координат. На выходе ответ – да или нет. Данные вводятся с
клавиатуры.
Примеры
Вход
n=7
{(0,0); (–2,3); (0,5); (4,5); (5,4); (5,2); (3,0)}
n=6
{(–3,1); (–1,2); (–2,3); (2,2); (3,0); (0,–1)}
Выход
да
нет

17.

Математическая модель
Аргументы
n – число сторон (вершин) многоугольника, целое, большее 2
x[1..n+2] – абсциссы вершин, вещественные
y[1..n+2] – ординаты вершин, вещественные
x[n+1]:=x[1], y[n+1]=y[1]
x[n+2]:=x[2], y[n+2]=y[2]
Результаты
t - строковая константа для ответа, принимающая значения «да» или
«нет» (или логическая переменная – true или false)
Промежуточные величины
i – счетчик цикла, целое
z, z1 – значения функции F для трех подряд вершин многоугольника,
вещественное

18.

2
2
3
3
1
1
4
6
5
5
4
6
У выпуклого многоугольника
У невыпуклого многоугольника
все треугольники из соседних
вершин 123, 234, 345, 456, 561,
612
среди треугольников из соседних
вершин 123, 234, 345, 456, 561,
612
одинаковой ориентации
есть
треугольники
ориентации
разной

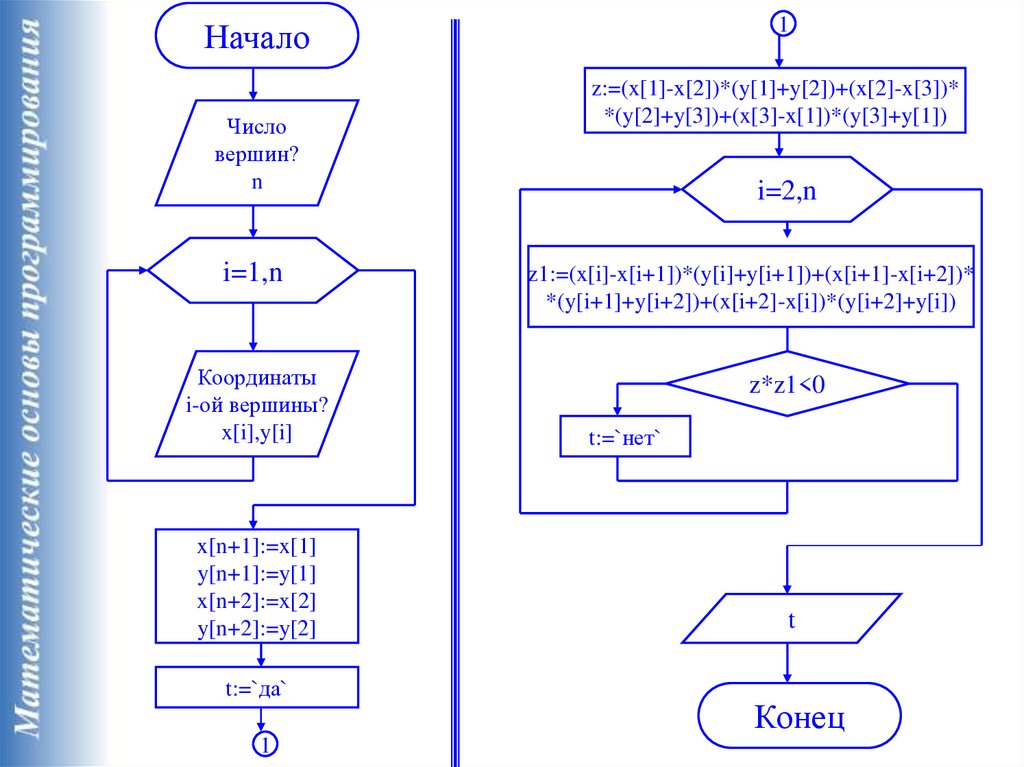
19.

1
Начало
Число
вершин?
n
i=1,n
Координаты
i-ой вершины?
x[i],y[i]
x[n+1]:=x[1]
y[n+1]:=y[1]
x[n+2]:=x[2]
y[n+2]:=y[2]
t:=`да`
1
z:=(x[1]-x[2])*(y[1]+y[2])+(x[2]-x[3])*
*(y[2]+y[3])+(x[3]-x[1])*(y[3]+y[1])
i=2,n
z1:=(x[i]-x[i+1])*(y[i]+y[i+1])+(x[i+1]-x[i+2])*
*(y[i+1]+y[i+2])+(x[i+2]-x[i])*(y[i+2]+y[i])
z*z1<0
t:=`нет`
t
Конец

20.

Задача о левых поворотах
Новый градоначальник города Н.Глупова решил с целью пополнения
бюджета и экономии горючего провести компанию борьбы с "левым
уклоном". Для этого он запретил водителям выполнять левые повороты,
установив за каждый такой поворот штраф в размере одного МРОТ.
Кроме этого, он приказал установить компьютерную систему тотальной
слежки за автомобилями, которая фиксирует координаты каждого
автомобиля в начале и в конце его движения, а также в те моменты,
когда автомобиль выполняет какой–либо поворот.
От тяжелого прошлого городу Н.Глупову достались улицы в
плохом состоянии, которые, кроме того, могут пересекаться под любыми
углами. Развороты новый градоначальник не запретил.
Задание:
Написать программу, которая по заданной последовательности
координат движения автомобиля вычисляет штраф .

21.

Для создания математической модели учтите, что
левый поворот порождает треугольник,
ориентированный против часовой стрелки.

22.

Задача о пересечении отрезков
Два отрезка заданы координатами своих
концов. Определить, пересекаются ли
они во внутренней точке.

23.

C
B
C
B
D
A
A
D
2
1
C
D
C
B
B
A
4
Сравните ориентацию пар треугольников
CAB и DAB
и
BCD и ACD
в приведенных примерах. Сделайте вывод.
D
A
3

24.

Задача о расположении точки
относительно выпуклого
многоугольника
Выпуклый многоугольник задан
координатами своих вершин.
Определить, является ли точка M с
координатами (a,b) внутренней точкой
многоугольника.

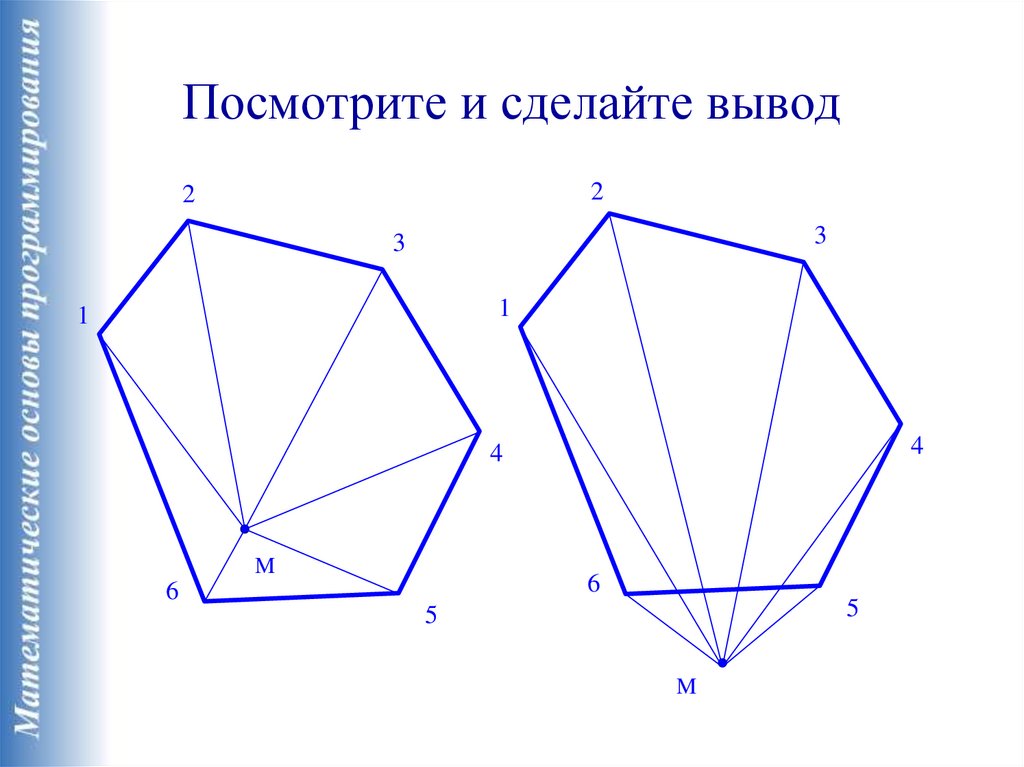
25.

Посмотрите и сделайте вывод
2
2
3
3
1
1
4
4
M
6
6
5
5
M

26.

Расстояние от точки до прямой.
Теорема.
Расстояние от точки
ax+by+c=0 равно
M(x1,y1)
до
прямой

27.

Расстояние от точки до плоскости.
Теорема.
Расстояние от точки M(x1,y1,z1) до плоскости
ax+by+cz+d=0 равно

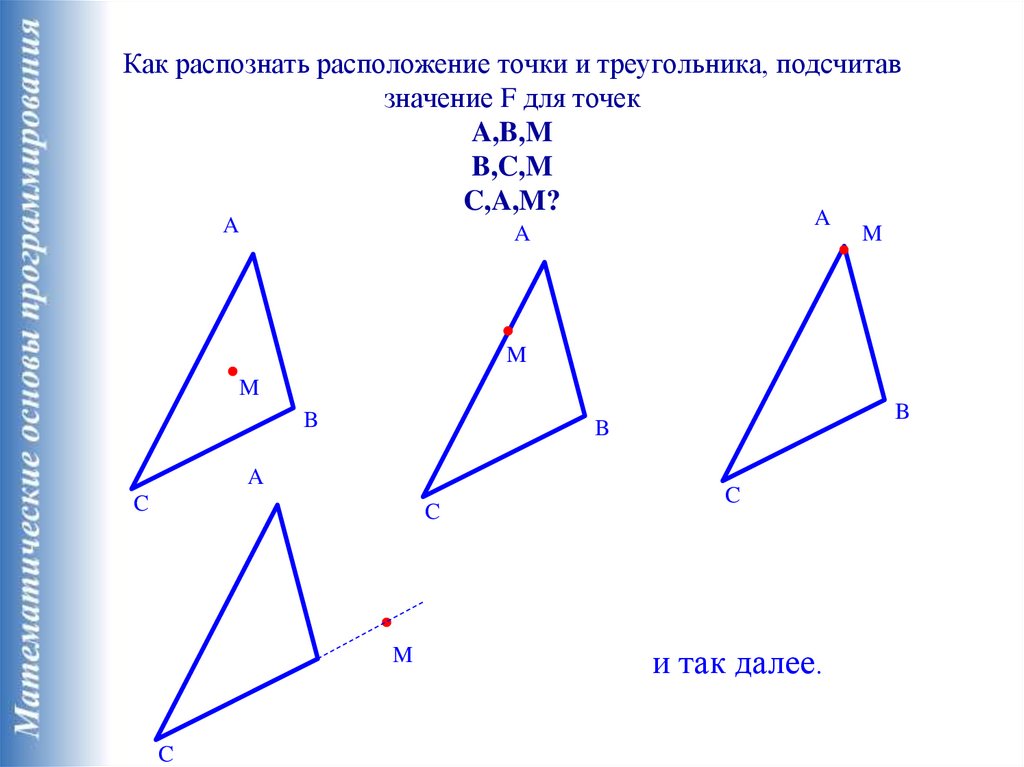
28.

Как распознать расположение точки и треугольника, подсчитав
значение F для точек
A,B,M
B,C,M
C,A,M?
A
A
A
M
M
M
B
A
C
C
M
C
B
B
C
и так далее.