Расстояния в пространстве (расстояние от точки до прямой, расстояние от точки до плоскости, расстояние между прямыми)

1. Расстояния в пространстве ( расстояние от точки до прямой, расстояние от точки до плоскости, расстояние между скрещивающимися

прямыми).
Подготовила учитель математики МБОУ
«СОШ №18» г. Энгельса
Пастухова Наталья Алексеевна

2. Цели и задачи:

Цель :
систематизировать знания по решению задач на
нахождение расстояний в пространстве методами,
изучаемыми в средней школе, а также методами,
которым в школе по тем или иным причинам не
уделяется должное внимание.
Задачи:
рассмотреть теоретический материал, различные
методы и приемы, применяемые при решении задач
на нахождение расстояний в пространстве;
привести примеры решения задач, взятых из
различных источников, и задач из вариантов ЕГЭ.

3. Расстояние от точки до прямой.

Определения:
Расстояние от точки до прямой, не содержащей
эту точку, есть длина отрезка перпендикуляра,
проведенного из этой точки на прямую.
Расстояние между двумя параллельными
прямыми равно длине отрезка их общего
перпендикуляра.
Расстояние между двумя параллельными
прямыми равно расстоянию от любой точки одной
из этих прямых до другой прямой.

4. Поэтапно-вычислительный метод.

Расстояние от точки до прямой можно
вычислить, как длину отрезка
перпендикуляра, если удается включить
этот отрезок в некоторый треугольник в
качестве одной из высот.

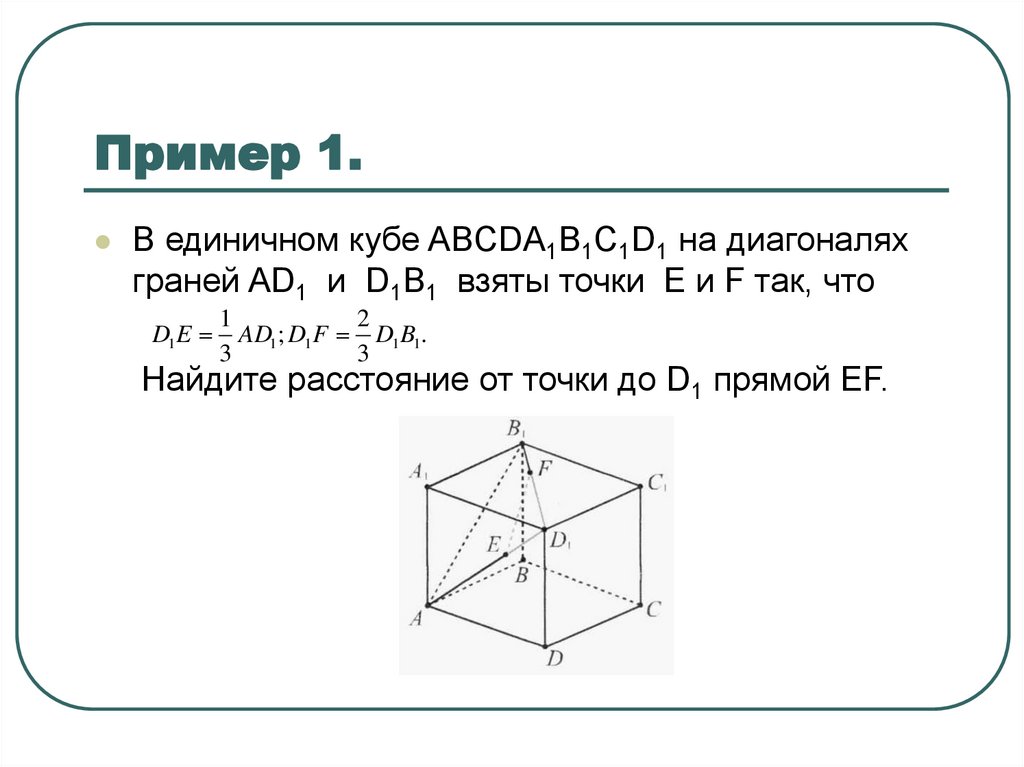
5. Пример 1.

В единичном кубе ABCDA1B1C1D1 на диагоналях
граней AD1 и D1B1 взяты точки E и F так, что
D1 E
1
2
AD1 ; D1 F D1 B1.
3
3
Найдите расстояние от точки до D1 прямой EF.

6. Координатный метод.

Вводят декартову систему координат, начало
координат совмещают с одной из вершин, оси,
выходящие из этой вершины, направлены вдоль
ребер многогранника, и проводят все вычисления
в координатной форме.
Пример 2. В единичном кубе ABCDA1B1C1D1
найти расстояние от точки D1 до прямой PQ, где
P и Q – середины соответственно ребер A1B1 и
BC.

7. Векторный метод.

Обычно при решении задач, в которых рассматривается
призма или пирамида, в качестве базисных векторов
выбирают какую либо тройку векторов, выходящих из одной
вершины и направленных вдоль ребер многогранника.
Пример 3. В единичном кубе ABCDA1B1C1D1 найти
расстояние от точки D1 до прямой PQ, где P и Q –
середины соответственно ребер A1B1 и BC.
Решение.
Пусть
тогда
AD a , AB b , AA1 c ,
a b c 1, a b a c b c 0

8. Расстояние от точки до плоскости.

Определения:
Расстояние от точки до плоскости, не содержащей
эту точку, есть длина отрезка перпендикуляра,
опущенного из этой точки на плоскость.
Расстояние между прямой и параллельной ей
плоскостью равно длине их общего перпендикуляра.
Расстояние между прямой и параллельной ей
плоскостью равно расстоянию от любой точки этой
прямой до плоскости.
Расстояние между двумя параллельными
плоскостями равно длине их общего перпендикуляра.
Расстояние между двумя параллельными
плоскостями равно расстоянию между точкой одной
из этих плоскостей и другой плоскостью.

9. Поэтапно- вычислительный метод.

Расстояние от точки Т до плоскости α можно найти
руководствуясь следующим планом: (см. рис. 208)
Выберем в плоскости α какую-нибудь прямую р и из
точки Т опустим перпендикуляр TR на эту прямую;
В плоскости α через точку R проведем прямую q p;
Найдем расстояние от точки Т до прямой q. Это TH расстояние от точки Т до плоскости α.

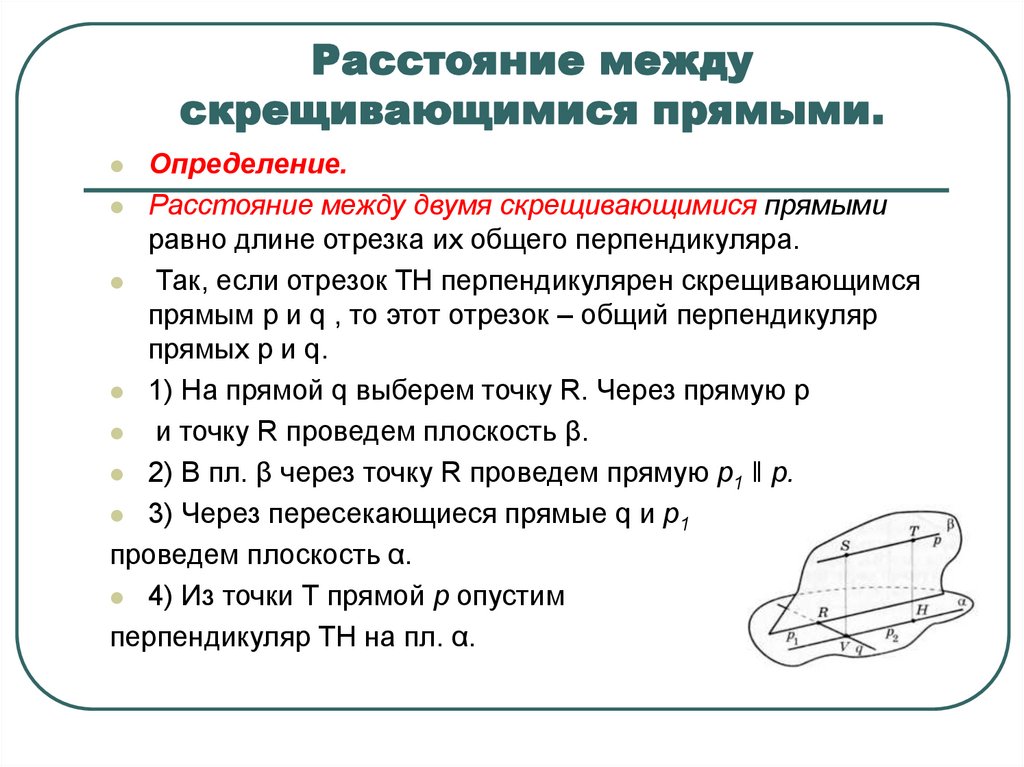
10. Расстояние между скрещивающимися прямыми.

Определение.
Расстояние между двумя скрещивающимися прямыми
равно длине отрезка их общего перпендикуляра.
Так, если отрезок TH перпендикулярен скрещивающимся
прямым p и q , то этот отрезок – общий перпендикуляр
прямых p и q.
1) На прямой q выберем точку R. Через прямую p
и точку R проведем плоскость β.
2) В пл. β через точку R проведем прямую р1 ǁ р.
3) Через пересекающиеся прямые q и р1
проведем плоскость α.
4) Из точки Т прямой р опустим
перпендикуляр TH на пл. α.

11. Расстояние между скрещивающимися прямыми (четыре способа) .

Построить общий перпендикуляр двух скрещивающихся прямых
(отрезок с концами на этих прямых и перпендикулярный обеим)
и найти его длину.
Построить плоскость, содержащую одну из прямых и
параллельную второй. Тогда искомое расстояние будет равно
расстоянию от какой-нибудь точки второй прямой до
построенной плоскости.
Заключить данные скрещивающиеся прямые в параллельные
плоскости и найти расстояние между этими плоскостями.
Построить плоскость, перпендикулярную одной из данных
прямых, и построить на этой плоскости ортогональную проекцию
второй прямой. Расстояние между проекциями прямых на эту
плоскость равно расстоянию между скрещивающимися
прямыми.

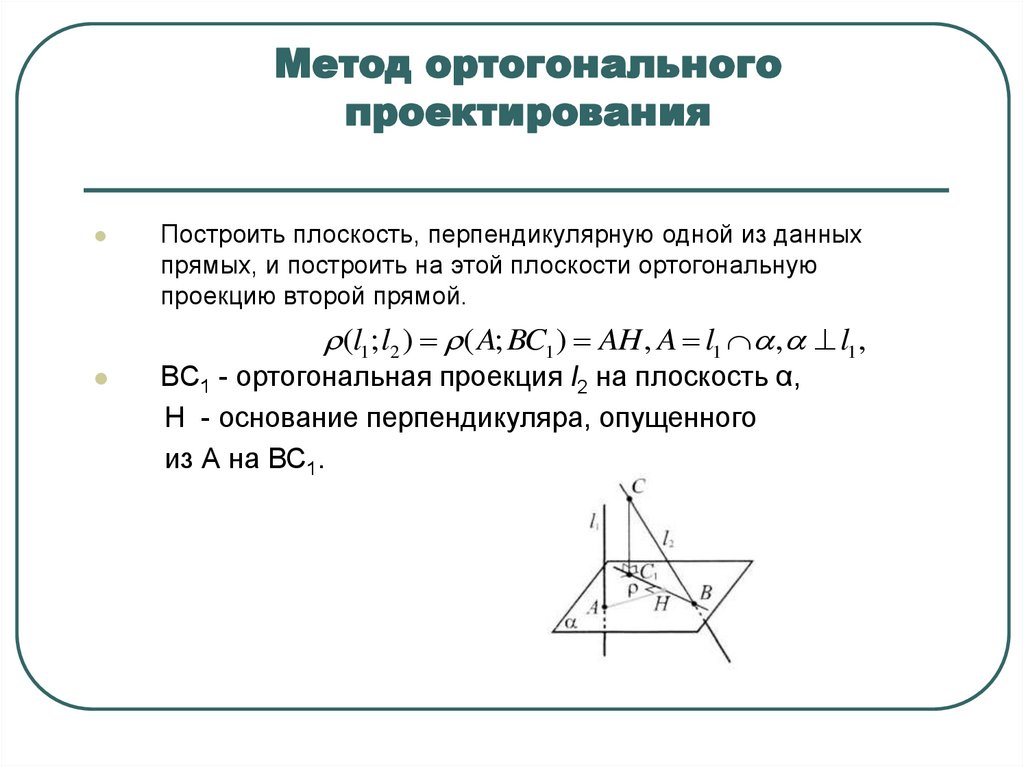
12. Метод ортогонального проектирования

Построить плоскость, перпендикулярную одной из данных
прямых, и построить на этой плоскости ортогональную
проекцию второй прямой.
(l1; l2 ) ( A; BC1 ) AH , A l1 , l1,
BC1 - ортогональная проекция l2 на плоскость α,
H - основание перпендикуляра, опущенного
из А на ВС1.

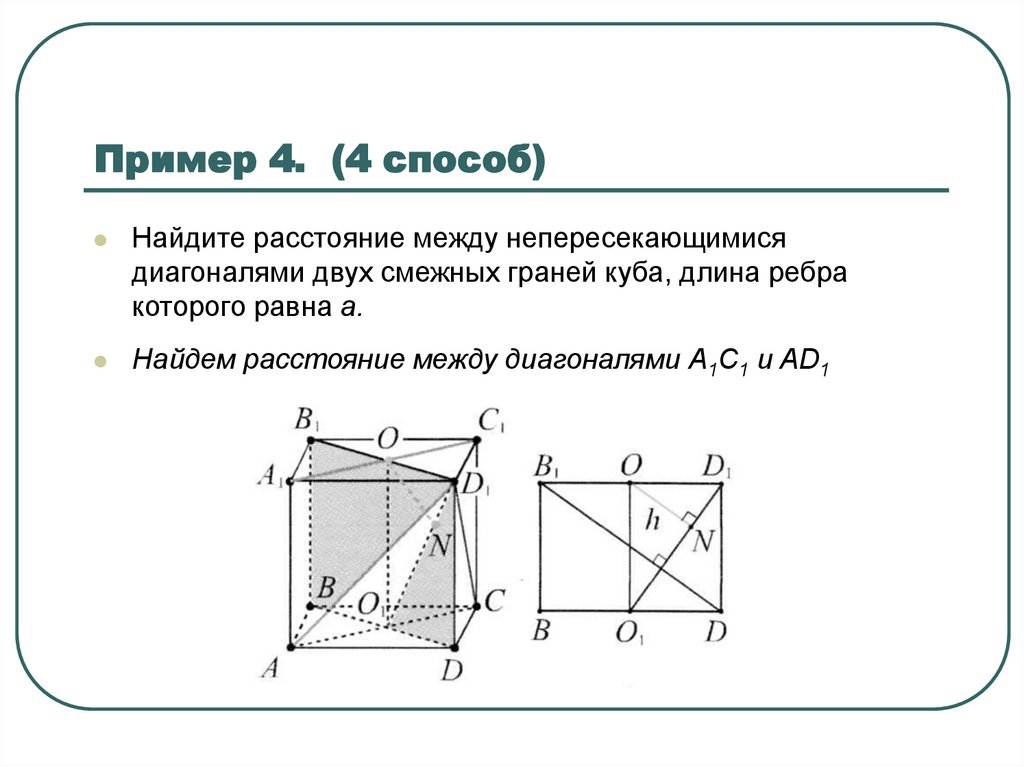
13. Пример 4. (4 способ)

Найдите расстояние между непересекающимися
диагоналями двух смежных граней куба, длина ребра
которого равна а.
Найдем расстояние между диагоналями А1С1 и AD1

14. 1 способ

Найдите расстояние между непересекающимися
диагоналями двух смежных граней куба, длина ребра
которого равна а.
Найдем расстояние между диагоналями А1С1 и AD1

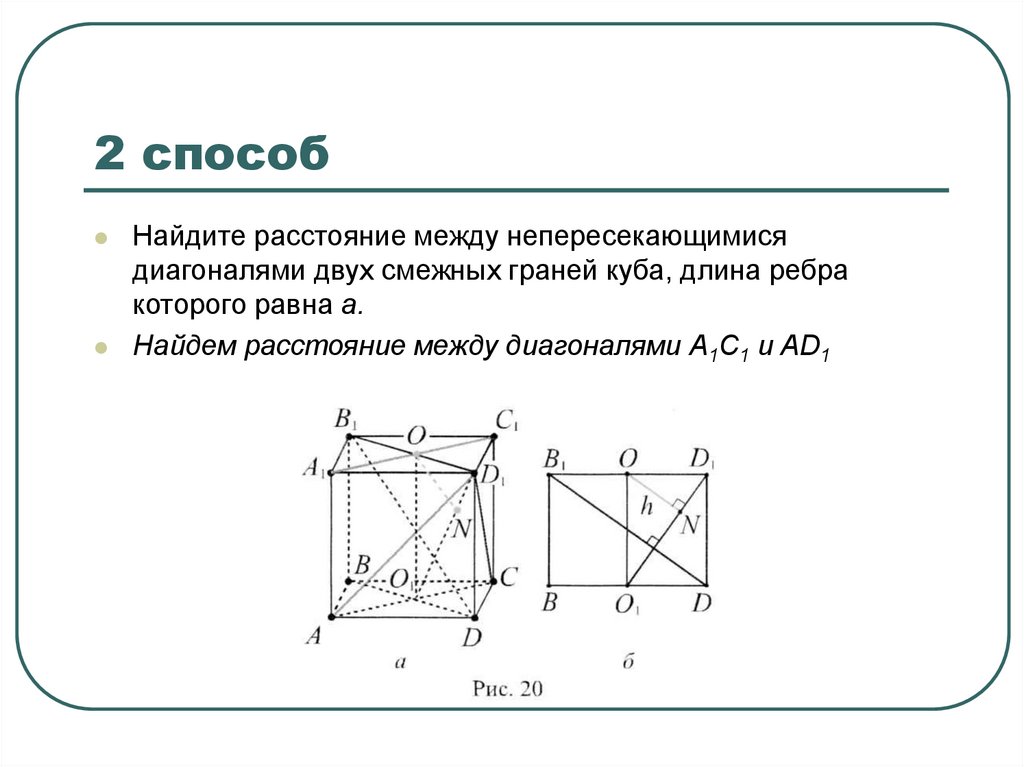
15. 2 способ

Найдите расстояние между непересекающимися
диагоналями двух смежных граней куба, длина ребра
которого равна а.
Найдем расстояние между диагоналями А1С1 и AD1

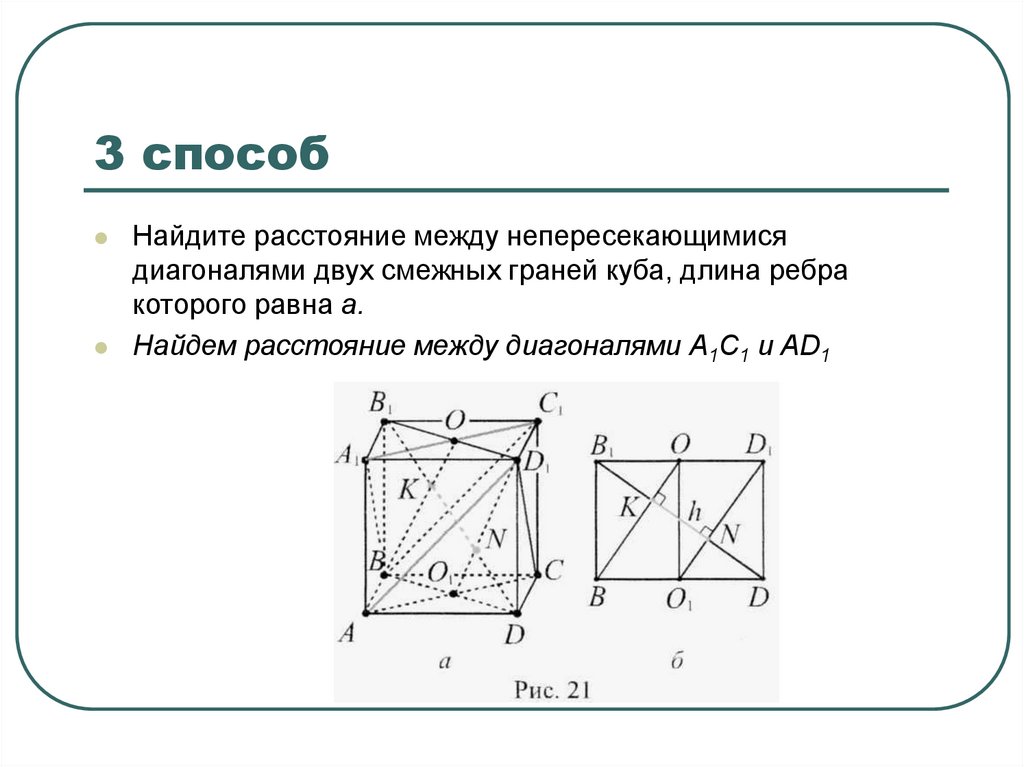
16. 3 способ

Найдите расстояние между непересекающимися
диагоналями двух смежных граней куба, длина ребра
которого равна а.
Найдем расстояние между диагоналями А1С1 и AD1

17. Список используемой литературы

Книги
1.1 Литвиненко В.Н., Батугина О.А. Геометрия. Готовимся к ЕГЭ.
Пособие для учащихся общеобразовательных учреждений. –М.:
Просвещение, 2011. – 158 с.
1.2 Сагателова Л.С., В.Н. Студенецкая В.Н. Практическая
геометрия. Комбинации геометрических тел, 10 - 11классы.
Методическое пособие. – М.: Планета, 2011. -334 с.
1.3 Орехова А.И. Задачи на готовых чертежах. Стереометрия.
Практикум для учащихся общеобразовательных учреждений. –
Мозырь: Белый ветер, 2010. – 50 с.
Статьи
2.1 Корянов А.Г., Прокофьев А.А. Многогранники: виды
задач и методы их решения. МИЭТ «Абитуриенту 2011». – 89 с.