Расстояния в пространстве. Расстояние между двумя точками

1. Расстояния в пространстве

2. Расстояние между двумя точками

3.

Найдите расстояние между точками Р и Н –
серединами скрещивающихся рёбер:
а) куба с ребром, равным а;
Задача 1.
Решение.
а) (рис. 1)
РК АD, АK =
KD
∆РКН
K = 90 , РK = а
KH
1
a 2
DB
2
2
2
2
a
a 6
2
a PH
2
P
,
H
a
B
4
2
2
2a 2 a 6
H a
Ответ:4
2
2

4. Задача 2. Найдите расстояние между точками Р и Н – серединами скрещивающихся рёбер: б) тетраэдра, все рёбра которого равны а.

Найдите расстояние между точками Р и Н –
серединами скрещивающихся рёбер:
б) тетраэдра, все рёбра которого равны а.
Задача 2.
AOS , O 90
AOS ,AS Oa , 90AO
o
AS a,
a
AO
2
2 3 a
o
a
3
AOS , O 90 o
AS a,
AO
a
3
2
a 2 SO a 2 a a 2
SO 2 a
3
3
a
a 23
3
2
SO a
o
o
3
PKH
,
K
90
3
PKH , K 90
PKH , K1 90 o
1
a
a
PK
SO
1PK aSO
2
6
PK SO 2
6
2
6
a
a
KH AO
aAO
KH
KH AO
3
3
3
2
2
2
a
a
a
2
2a 2
a PH
a
a
aa
PH
PH Ответ:
6
3
2
6
3 6 23
2

5. Расстояние между фигурами

Если среди всех расстояний между точками, одна из
которых принадлежит фигуре F1, а другая - фигуре F2,
существует наименьшее, то его называют расстоянием
между фигурами F1 и F2.

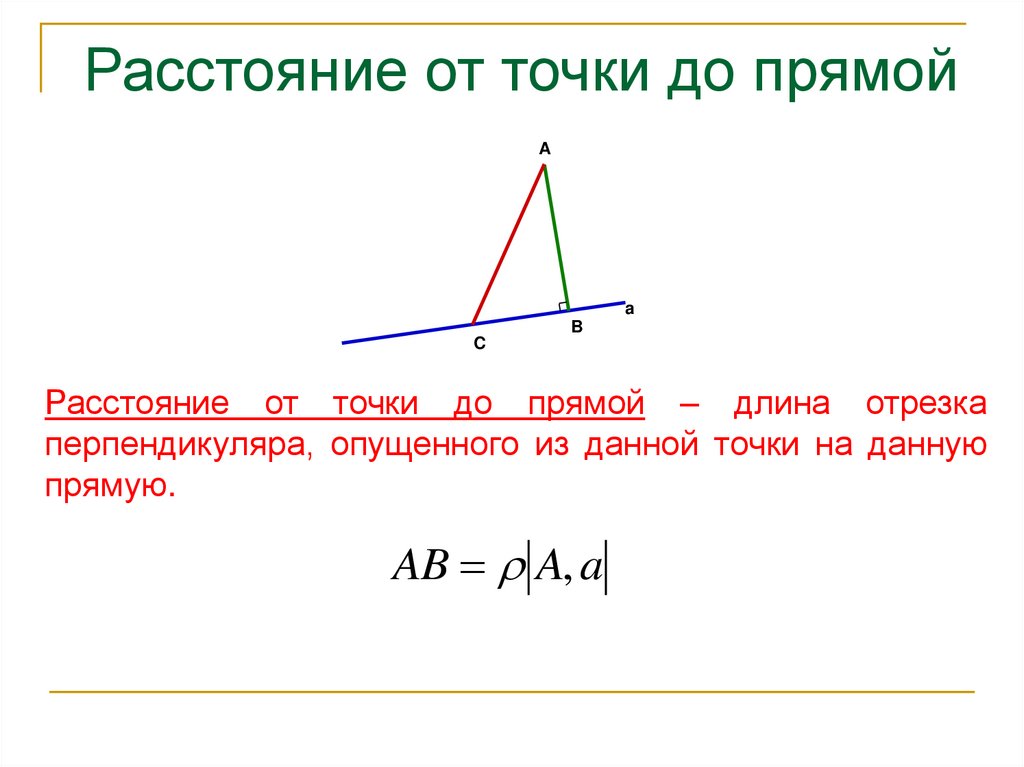
6. Расстояние от точки до прямой

A
a
B
C
Расстояние от точки до прямой – длина отрезка
перпендикуляра, опущенного из данной точки на данную
прямую.
AB A, a

7. Расстояние от точки до плоскости

A
B
C
.
pис.12
Расстояние от точки до плоскости – длина отрезка
перпендикуляра, опущенного из данной точки на данную
плоскость.
A, AB

8.

Пусть надо найти расстояние от точки А до плоскости β и
пусть точка А лежит в плоскости α, α∩β= с.
Проведём АВ с, ВP c, (α,β) = PBC, AN PB.
c AB
c PB
c ( PBA),
AB PB B
AN c
AN ( PBA), , c AN
AN PB AN , , A, AN
c PB B

9. Расстояние между двумя прямыми

a, b 0
a, b MN

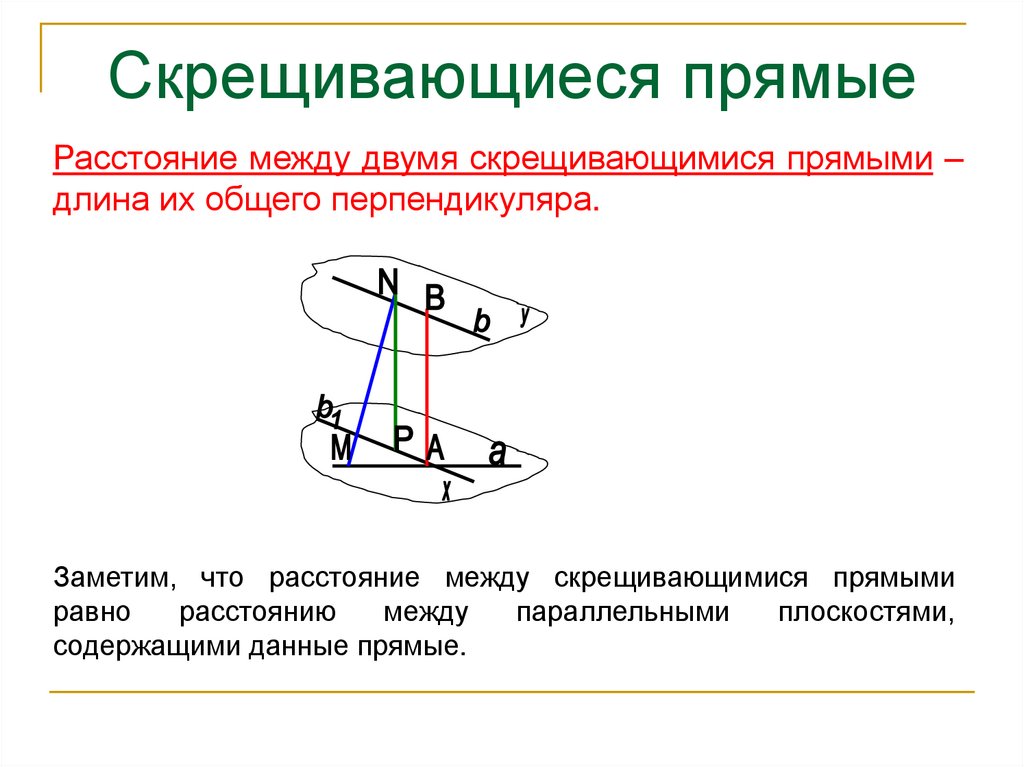
10. Скрещивающиеся прямые

Расстояние между двумя скрещивающимися прямыми –
длина их общего перпендикуляра.
Заметим, что расстояние между скрещивающимися прямыми
равно
расстоянию
между
параллельными
плоскостями,
содержащими данные прямые.

11.

Задача № 7. (рис.19) Дан куб ABCDA1B1C1D1. Постройте общий
перпендикуляр прямых A1D и ВС1.
Найдите расстояние между прямыми, если ребро куба равно а.
D1
C1
B1
A1
MN AD1, MN B C1,
N
M
D
A
AD1 ∩ DA1 = M, BC1 ∩ CB1 = N,
C
B
MN = |A1D,BC1|, MN = a.

12. Решение задач