Похожие презентации:
Числа, вычисления и алгебраические выражения
1.
8. Числа, вычисления иалгебраические
выражения
2.
• Вычисления3. Свойства степени
• Произведение степеней• Частное степеней
• Степень степени
• Степень произведения
• Степень дроби
4. Произведение степеней
• При умноженииЕсли а- число,
ст епеней с
отличное от
одинаковыми
нуля, а m, п –
основаниями
целые числа, то
показат ели
складывают ся
а а а
т
п
т п
5. Примеры:
2х х х
3
1 2 3
х
х
4
1 1 5
1 4
( ) ( )
3 3
3
15
7
22
2,4 а а 2,4а
6. Частное степеней
Если а – число,не равное 0, и
m, п- целые
числа, то
т
При делении ст епеней
с одинаковыми
основаниями из
показат еля делимого
вычит ают показат ель
делит еля
а
т п
а
п
а
7. Примеры:
63
у :у у
14
6 ( 3 )
у
3
х
14 14
28
х
х
14
х
9
9 1
8
( 7 ) : ( 7 ) ( 7 ) ( 7 )
8. Степень степени
Если а – число, неравное нулю и m,
п – целые числа,
то
При возведении
ст епени в ст епень
показат ели
перемножают ся
(а ) а
т п
т п
9. Примеры:
5 2(f ) f
5 ( 2 )
f
10
1
1
1
3 4
3 ( 4 )
12
(( 2 ))
2
2
10. Степень произведения
• Если а, b – числа, При возведении вст епень произведения
не равные нулю и
возводят в эт у ст епень
n – любое целое
каждый множит ель и
число, то
результ ат ы
перемножают
(а b) а b
п
п
п
11. Примеры:
88
(c d ) c d
4
8
4
(0,3 v) 0,3 v
3
4
3
3
( x r l ) ( x) r l
3
12. Степень дроби
Если a, b – числа,причем a, b 0, и
n - любое целое
число, то
При возведении дроби
в ст епень возводят в
эт у ст епень
от дельно ее
числит ель и
знаменат ель
п
а п
а
( ) п
b
b
13.
14.
15. Задание: проверьте, верны ли данные равенства и ответьте на вопрос «почему?»
16 = 4;81 = 9;
8 = 3;
9 = 3;
0 = 0;
25 = 5.
16.
Если а ≥ 0, b ≥ 0, то a b a b64 0,04 64 0,04 8 0,2 1,6
Решите самостоятельно
36 0,25 36 0,25 6 0,5 3
121 0,49 121 0,49 11 0,7 7,7
9 64 0,25 9 64 0,25 3 8 0,5 12
0,36 144 2,25 0,36 144 2,25 0,6 12 1,5 10,8
17.
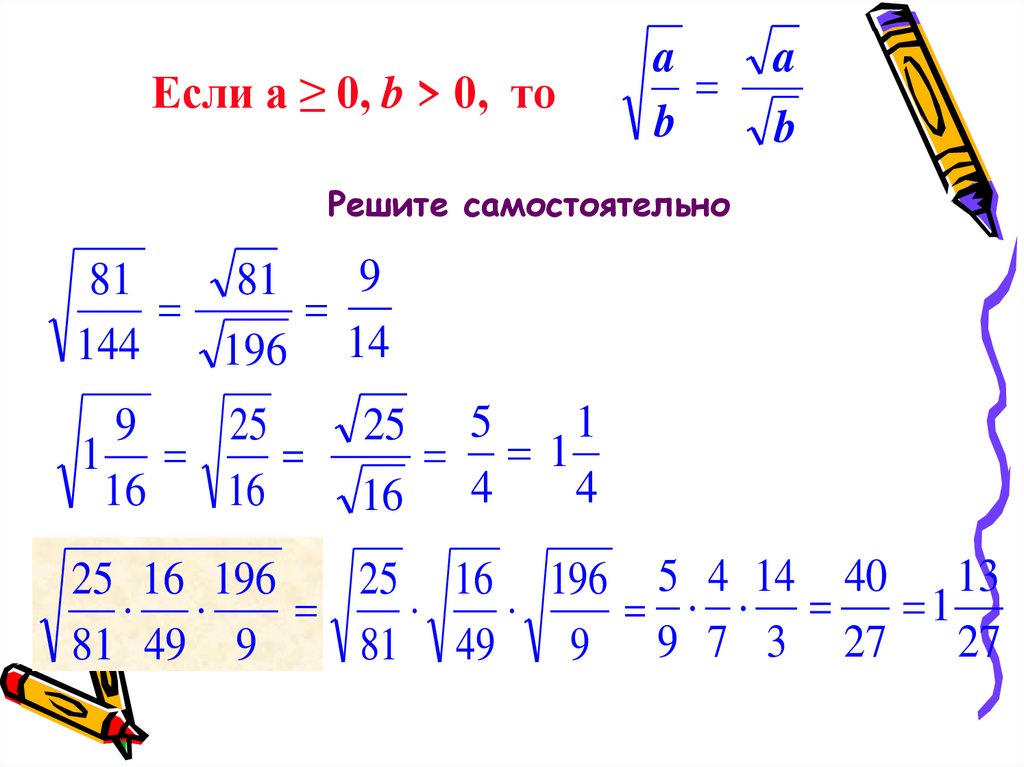
Если а ≥ 0, b > 0, тоa
b
a
b
Решите самостоятельно
9
81
81
144
196 14
9
25
1
16
16
1
5
1
4
16 4
25
25 16 196
25 16 196 5 4 14 40 13
1
27
81 49 9
81 49
9 9 7 3 27
18. Карточка – памятка «Свойства арифметического квадратного корня».
ab
a
b
1
a
a
2 b
b
3
a2 a
4
a 2b a b
a 0,b 0
a 0,b 0
a 0,b 0
19. Вычислите:
20.
04.02.202420
21.
22.
23.
• Целые алгебраическиевыражения
24. Формулы сокращенного умножения (а + b)²= а²+2аb+b² (а - b)²= а²-2аb+b² а² - b² = (а-b) (а+b) а³ + b³ = (а+b) (а²-аb+b²) а³-
Формулы сокращенногоумножения
(а + b)²= а²+2аb+b²
(а - b)²= а²-2аb+b²
а² - b² = (а-b) (а+b)
а³ + b³ = (а+b) (а²-аb+b²)
а³- b³ = (а-b) (а²+аb+b²)
(а + b)³= а³+3а²b+3аb²+b³
(а - b)³= а³-3а²b+3аb²-b³
25.
26.
• Рациональныеалгебраические выражения
27.
Методразложения на
множители
Вынесение
общего
множителя за
скобки
Формулы
сокращённого
умножения
Способ
группировки
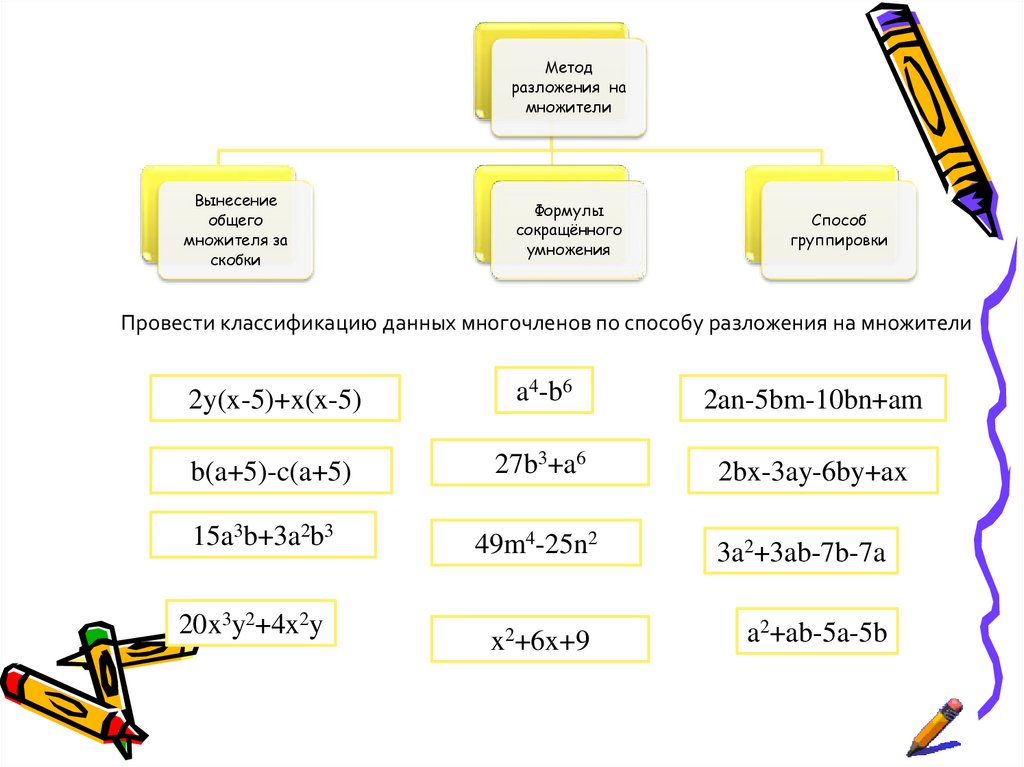
Провести классификацию данных многочленов по способу разложения на множители
2y(x-5)+x(x-5)
a4-b6
2an-5bm-10bn+am
b(a+5)-c(a+5)
27b3+a6
2bx-3ay-6by+ax
15a3b+3a2b3
49m4-25n2
3a2+3ab-7b-7a
x2+6x+9
a2+ab-5a-5b
20x3y2+4x2y




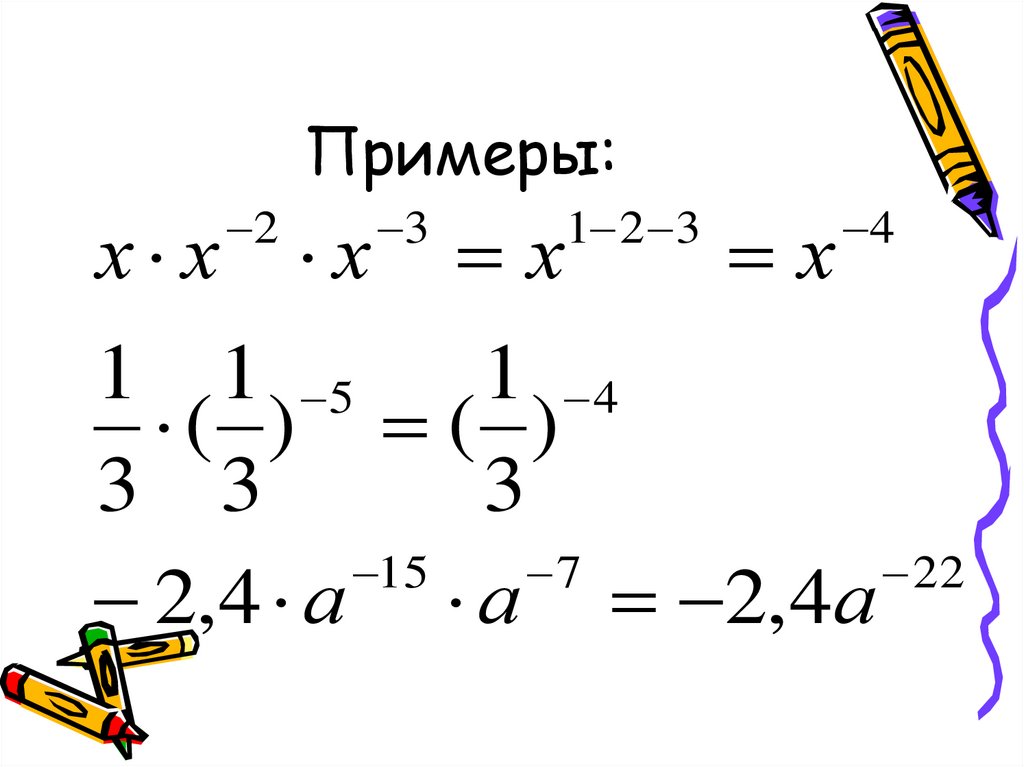

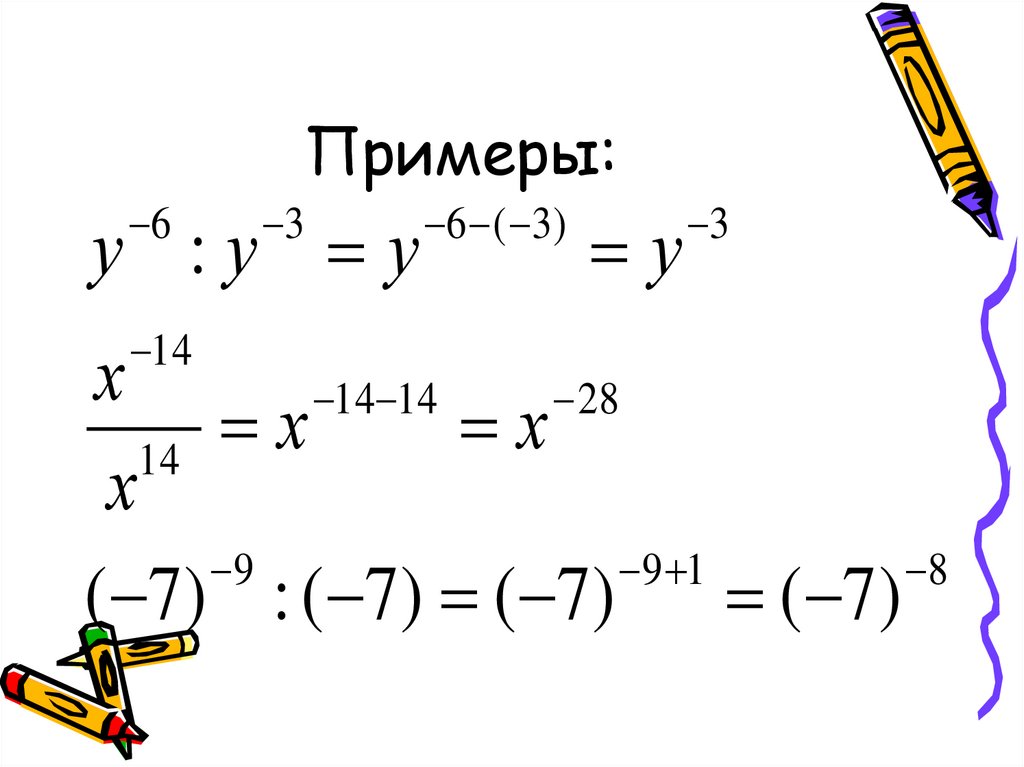

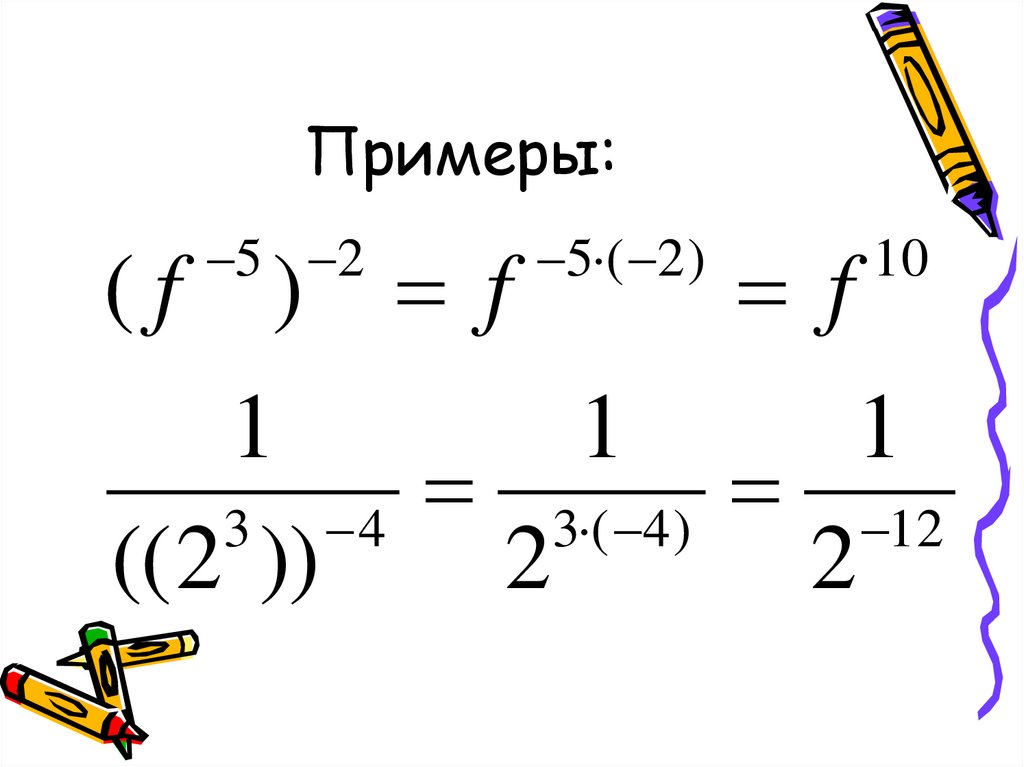

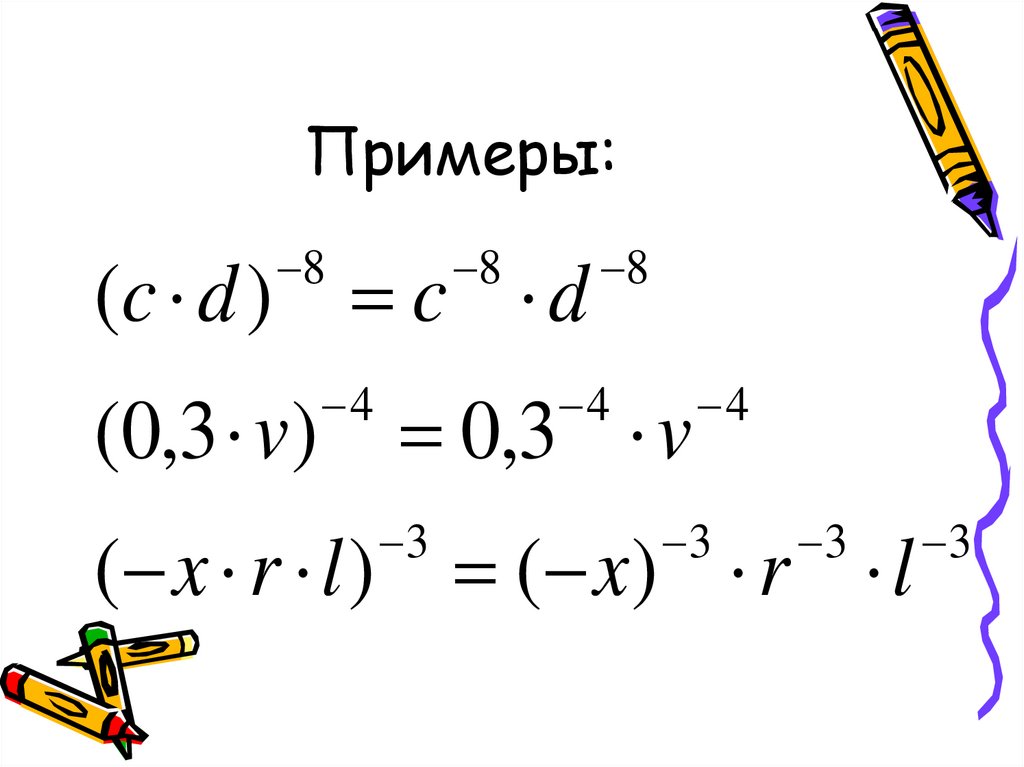


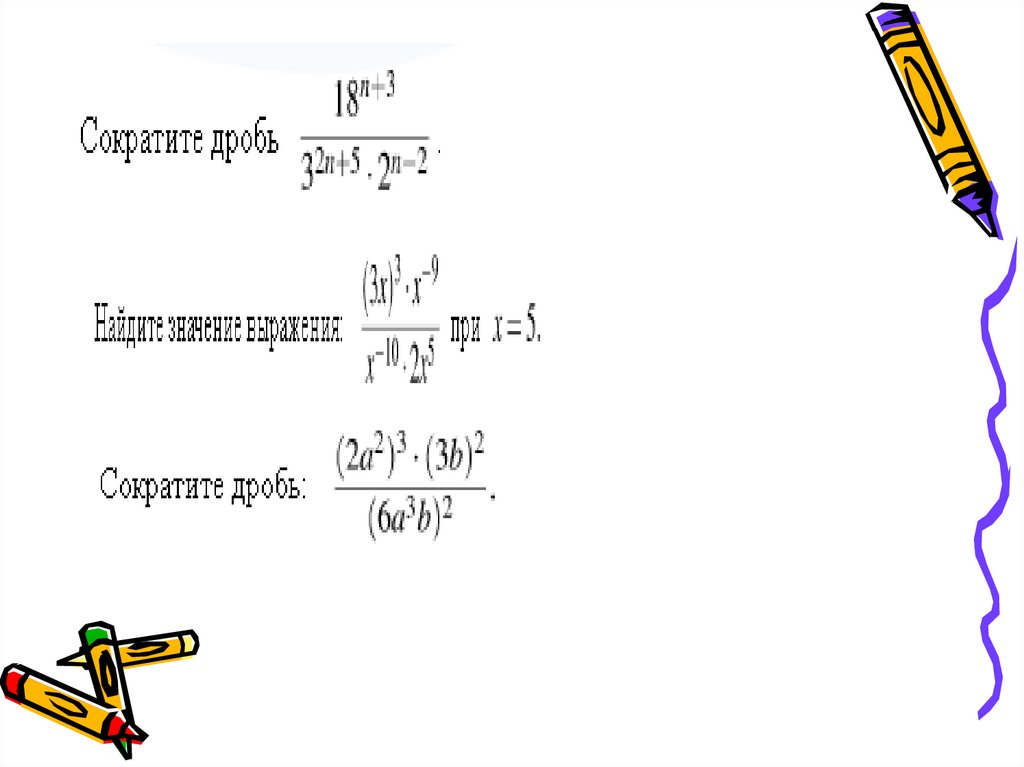











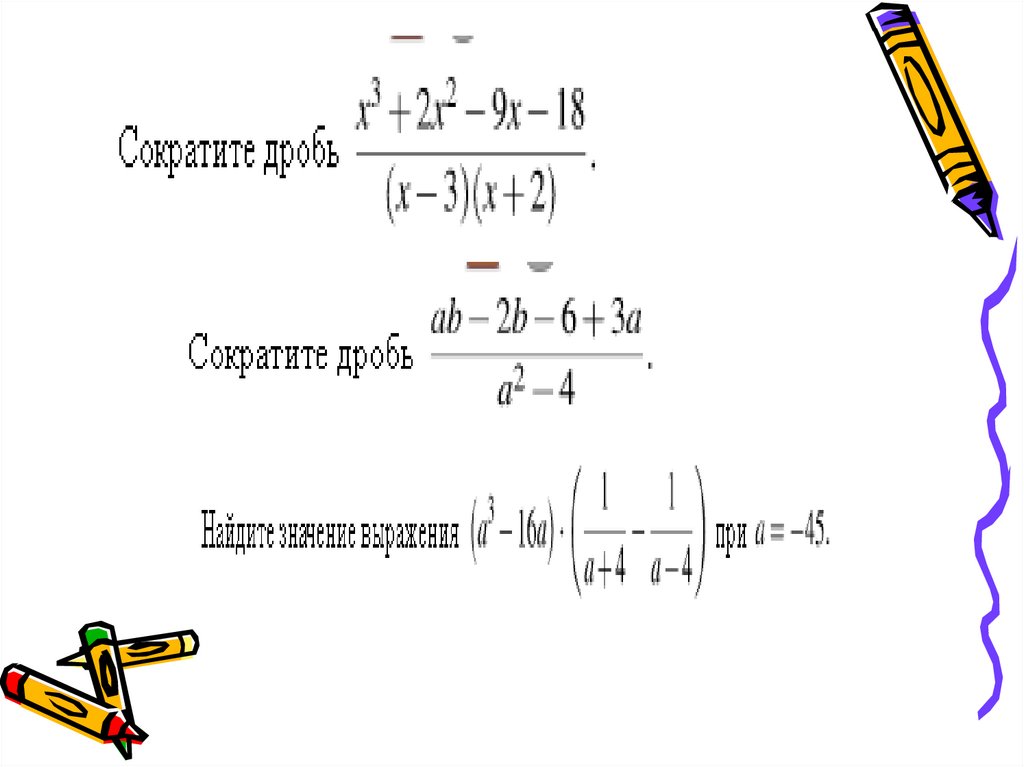
 Математика
Математика








