Физика. Механика

1. ФИЗИКА

МЕХАНИКА
Лектор: к.т.н., доцент кафедры «Физика»
Веретимус Надежда Константиновна
Лекции Веретимус Н.К. и Веретимус Д.К.

2. Литература по курсу (1 модуль)

1. Иродов И.Е. Механика. Основные законы.
– М. – С.-П.: Физматлит, 2000.
2. Иродов
И.Е.
Волновые
процессы.
Основные законы. – М. – С.-П.:
Физматлит, 1999.
3. Савельев И.В. Курс общей физики. Том 1.
– М.: Наука, 1978 – 1986.
4. Савельев И.В. Курс общей физики. Том 2.
– М.: Наука, 1978 – 1986.

3.

5. Глаголев К.В., Морозов А.Н. Физическая
термодинамика: Учеб. пособие. – М.: Издво МГТУ им. Н.Э.Баумана, 2004. – 368
с./Под
ред.
Л.К.Мартинсона,
А.Н.Морозова.
6. Иродов И.Е. Физика макросистем.
Основные законы. – М. – С.-П.:
Физматлит, 2001.
7. Иродов И.Е. Задачи по общей физике. –
М.: Бином, 1998 – 2001

4.

Физические
основы
механики.
Колебания и волны. Элементы специальной
теории
относительности:
учебное
пособие/Д.К.Веретимус, Н.К.Веретимус; под
ред. А.Н.Морозова. – Москва: Издательство
МГТУ им. Н.Э.Баумана. 2018 - 135 с. Издание
доступно
в
электронном
виде
по
адресу: http://ebooks.bmstu.press/catalog/70/bo
ok1854.html

5.

Физические
основы
механики.
Колебания и волны. Элементы специальной
теории относительности. Модуль 1: учебное
пособие /Д.К. Веретимус, Н.К. Веретимус;
под ред. А.Н. Морозова. 2-е изд., испр. и доп.
– Москва: Издательство МГТУ им. Н.Э.
Баумана. 2022 – 163 с. Издание доступно в
электронном
виде
по
адресу:
https://bmstu.press/catalog/item/7765/

6.

Основы физической термодинамики.
Модуль 2: учебное пособие / Д.К. Веретимус,
Н.К. Веретимус; под ред. А.Н. Морозова –
Москва:
Издательство
МГТУ
им.
Н.Э.Баумана, 2021. – 140 с. Издание доступно
в
электронном
виде
по
адресу:
https://bmstu.press/catalog/item/7177/

7.

Физика – наука, изучающая простейшие
и
вместе
с
тем
наиболее
общие
закономерности явлений природы, свойства и
строение материи и законы ее движения.
Понятия физики и ее законы лежат в основе
всего естествознания. Физика – точная наука
и изучает количественные закономерности
явлений.
Закон – необходимое, существенное,
устойчивое,
повторяющееся
отношение
между явлениями в природе.

8.

Явление – то или иное обнаружение
предмета,
внешние
формы
его
существования.
В физике – два равноправных метода
исследований: экспериментальный (дает
основания для построения гипотез, теорий) и
теоретический (позволяет предварительно
создать гипотезу, теорию, а затем обязательно
подтвердить экспериментально).
Механика – наука о механическом
движении материи в пространстве и во
времени.

9.

Механическое движение – изменение
положения одних тел или частей тела
относительно других.
Материальная точка (МТ) – тело,
размерами и формой которого в условиях
данной задачи можно пренебречь.
Твердое тело (абсолютно твердое
тело) – система МТ, расстояния между
которыми не меняются.
Траектория – геометрическое место
точек пространства, в которых точка
последовательно побывала за время своего
движения.

10.

Тело (точка) отсчета – твердое тело
(точка), которое служит для определения
положения интересующего нас тела. Система
отсчета (СО) = тело отсчета + связанные с
ним система координат и часы.
В классической механике изменение
времени происходит одинаково во всех СО,
независимо от характера их движения.
Рассматриваем
движение
МТ
в
трехмерном евклидовом пространстве (для
него правомерны все аксиомы и теоремы
геометрии Евклида).

11.

Основные виды движения твердого
тела:
1. Поступательное движение – прямая,
соединяющая любые две точки тела,
перемещается, оставаясь параллельной
своему начальному положению.
2. Вращательное движение – все точки
тела, лежащие на оси вращения, остаются
неподвижными, траектории остальных
точек – окружности (дуги окружностей).

12. Лекция № 1

КИНЕМАТИКА
Лекции Веретимус Н.К. и Веретимус Д.К.

13.

Кинематика – раздел механики, в
котором движение тел и сплошных сред
рассматривается без выяснения причин,
вызвавших это движение.
Размерности кинематических величин
определяются размерностями длины и
времени.
Способы описания движения точки:
векторный;
координатный
и
естественный.

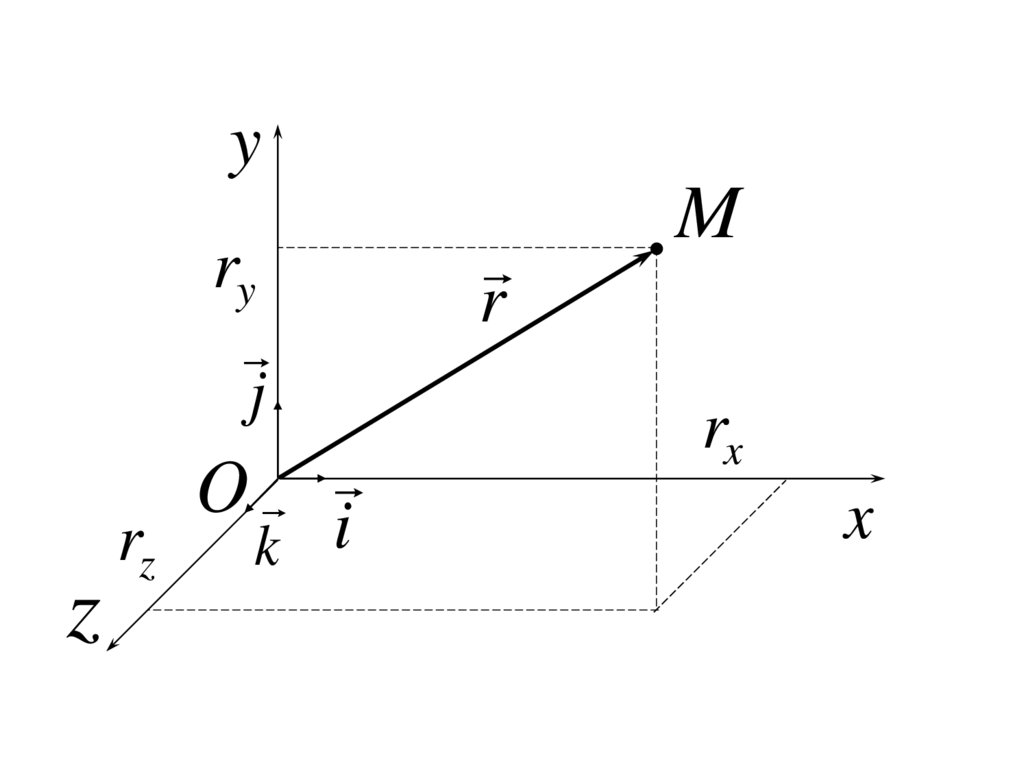
14. Кинематика МТ

Положение движущейся т. M относительно
неподвижной т. O (начала отсчета) в каждый
момент времени определяет
радиус-вектор r .
M
Уравнение движения в
r
векторной форме
O
r r t , (1.1)
t – время.

15.

Координатный
способ
задания
движения, в проекциях на оси прямоугольной
декартовой системы координат
r t rx t i ry t j rz t k ,
(1.2)
где i , j , k – единичные орты осей x, y и z
соответственно и

16.

y
ry
j
z
rz
O i
k
r
M
rx
x

17.

rx t x t , ry t y t , rz t z t
2
2
2
r r rx ry rz
s t
an
R
O
(1.3)
M a
a
Путь s = s(t) –
расстояние,
пройденное точкой
вдоль траектории за
время t.

18. Средняя скорость МТ при векторном задании движения

r
(1.4)
,
t
где r r2 r1 – вектор перемещения МТ
за время Δt,
Δt= t2 – t1
r1 r t1
r2 r t2
Мгновенная скорость МТ
При векторном способе задания движения
dr
dt
(1.5)

19.

При координатном способе
xi y j z k
(1.6)
dz
z
dt
(1.7)
2
2
2
x y z
(1.8)
dy
dx
,
x
, y
dt
dt
d s dt ,
или
t
(1.9)
где s s t d t
– путь, пройденный МТ
0
за время t (см. рис. на слайде 18).

20. Ускорение МТ

При векторном способе задания движения
2
d d r
2
a
(1.10)
dt
dt
При координатном способе
a axi a y j az k
d y
d x
d z
, ay
,
где a x
, az
dt
dt
dt
2
2
2
a a ax a y az
(1.11)
(1.12)
(1.13)

21.

Криволинейное движение
плоскости. При естественном
описания движения скорость МТ
,
МТ в
способе
(1.14)
s t
d s d t – проекция
где
на
направление
единичного вектора
n
R
O
M

22.

Продифференцируем (1.14) по времени.
Ускорение МТ
d
d d
a
dt
dt dt
d
d ds
2 d
dt
ds d t
ds
d
2 d
a
dt
ds
(1.15)

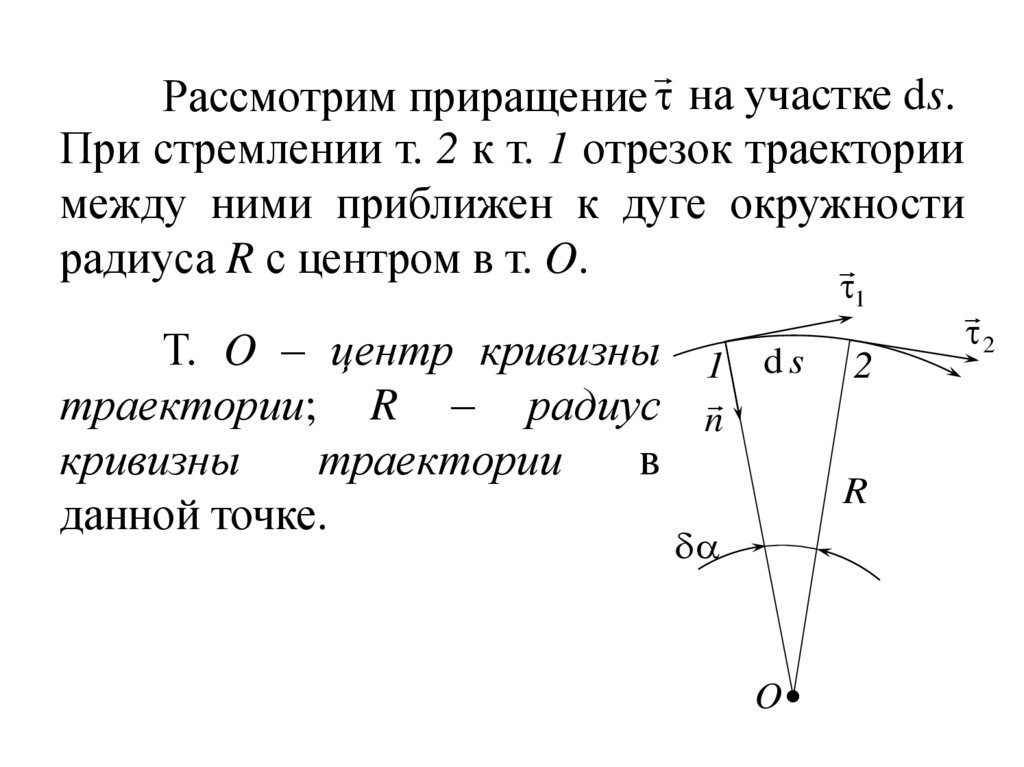
23.

Рассмотрим приращение на участке ds.
При стремлении т. 2 к т. 1 отрезок траектории
между ними приближен к дуге окружности
радиуса R с центром в т. O.
1
Т. O – центр кривизны 1 d s 2
траектории; R – радиус n
кривизны
траектории
в
R
данной точке.
O
2

24.

Из рис., при d s 0, d и малых
углах δα
1
ds
d
d
R
2
d 1
1
ds R
Если ввести единичный вектор нормали к
траектории в т. 1, направленный к центру
кривизны, то
d n
ds R
(1.16)

25.

d
(1.16) → (1.15) a
n
dt
R
При криволинейном движении точки полное
ускорение
a an a ,
(1.17)
2
d
an n
где
a
(1.18)
;
R
d
t
2
a
an
– тангенциальное и нормальное ускорения
соответственно.
2
2
a a an a
(1.19)

26. Вращение твердого тела относительно неподвижной оси

Кинематическое
уравнение
при
вращательном движении: φ = φ(t), где φ – угол
поворота относительно оси вращения z.
Вектор угловой скорости точки тв. тела
d
dt

27.

где d – псевдовектор (вектор, направление
которого связано с направлением вращения).
z
d
d
R
r
O
d s
dr
R – радиус траектории,
– мгновенная скорость
точки тв. тела.

28.

Вектор углового ускорения тв. тела
2
d d
2
dt
dt
Проекции на ось z:
d z
z
dt
(1.20)
z d z d z
dt
dt2
2
(1.21)

29. Связь угловых и линейных характеристик:

• приращения угла dφ и дуги ds
d s Rd
(1.22)
• скорости и угловой скорости
,r ,
R
(1.23)
• тангенциального и углового ускорений
a z R
(1.24)
• нормального ускорения и угловой скорости
an R
2
(1.25)

30. Равноускоренное движение

• При a const
в векторной форме
Из (1.10)
d a dt
t
0
0
d a dt
t
0 a d t
0 at
0

31.

Из (1.5)
r
t
d r d t
r0
d r d t
0
t
r r0 0 at d t
0
t
t
0
0
r r0 0 d t at d t
2
at
r r0 0t
2

32.

Аналогично получают зависимости угловой
скорости и угла поворота от времени при
равноускоренном вращательном движении.

33. В случае равноускоренного движения

• При a const
в векторной форме
0 at
2
at
r r0 0t
2
в координатной форме
(1.26)
x 0 x a x t ,
x x0 0 xt a xt 2 2,
y 0 y a yt ,
y y0 0 yt a yt 2 2, (1.27)
z 0 z a z t ,
z z0 0 z t az t 2.
2

34.

• При
z const
z 0 z z t
zt
z 0 z 0 z t
2
2
(1.28)
где r0 , 0 , 0 z , 0 z – соответственно радиус-
вектор, скорость, угловое перемещение и
угловая скорость в начальный момент
времени (при t = 0), а x0, y0, z0 и υ0x, υ0y, υ0z –
начальные координаты и проекции начальной
скорости соответственно.

35. Классический закон сложения скоростей и ускорений при поступательном движении подвижной K-СО относительно K-СО

Классический закон сложения
скоростей и ускорений при
поступательном движении
подвижной K -СО относительно
K-СО
В K-СО начало координат K -СО
характеризуется радиус-вектором r0 , а ее
скорость и ускорение – векторами 0 и a 0
соответственно.

36.

y
y
K
K
Положение т.
М в K-системе
r
r
r r0 r (1.29)
r0
M
O
x
z
O
z
d r d r0 d r
dt dt
dt
x

37.

Формула преобразования скорости в
классической механике (из (1.5) и (1.29))
(1.30)
0
формула преобразования ускорения (из
(1.10) и (1.30))
d d 0 d
dt
dt
dt
a a0 a
(1.31)
где и a – скорость и ускорение т. M в K
СО;
и a – соответственно скорость
и ускорение т. M в K -СО.

38.

В СИ
S=[м]
φ=[рад]
t =[с]
υ=[м/с]
ω=[рад/с]
a =[м/с2]
ε =[рад/с2]