Теорема косинусов и теорема синусов. Решение задач ОГЭ с помощью теоремы синусов и теоремы косинусов

1.

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 12
МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ ГОРОД-КУРОРТ АНАПА
ИМЕНИ КАВАЛЕРА ОРДЕНА МУЖЕСТВА АЛЕКСАНДРА КАШИРИНА
Индивидуальный итоговый проект
ТЕМА:
«Теорема косинусов и теорема синусов.
Решение задач ОГЭ с помощью
теоремы синусов и теоремы косинусов»
Выполнила:
Косинова Валерия Романовна
ученица 9 «Г» класса;
куратор проекта:
Иконникова Яна Васильевна
учитель(проектная деятельность)
г.-к. Анапа 2023 г.

2.

Цель работы выявить насколько важны
теоремы косинусов и теорема синусов в
заданиях по математике и расширить знания
о них.
Задачи:
Изучить теорему косинусов и теорему синусов
Научиться использовать теоремы на практике
задач ОГЭ
Гипотеза исследования:можно
предположить, что теоремы синусов и
косинусов широко используются в заданиях
ОГЭ второй части.

3.

Актуальность: для проекта я выбрала тему теорему
синусов и теорему косинусов,потому что посчитала ее
интересной и актуальной в задачах 2 части экзамена.
Также я заметила, что раздел тригонометрия вызывает
сложности в понимании у ребят, поэтому я решила
рассмотреть данные темы как можно подробно.
Предмет исследования: теорема синусов и теорема
косинусов
Объект исследования: задачи математики, при решении
которых нужны теорема синусов и теорема косинусов
Методика исследования: анализ информации в
Интернете.

4.

Теорема синусов и теорема
косинусов – теоремы
одного из разделов
математики, в котором
изучаются
тригонометрические
функции и их
использование в
геометрии.
Раздел под названием
тригонометрия появился
очень давно астрономами,
для ориентирования по
звездам и планетам

5.

Теорема косинусов - квадрат стороны треугольника
равен сумме квадратов двух других сторон минус
удвоенное произведение этих сторон на косинус
угла между ними.
a2 = b2 + c2 – 2 × b× c × cosA.
В начале 19 века теорема стала записываться в
виде алгебраической записи.

6.

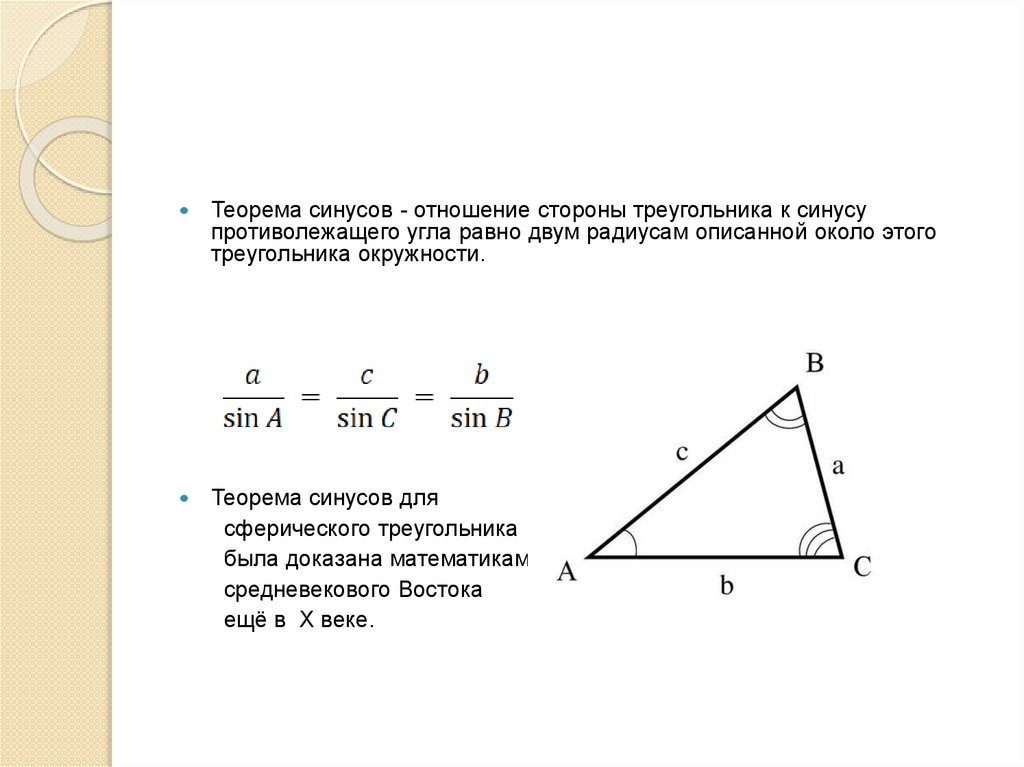
Теорема синусов - отношение стороны треугольника к синусу
противолежащего угла равно двум радиусам описанной около этого
треугольника окружности.
Теорема синусов для
сферического треугольника
была доказана математиками
средневекового Востока
ещё в Х веке.

7.

Решение задачи ОГЭ с помощью
теоремы косинусов и теоремы
синусов
Точки M и N лежат на стороне AC треугольника ABC на
расстояниях соответственно 9 и 11 от вершины A. Найдите
радиус окружности,
проходящей через точки M и N и касающейся луча AB, если
cosBAC =
Дано:
M € AC; N € AC; AM = 9; cosBAC =
AN = 11.
Найти:
R.
Решение:

8.

1) Касательная и секущая проведены к окружности из одной точки
( по свойству касательной и секущей)
2)Рассмотрю треугольник AEM, для нахождения EM применяю теорему
косинусов:
3) Рассмотрю треугольник AEN, для нахождения EN также применяю теорему
косинусов:
Тогда (сюдя из 2 действия)

9.

4) т.к AE = EN, следовательно треугольник AEN–равнобедренный,
( тогда по свойству равнобедренного треугольника), углы при
основаниях равны-EAN = ENA .
Для нахождения радиуса описанной окружности, мне необходимо
значение синус угла ENA .
Найти синус этого угла можно с помощью основного
тригонометрического тождества:
5)Рассмотрю треугольник и найду искомый радиус через синус.
Радиус, окружности, описанной около треугольника, равен
отношению стороны треугольника EMк удвоенному синусу
противолежащего угла-EN
Ответ: 5,4

10.

Спасибо за внимание!