Осесимметричная задача теории упругости

1.

Занятие 3
ОСЕСИМ М ЕТРИЧНАЯ ЗАДАЧА
ТЕОРИИ У ПРУ ГОСТИ

2.

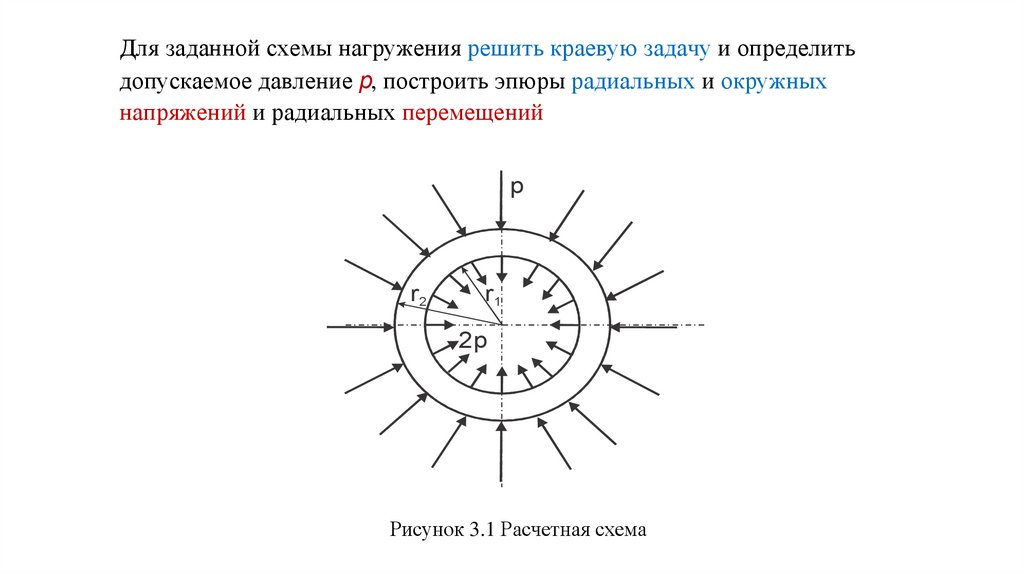
Для заданной схемы нагружения решить краевую задачу и определить
допускаемое давление p, построить эпюры радиальных и окружных
напряжений и радиальных перемещений
p
r2
r1
2p
Рисунок 3.1 Расчетная схема

3.

Исходные данные:
r1 := 0.04 cì
r2 := 0.12 cì
s äîï
:= 180 ×10
6
Ïà
Êðèòåðèé Ñåí - Âåíàíà
E := 2 ×10
11
Ïà
n := 0.3
Решение:
Приведем уравнения равновесия в напряжениях и перемещениях для
осесимметричной задачи теории упругости.
Уравнение равновесия в напряжениях:
d
sr +
dr
sr - sq
r
0

4.

Уравнение равновесия в перемещениях:
2
1 ×d × u
d
u + ×× u × 2
r ×dr × 2
dr
r
0
sr
×d
u×
×× u + n × ×
2
r×
1 - n ×dr
sq
×u
d ×
×× + n × u ×
2 r
dr ×
1-n ×
E
E

5.

Запишем общее решение в перемещениях:
u( r)
1
C1 ×r + C2 ×
r
Запишем общее решение в напряжениях:
E ×
1- n×
(
)
sr
××C1 × 1 + n - C2 ×
2
2 ×
1-n ×
r ×
1-n×
× (
sq
××C1 × 1 + n ) + C2 ×
2
2 ×
1-n ×
r ×
где С1 и С2 константы интегрирования
E

6.

Запишем граничные условия для данной системы (рисунок 3.1):
1) r=r1
sr
2p
2) r=r2
sr
-p
Решим краевую задачу:
Ñ1 := 1
Given
E
×
C2 := 1
1-n×
××C1 ×( 1 + n ) - C2 ×
2
1-n ×
×
E
×
1-n×
××C1 ×( 1 + n ) - C2 ×
2
1-n ×
×
× 2p
2
r1 ×
×
× -p
2
r2 ×
×
×-4.81e-12 ×p ×
Find( C1 , C2) float, 3 ® ×
×
×-3.51e-14 ×p ×

7.

В результате численного решения константы интегрирования равны:
C1 ( p) := -4.81e-12 ×p
C2 ( p) := -3.51e-14 ×p
Тогда выражения для напряжений и перемещений имеют вид:
1
u( r , p) := C 1 ( p) ×r + C 2 ( p) ×
r
1-n×
×
(
)
s r ( r , p) :=
××C 1 ( p) × 1 + n - C 2 ( p) ×
2
2 ×
1-n ×
r ×
E
1-n×
×
(
)
s q ( r , p) :=
××C 1 ( p) × 1 + n + C2 ( p) ×
2
2 ×
1-n ×
r ×
E

8.

Определим значение допускаемого давления p по заданному
критерию Сен-Венана
s ýêâ
s 1 - s 3 × s äîï
Найдем эквивалентные напряжения в точках r=r1 и r=r2
Ïðè
r1
s r r1 , p float, 3 ® 2.0 ×p
(
)
s z := 0
sq
r
ò. ê. öèëèíäð îòêðûòûé
( r1 , p) float, 3 ® -4.75 ×p
s ýêâr1 ( p) := 2.0 ×p -
( -4.75 ×p) float, 3 ® 6.75 ×p

9.

Ïðè
r2
s r r2 , p float, 2 ® -1.0 ×p
(
)
s z := 0
sq
r
ò. ê. öèëèíäð îòêðûòûé
( r2 , p) float, 3 ® -1.75 ×p
s ýêâr2 ( p) := 0 -
( -1.75 ×p) float, 3 ® 1.75 ×p
Опасное сечение при r=r1
Тогда эквивалентное напряжение равно:
s ýêâ_ÑÂ( p) := s ýêâr1 ( p)
s ýêâ_ÑÂ( p) = 6.75 ×p

10.

Запишем условие прочности:
s ýêâ_ÑÂ( p) × s äîï
Получим, что допускаемая нагрузка равна:
6.75 ×p × s äîï
päîï ×
s äîï
päîï :=
s äîï
7
= 2.667 × 10
ÌÏà
6.75
6.75
Построим эпюры при найденном значении допускаемой нагрузки
p := päîï
Для построения эпюр введем новую переменную
r_gr := 0 ,
1
1500
.. r2

11.

r_gr := 0 ,
1
.. r
1500 2
7
6×10
7
4.875×10
7
3.75×10
7
2.625×10
s r ( r_gr , p)
7
1.5×10
6
3.75×10
6
- 7.5×10
7
- 1.875×10
7
- 3×10
0.04
0.05
0.06
0.07
0.08
0.09
0.1
0.11
0.12
r_gr
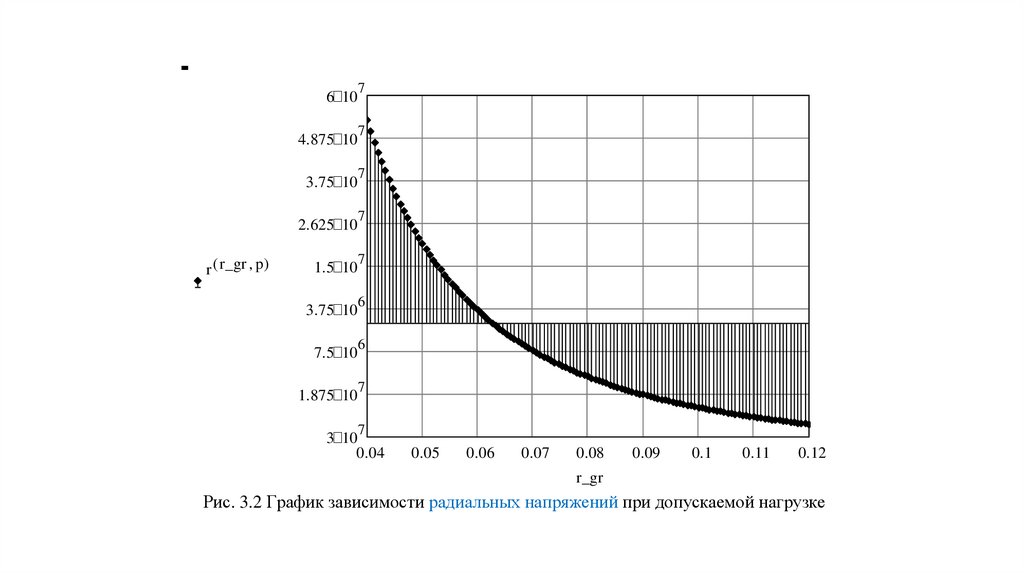
Рис. 3.2 График зависимости радиальных напряжений при допускаемой нагрузке

12.

0
7
- 1.875×10
7
- 3.75×10
7
- 5.625×10
s q ( r_gr , p)
7
- 7.5×10
7
- 9.375×10
8
- 1.125×10
8
- 1.313×10
8
- 1.5×10
0.04
0.05
0.06
0.07
0.08
0.09
0.1
0.11
0.12
r_gr
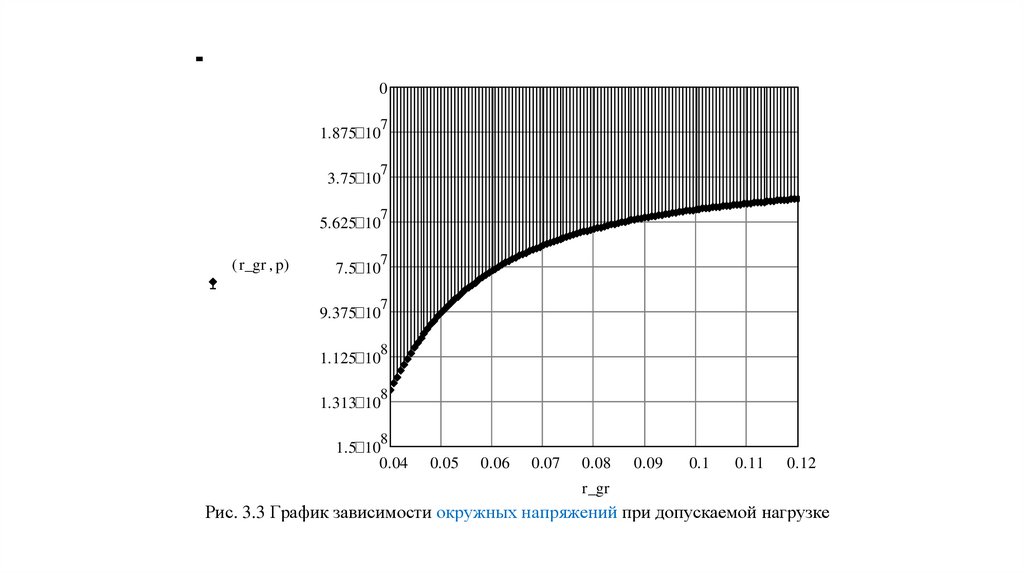
Рис. 3.3 График зависимости окружных напряжений при допускаемой нагрузке

13.

-6
6×10
-6
1.5×10
-6
- 3×10
-6
- 7.5×10
u ( r_gr , p)
-5
- 1.2×10
-5
- 1.65×10
-5
- 2.1×10
-5
- 2.55×10
-5
- 3×10
0.04
0.05
0.06
0.07
0.08
0.09
0.1
0.11
0.12
r_gr
Рис. 3.4 График зависимости радиальных перемещений при допускаемой нагрузке

14.

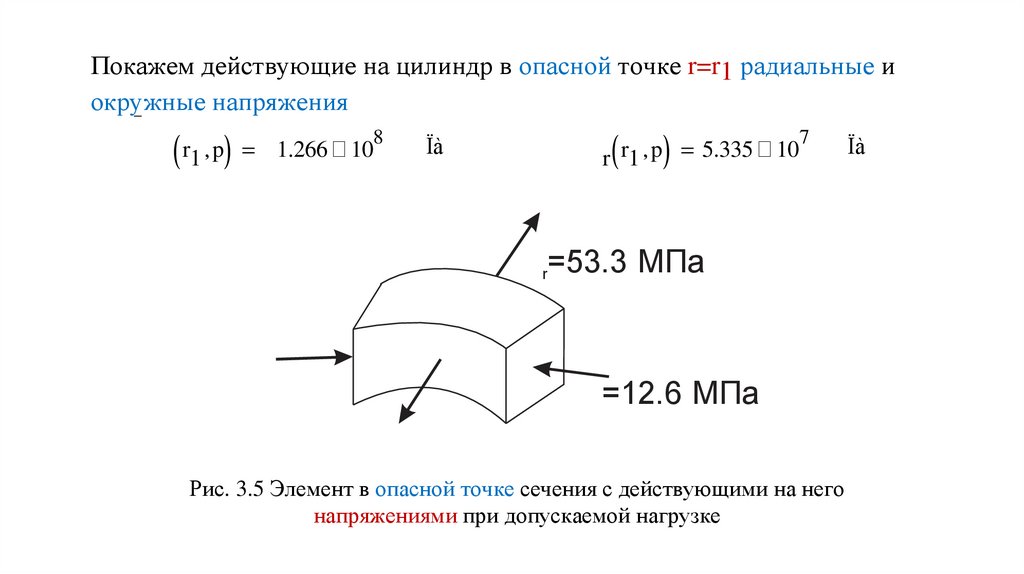
Покажем действующие на цилиндр в опасной точке r=r1 радиальные и
окружные напряжения
sq
(
)
8
r1 , p = -1.266 × 10
Ïà
(
)
s r r1 , p
7
= 5.335 × 10
sr=53.3 МПа
sq=12.6 МПа
Рис. 3.5 Элемент в опасной точке сечения с действующими на него
напряжениями при допускаемой нагрузке
Ïà