Похожие презентации:
Логарифмические уравнения. Решение логарифмических уравнений
1.
Решениелогарифмических
уравнений
2.
Свойства логарифмовloga 1= 0 loga а= 1
loga( ху)= loga х+loga у
х log х− log у
loga =
a
a
у
n
loga b = nloga b
logan b=
1
loga b
n
loga b=
logc b
logc a
3.
Этапы решения логарифмического уравнения:1. Найти область допустимых значений (ОДЗ)
переменной;
2. Решить уравнение, выбрав метод решения;
3. Проверить найденные корни непосредственной
подстановкой в исходное уравнение или выяснить,
удовлетворяют ли они условиям ОДЗ.
4.
Простейшее логарифмическоеуравнение решается через
определение логарифма:
log a x b x a , x>0
b
Например:
log 3 x 2
одз : x 0
x 3
2
x 9 ; 9 одз
Ответ: x= 9
5.
№1. Решить уравненияa ) log 2 x 1 3
log 2 x 1 log 2 2
x+1= 8
x= 7; 7 одз
3
одз :
x 1 0
x 1
Ответ: x= 7
В данном примере число 3 представили в виде логарифма:
log 2 8 = 3, т. к. 23 = 8
Если в левой и правой части получили логарифм с одним
основанием, логарифм убираем и приравниваем друг к другу
выражения, стоящие под знаком логарифма.
6.
б ) log 2 x 1 log 2 x 3 3x 1 0
x 1
одз :
x 1
x 3 0
x 3
log 2 x 1 x 3 log 2 23
x2 4x 3 8
x2 4x 5 0
1 одз
x 2 5 ; 5 одз
x 1 1;
Ответ : 1
7.
в ) lg x 3 2 lg 2 lg xx 3 0
x 3
одз :
x 0
x 0
x 0
lg x 3 lg x lg 2 2
Согласно свойству:
nloga b= loga bn
lg x x 3 lg 4
x2 3x 4
x2 3x 4 0
x1 1; 1 одз
x 2 4 ; 4 одз
Ответ : 1
8.
г ) log 7 36 log 7 3 x 12 log 7 4log 7 3 x 12 log 7 36 log 7 4
36
log 7 3 x 12 log 7
4
3 x 12 9
3 x 21
x 7 ; 7 одз
Ответ : 7
одз :
3 x 12 0
3 x 12
x 4
9.
Решение уравнения под буквой д(метод замены перменной)
д) log x log 4 x 1,5 0
2
4
одз : x 0
1
2
log 4 x log 4 x 1,5 0
log 4 x 1
2
Обозначим : log 4 x t x 4 ; 4 одз
t 2 0 ,5 t 1,5 0
t1 1
t 2 1,5
Ответ : 0 ,125 ; 4
log 4 x 1,5
x 4 1, 5
1
x 3
42
1
x
43
1
1
одз
x ;
8
8
10.
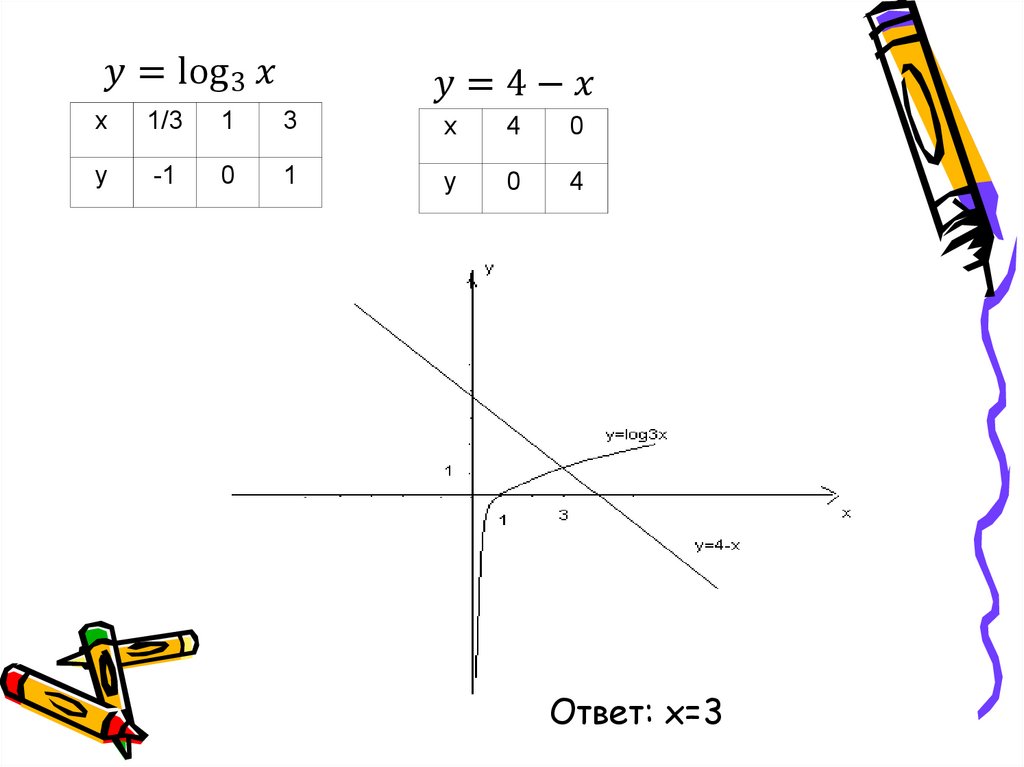
Графический способ решения.Найдите корни уравнения
loq x= 4− x
3
1. Построить графики функций;
2. Выделить точки пересечения графиков функций.







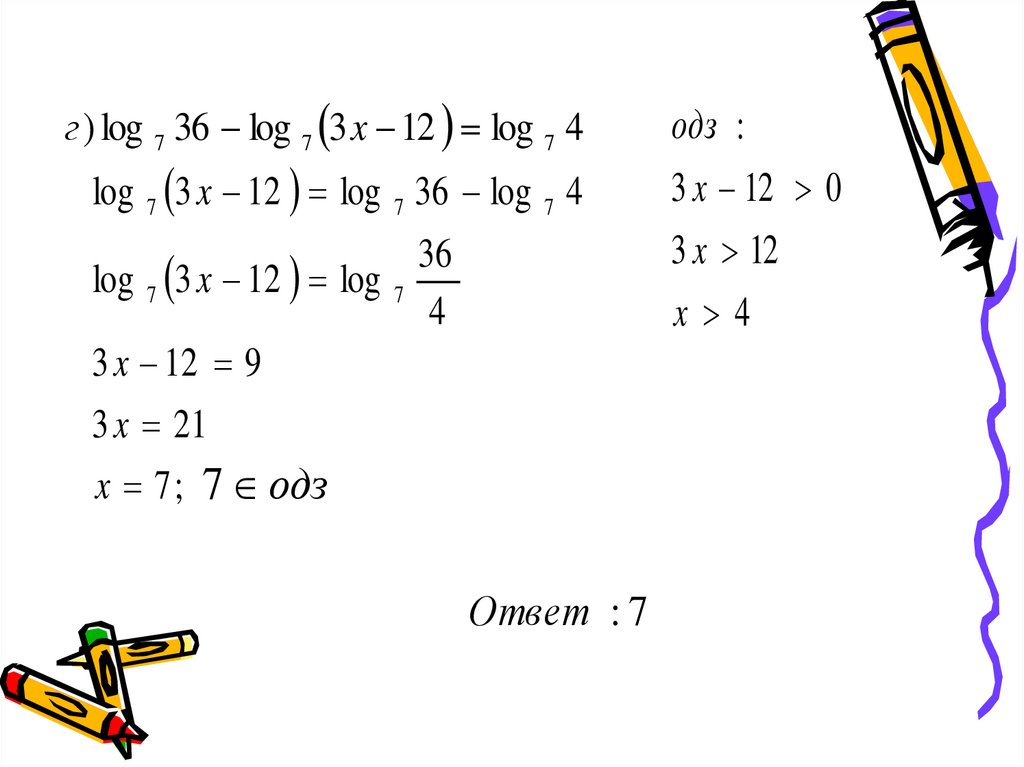







 Математика
Математика








