Спектры периодических сигналов

1.

2.

3.

Спектры периодических сигналов;
Спектры Т-финитных сигналов;
Свойства преобразования Фурье. Равенство Парсеваля.
Основная литература
1.
Андреев Р.Н., Краснов Р.П., Чепелев М.Ю. Теория электрической связи: курс лекций. Учебное
пособие для вузов. – М.: Изд-во «Горячая линия – Телеком», 2014 г.
2.
Васин В.А., Калмыков В.В., Себекин Ю.Н., Сенин А.И., Федоров И.Б. Радиосистемы передачи
информации. Учебное пособие для вузов / Под ред. И.Б. Федорова и В.В. Калмыкова. – М.: Издво «Горячая линия – Телеком», 2015 г.

4.

Дополнительная литература
1.
Теория электрической связи: учебное пособие / К.К. Васильев, В.А. Глушков, А.В. Дормидонтов, А.Г. Нестеренко; под общ. ред.
К.К. Васильева. – Ульяновск: УлГТУ, 2008. – 452 с.
2.
Бернард Скляр. Цифровая связь. Теоретические основы и практическое применение: Пер. с англ. – М.: Издательский дом
«Вильямс», 2003. – 1104 с.
3.
Каганов В.И., Битюков В.К. Основы радиоэлектроники и связи: Учеб. пособие для вузов. – М.: Горячая линия-Телеком, 2007. –
542 с.
4.
Стеценко О.А. Радиотехнические цепи и сигналы: Учебник. – М.: Высш. шк., 2007. – 432 с.
5.
Периодические издания: журнал «Вестник»; «Вестник связи»; «Автоматика, Связь, Информатика».
6.
Основы теории электрической связи. Учеб. Пособие/ под ред. А.Н. Путилина.- СПб.: ВАС, 1997.- 155 с.
7.
Прокис Дж. Цифровая связь.- М.: Радио и связь, 2000,- 797 с.
8.
Электросвязь. Введение в специальность: Учеб. пособие для вузов/ В.Г. Дурнев, А.Ф. Зелевич, Б.И. Крук и др.- М.: Радио и
связь, 1988.-240 с.

5.

6.

Периодическими называют сигналы, обладающие следующим свойством:
Такие функции, удовлетворяющие условиям Дирихле, можно описать суммой
тригонометрического ряда (ряда Фурье):
(1)
где

7.

Формула (1) ряда Фурье удобна с точки зрения простоты вычисления
коэффициентов разложения ak и bk. Ряд Фурье можно записать иначе:
где

8.

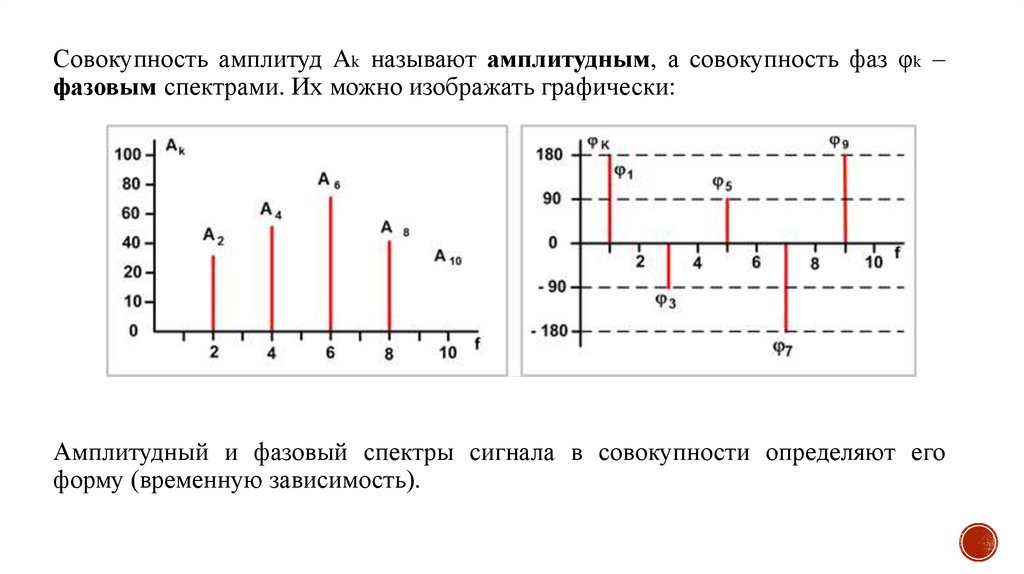
Совокупность амплитуд Ak называют амплитудным, а совокупность фаз φk –
фазовым спектрами. Их можно изображать графически:
Амплитудный и фазовый спектры сигнала в совокупности определяют его
форму (временную зависимость).

9.

10.

Т – финитными называют ограниченные по времени сигналы. По определению
они не могут быть периодическими и, следовательно, к ним не применимо
разложение в ряд Фурье.
Для описания таких сигналов применим приём:
На первом этапе от заданного сигнала х(t), имеющего начало в точке t1 и конец
в точке t2 , переходим к сигналу xn(t), который является периодическим
повторением х(t) на бесконечной оси времени с периодом
Данный сигнал можно разложить в ряд Фурье:
где

11.

Для
описания спектра финитного сигнала приходим к известному в
математике интегральному преобразованию Фурье:
– прямое преобразование
– обратное преобразование
Из полученных соотношений следует, что спектр Т-финитного сигнала
сплошной. Он представляет собой совокупность бесконечного числа
составляющих с бесконечно малыми амплитудами, непрерывно следующих по
оси частот.
– амплитудный спектр
– фазовый спектр

12.

13.

1.
Прямое и обратное преобразования Фурье являются линейными
операторами, следовательно, действует принцип суперпозиции.
Если
то
,
2.
Прямое и обратное преобразования Фурье являются взаимно однозначными.
3.
Свойство запаздывания.
Если
,
то

14.

Спектральная функция δ – функции равна 1. Спектральная функция
комплексного гармонического сигнала равна:
Скалярное произведение комплексных сигналов в спектральной области:
Из полученного результата для вещественных функций x(t) вытекает равенство
Парсеваля (обобщённая формула Релея):
– энергия сигнала x(t).

15.

Теоретически ширина спектра сигнала бесконечна. Однако, учитывая, что
интенсивность спектральных составляющих реальных сигналов уменьшается с
ростом их частоты, то можно ввести понятие практической (конечной) ширины
спектров.
Практическую ширину спектра можно определить как ширину частотного
интервала, в пределах которого амплитудный спектр S(ω) не меньше некоторого
уровня γ, например, γ = 0,1 от S(ω)max.
Принципиально важно: произведение ширины спектра на длительность сигнала
есть константа, зависящая только от формы импульса. Следовательно, чем
короче сигнал, тем шире его спектр, и, тем более широкополосный канал
требуется для его передачи.
Методы Фурье используются для анализа линейных схем или систем:
‒ для предсказания реакции (отклика) системы;
‒ для определения динамики системы (передаточной функции);
‒ для оценки или интерпретации результатов тестов.