Похожие презентации:
Юмор вокруг математики
1.
Сидят три ряда. Вдруг одинначинает сходиться. Другие ему:
«Схождение без причины –
признак Даламбера».
1
lim
x 8 8 x
1
lim
x 3 3 x
3
- Понятно?
- Да!
- Решите похожий
пример
- Решили
Убит тяжёлым,
тупым предметом…
1
2 3
3 2
Пол пиццы
на троих –
каждому по
полторы??!
2.
Положительныечисловые ряды
3.
an 1
Знакопостоянные
ряды
n (an 0) (an 0)
Положительные
ряды
n an 0
Отрицательные
ряды
n an 0
n
Знакопеременные
ряды
Знакочередующиеся
ряды
n 1
(
1
)
an , an 0
n 1
4.
Общий признак сходимостиположительных рядов (необходимое и
достаточное условие сходимости ряда)
Для того чтобы положительный ряд
сходился, необходимо и достаточно, чтобы
последовательность его частичных сумм
была ограничена сверху.
a , an 0
n 1
n
lim S n S
n
n S n 1 S n an 1 S n
{S n } неубывающая
sup S n
n N
5.
Первый признак сравненияПусть даны два положительных ряда
a b
n
n 1
n 1
n
N : n N 0 an bn
b сходится
n 1
an сходится
n
n 1
bn расходится
an расходится
n 1
n 1
n 1
n 1
миноранта bn мажоранта
a
n
6.
Предельный признак сравненияПусть даны два положительных ряда
a b
n
n 1
n 1
n
an
lim K R \ {0}
n b
n
a сходится
n 1
n
an расходится
n 1
b сходится
n
n 1
b расходится
n 1
n
7.
ЗамечаниеПри сравнении рядов один из рядов называется
эталонным, т.е. ряд с которым сравнивают и при
который заранее известно сходится он или расходится .
В качестве эталонных выбирают или геометрические
ряды, или обобщенные гармонические ряды (частные
случаи рядов Дирихле).
1
1 1 1 1
1 ...
2 3 4 5
n 1 n
Гармонический ряд расходится
8.
Геометрический рядРяд составленный из членов бесконечной
геометрической прогрессии (геометрический
ряд)
n
c q ( с 0)
n 0
сходится при |q|<1 и расходится при |q|≥1.
c q с cq cq ... cq
n
2
n 0
S n с cq cq ... cq
2
n 1
n 1
...
c(1 q )
1 q
n
9.
Интегральный признак Коши – Маклоренаa , a 0
n 1
n
x [1; ) f ( x) :
Производящая
n an f (n)
функция
n
f(x) – непрерывная положительная (f(x)>0) и
невозрастающая (x1< x2 → f(x1) ≥ f(x2)).
сходится
f
(
x
)
dx
1
f ( x)dx K R
1
a сходится
n 1
n
an расходится
f ( x)dx расходится
n 1
1
f ( x)dx
1
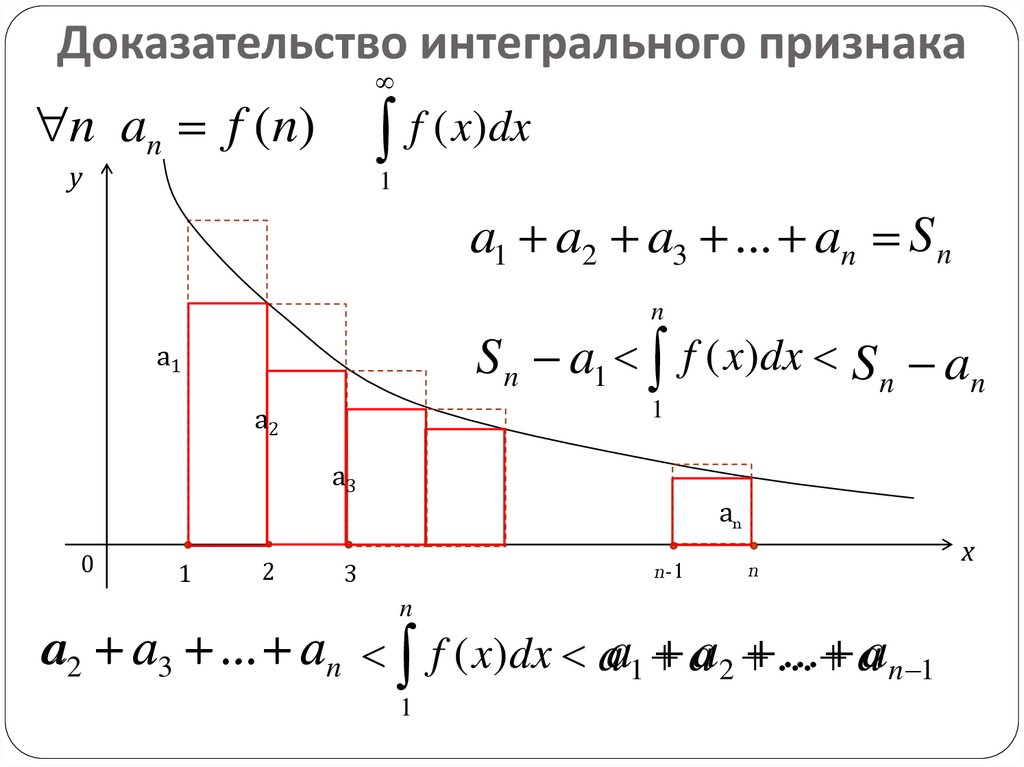
10.
Доказательство интегрального признакаf ( x)dx
n an f (n)
у
1
a1 a2 a3 ... an S n
n
S n a1 f ( x)dx S n an
а1
1
а2
а3
0
1
2
аn
n-1
3
n
n
a2 a3 ... an f ( x)dx aa1 a 2 ...
... aan 1
1
х
11.
Доказательство интегрального признакаn an f (n)
f ( x)dx
n
a , a 0
n 1
1
S n a1 f ( x)dx S n an
n
n
{S n } возрастающая
1
1) сходится
f ( x)dx A, A R
1
S n a1 A
lim S n S
n
n
1
1
f ( x)dx f ( x)dx A
S n A a1
{S n } огранич. сверху
a сходится
n 1
n
n
f ( x)dx M 0 f ( x)dx M
1
M 0 S n M an lim S n a расходится
n
2) расходится
1
n 1
n
12.
Обобщенный гармонический рядс
сходится при 1,
(c 0)
n 1 n
расходится при 1
Интегральный признак Коши – Маклорена
1
f ( x) x [1; ) – непрерывная,
x
0
убывающая
для
f(x)>0
dx
1 f ( x)dx 1 x 1 ln | x | 1
1
x
1
1 1
1
1
1
1
(1 ) x 1 1
13.
Признак Коши(радикальный)
n a q
lim
an , an 0 n n
n 1
q 1 an сходится
n 1
q 1 an расходится
n 1
Огюсте́ н Луи́ Коши́
(1789 — 1857) —
фр. математик и
механик
N : n N
n
a n 1 an расходится
n 1
14.
Признак Даламбераa n 1
lim
q
a
,
a
0
n
n
n a
n
n 1
q 1 an сходится
Jean Le Rond D'Alembert
(1717 — 1783) фр.
математик, механик,
энциклопедист
N : n N
n 1
q 1 an расходится
n 1
an 1
1 an расходится
n 1
an
15.
Доказательство признака Даламбераa n 1
lim
q
n a
n
an 1
q
an
0 N ( ) : n N
an 1
q
an
an 1
q
q
an
(q ) an an 1 (q ) an
1) q 1
: (q ) 1
an 1 (q ) an
(q ) b
an 1 b an
n N
16.
Доказательство признака Даламбераa n 1
lim
q
n a
n
Пусть
N 1
a2 b a1
1) q 1 : (q ) 1 (q ) b
n N
a3 b a2 b a1
a4 b a3 b a1
3
……………………………..
an b an 1 b n 1 a1
……………………………..
n
a b a1 a1 b n
n 2
0 b 1
2) q 1
an 1
lim
q 1
n a
n
2
an 1 b an
n
n 1
n 1
Сходится по первому пр. сравнения
N : n N
an 1
an 1 an
1
an
lim an 0
n
Расходится по достат. пр. расходимости
17.
Признак Раабеa , a 0
n
n
an
lim n
1 q
n
a
n 1
q 1 an сходится
n 1
Йозеф Людвиг Раабе
(1801 – 1859)
швейцарский
математик
N : n N
n 1
q 1 an расходится
n 1
an
n
1 1 an расходится
n 1
a n 1
18.
an 1
n
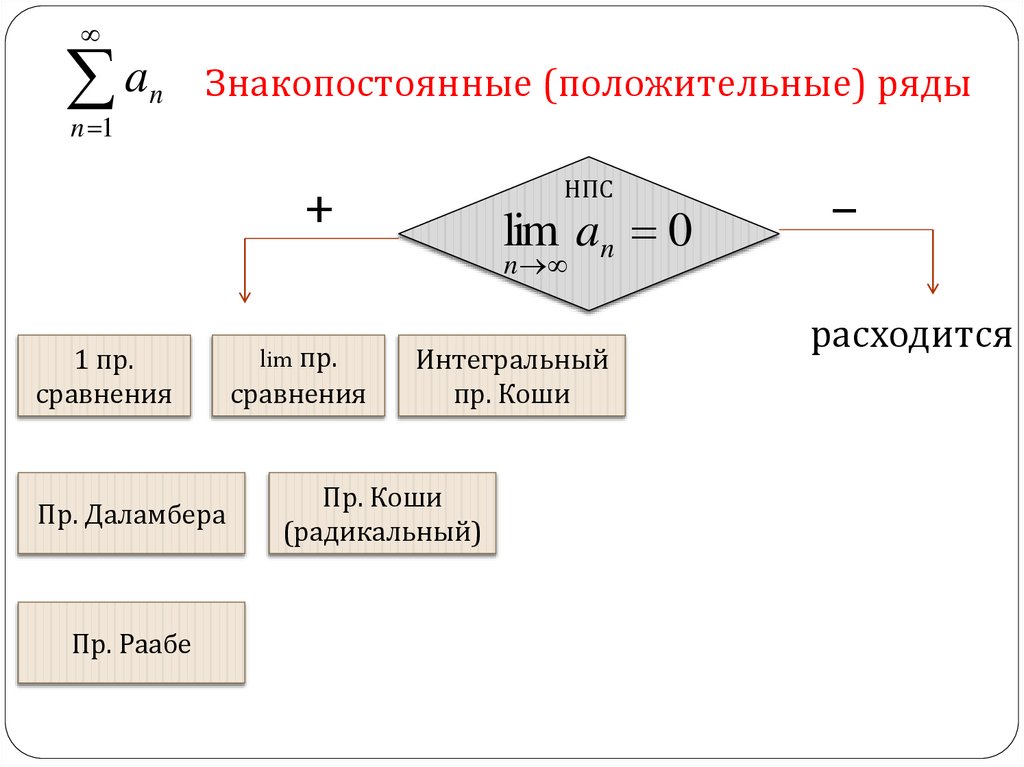
Знакопостоянные (положительные) ряды
+
НПС
lim an 0
–
n
1 пр.
сравнения
Пр. Даламбера
Пр. Раабе
lim пр.
сравнения
Интегральный
пр. Коши
Пр. Коши
(радикальный)
расходится
















 Математика
Математика Юмор
Юмор








