Похожие презентации:
Дифференцирование явно заданных функций
1.
Дифференцированиеявно заданных
функций
1
2.
Производные идифференциалы
первого порядка
2
3.
Найти частные производные первого порядка функции:К 3.1.3. f x, y sin x x 2 y .
К 3.3.1. f x, y, z xy yz zx .
К 3.13.1. Найти дифференциал функции f x, y 2 x 4 3x 2 y 2 x3 y .
К 3.14.2. Найти точки, в которых дифференциал функции f равен 0, если
f x, y, z 2 y 2 z 2 xy 2 yz 4 x 1 .
К 3.18.1. Найти дифференциал функции f в точке 1,0,1 , если f x, y, z
К 3.40.1. Найти градиент функции f x, y 1 x 2 y 3 в точке 1,1 .
x
x2 y2 z2
К 3.39.1. Найти производную функции f x, y 3x 2 5 y 2 по направлению вектора
1 1
l =
,
в точке M 1,1 .
2 2
К 3.43.1. Найти производную функции f x, y 5 x 10 x 2 y y 2 в точке M 0
по направлению вектора M 0 M , если M 0 1,2 , M 5, 1 .
f
К 3.48.1. Найти наибольшее значение
в т. M 1,1 , если f xy 2 3x4 y5 .
l
f
К 3.49.1. Найти единичный вектор l , по направлению которого
в т. M достигает
l
наибольшего значения, если f x , y x 2 xy y 2 , M 1,2 .
3
4.
Найти частные производные первого порядка функции:К 3.1.3. f x, y sin x x 2 y .
К 3.3.1. f x, y, z xy yz zx .
4
5.
Найти частные производные первого порядка функции:К 3.1.3. f x, y sin x x 2 y .
К 3.3.1. f x, y, z xy yz zx .
f x cos x 2 xy ,
f x y z ,
f y x 2
f y x z ,
f z y x
5
6.
К 3.13.1. Найти дифференциал функцииf x, y 2 x 3x y x y .
4
2
2
3
6
7.
К 3.13.1. Найти дифференциал функцииf x, y 2 x 3 x y x y .
4
2
2
3
Способ 1.
3
2
2
2
3
df 8 x 6 xy 3x y dx 6 x y x dy
Способ 2.
df 8 x dx 6 xy dx 6 x ydy 3x ydx x dy
3
2
2
2
3
7
8.
К 3.14.2. Найти точки, в которых дифференциалфункции f равен 0, если
f x, y, z 2 y 2 z 2 xy 2 yz 4 x 1 .
8
9.
К 3.14.2. Найти точки, в которых дифференциалфункции f равен 0, если
f x, y, z 2 y 2 z 2 xy 2 yz 4 x 1 .
2
y
4
2
f x y 4 0
4y z 7
f y 4 y 2 xy z 0 x
2y
4
f 2z y 0
z
y
z
2
7
7
Ответ: , 2,1 и , 2, 1 .
4
4
9
10.
К 3.18.1. Найти дифференциал функции f в точке 1,0,1 , еслиx
f x, y , z 2 2 2
x y z
10
11.
К 3.18.1. Найти дифференциал функции f в точке 1,0,1 , еслиx
f x, y , z 2 2 2
x y z
x y z x 2x
f x
0
2
2
2 2
x y z 1,0,1
x 2 y
1
fy
0 df 1,0,1 dz .
2
2
x 2 y 2 z 2 1,0,1
x 2z
1
f z
2
2
2 2
2
x
y
z
1,0,1
2
2
2
11
12.
К 3.40.1. Найти градиент функции f x, y 1 x 2 y 3в точке 1,1 .
12
13.
К 3.40.1. Найти градиент функции f x, y 1 x 2 y 3в точке 1,1 .
grad f 1,1 2 xy 3 ,3x 2 y 2
1,1
2,3
Второй способ записи:
grad f 2 xy 3 ,3 x 2 y 2
1,1
2,3 .
13
14.
К 3.39.1. Найти производную функцииf x, y 3 x 2 5 y 2
1 1
по направлению вектора l =
,
в точке M 1,1 .
2 2
14
15.
К 3.39.1. Найти производную функцииf x, y 3x 2 5 y 2
1 1
по направлению вектора l =
,
в точке M 1,1 .
2 2
f
1 1
grad f , l0 6 x,10 y
,
2 2 .
l
2 2 1,1
15
16.
К 3.43.1. Найти производную функцииf x, y 5 x 10 x 2 y y 2
в точке M 0 по направлению вектора M 0 M , если
M 0 1,2 , M 5, 1 .
16
17.
К 3.43.1. Найти производную функцииf x, y 5 x 10 x 2 y y 2
в точке M 0 по направлению вектора M 0 M , если
M 0 1,2 , M 5, 1 .
a = M 0 M 4, 3 ,
f
4 3
2
grad f , a0 5 20 xy, 10 x 2 y ,
a
5 5 1,2
4 45 3 14 138
.
5
5
17
18.
fК 3.48.1. Найти наибольшее значение
в т. M 1,1 ,
l
если f xy 2 3x 4 y 5 .
18
19.
fК 3.48.1. Найти наибольшее значение
в т. M 1,1 ,
l
если f xy 2 3x 4 y 5 .
2
3 5
4 4
l
=
gradf
y
12
x
y
,
2
xy
15
x
y
1,1
f
grad f
grad f , l0 grad f ,
l
grad f
1,1
11, 13 ,
grad f 290 .
19
20.
К 3.49.1.Найти единичный вектор l , по направлениюf
которого
в т. M достигает наибольшего значения, если
l
f x, y x 2 xy y 2 , M 1,2 .
20
21.
К 3.49.1. Найти единичный вектор l , по направлениюf
которого
в т. M достигает наибольшего значения, если
l
f x, y x 2 xy y 2 , M 1,2 .
grad f
l
,
grad f
gradf 2 x y, x 2 y 1,2 4,5
5
4
l
,
.
41 41
21
22.
Производные идифференциалы
старших порядков
22
23.
К 4.6.1. Найти частные производные второго порядкаf x 1 y z .
2 3
23
24.
К 4.6.1. Найти частные производные второго порядкаf x 1 y 2 z 3 .
2 3
f x 1 y z
f y 2 xyz 3
f z 3xy 2 z 2
f xx 0
3
f yy 2 xz
f zz 6 xy 2 z
3
f xy f yx 2 yz
2
f yz f zy 6 xyz
f zx f xz 3 y 2 z 2
24
25.
К 4.14. Найти второй дифференциал функции f x, y , если1) f x, y x 1 y ,
2) f x , y x sin 2 y .
25
26.
К 4.14. Найти второй дифференциал1) f x, y x 1 y .
Способ 1.
df dx 1 y xd 1 y dx 1 y xdy
d 2 f d dx 1 y xdy
2
2
d
x 1 y dx d 1 y dxdy x d
y 2dxdy
0
0
dy
Способ 2. Используя символическую формулу
f x 1 y f xx f yy 0
2
d
f 2 1 dxdy
f x
f 1
y
xy
C21,1
f xy
26
27.
К 4.14. Найти второй дифференциал2) f x, y x sin 2 y .
f x sin 2 y
f y x 2sin y cos y x sin 2 y
f xx 0
f yy 2 x cos 2 y
f xy sin 2 y
2
d 2 f 2 sin
2
y
dxdy
1
2
x
cos
2
y
dy
1,1
0,2
C2
f xy
C2
f xy
2sin 2 y dxdy 2 x cos 2 y dy 2
27
28.
К 4.17.1. Найти второй дифференциал функцииf x, y, z xy yz zx
28
29.
К 4.17.1. Найти второй дифференциал функцииf x, y, z xy yz zx
f x y z
f y x z
f xy f yz f zx 1,
f z y x
C21,1,0 C20,1,1 C21,0,1 2
d 2 f 2 dxdy dydz dxdz .
29
30.
К 4.18.1. Найти в точке M 0,0,0 второйдифференциал функции
f x, y, z x 2 y 3z 2 xy 4 zx 2 yz .
4
3
2
30
31.
К 4.18.1. Найти в точке M 0,0,0 второйдифференциал функции
f x , y , z x 2 y 3z 2 xy 4 zx 2 yz .
4
f x 4 x 2 y 4 z
2
f y 6 y 2x 2z
f z 6 z 4 x 2 y
3
2
d f
3
2
f xx 12 x 2
M
0
f yy 12 y M 0
f zz 6
f xy 2
f yz 2
f zx 4
6 dz 2 2dxdy 2dydz 4dxdz
2
M
31
32.
К 4.21.1. Найти d f , если f x, y x y .3
2
32
33.
К 4.21.1. Найти d f , если f x, y x y .3
2
f x 2 y dx dy 6dx dy
d f С
3
3
2,1
3
2
2
2
33
34.
К 4.22.4. Найти d 3 f в точке M 0,1, 2 , еслиf x , y , z x 4 xy 2 yz 2 zx 2 .
34
35.
К 4.22.4. Найти d f в точке M 0,1,2 , если3
f x, y, z x xy yz zx .
4
2
2
2
4 3 2 x 24 x M 0,
f xxx
f xy 2 f yz 2 f zx 2 2
1,2,0
3
C
3
d f
C
0,1,2
3
C
2,0,1
3
6 dxdy dydz dzdx
2
M
3
2
2
35
36.
П р и м е р 1.13. Найти d 14 f , если f x, y , z z16 y15 2 x 7 y 3 z 4 7 x 3 z 2 y 4 5 x 9 y 7 .Выпишем сначала все ненулевые частые производные 14-го порядка:
14 f 16! 2
– от первого слагаемого 14
z ;
z
2
14 f
– от второго слагаемого 14 15! y ;
y
14 f
– от третьего слагаемого 7 3 4 2 7!3!4!;
x y z
– от четвертого слагаемого все частные производные 14-го порядка нулевые;
– от пятого слагаемого
14
14
14 f
9!
f
f
7! 2
2
,
,
5
7!
x
5
9!7!
xy
5
9!
y .
7
7
8
6
9
5
x y
2!
x y
x y
2!
Используя символическую формулу получим:
14 f 14 14 f 14
14 f
14
7,3,4
7
3
4
d f 14 dz 14 dy C14
dx
dy
dz
7
3
4
z
y
x y z
C
7,7
14
14
14
14 f
7
7
8,6 f
8
6
9,5 f
9
5
dx
dy
C
dx
dy
C
dx
dy
,
14
14
7
7
8
6
9
5
x y
x y
x y
где частные производные функции f x, y , z уже вычислены.
36
































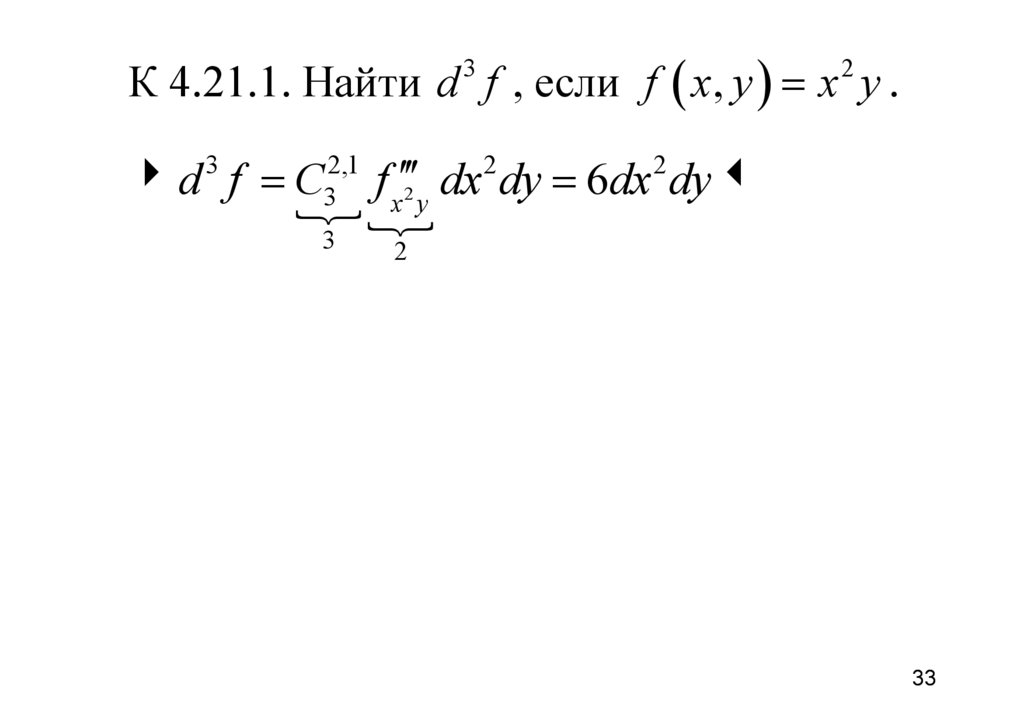



 Математика
Математика








