Производная сложной и обратной функций. Дифференцирование неявной и параметрически заданной функции

1.

Первое высшее техническое учебное заведение России
Санкт-Петербургский горный университет императрицы
Екатерины II
Раздел: Дифференциальное исчисление функции
одной переменной
Лекция 2. Производная сложной и обратной
функций. Дифференцирование неявной и
параметрически заданной функции
18.03.2025
г. СанктПетербург
2025
1/15

2.

Содержание лекции
1. Правила дифференцирования сложной и
обратной функций
2. Рассмотреть параметрическое и неявное задания
функций и их дифференцирование.
3. Логарифмическое дифференцирование функций
2|15

3.

Производная сложной функции
Функция y = F (u ) , где u = j (x) , т.е. y = F (j ( x)) называется сложной
функцией переменной х, где u - промежуточный аргумент.
Теорема. Пусть функция u = j (x) имеет в точке х производную u ¢x = j ¢(x) ,
а функция y = F (u ) в соответствующей точке u имеет производную yu¢ = F ¢(u ) .
Тогда производная сложной функции y = F (j ( x)) : y ¢x = y u¢ × u ¢x
Доказательство:
Дадим x приращение Dx
переменная u получит приращение
переменная y получит приращение
По определению производной:
Du = j ( x + Dx ) - j ( x )
Dy = F (u + Du ) - F (u )
Dy Du
Dy
D
y
D
u
×
= lim
y ¢ = lim
= lim
× lim
Dx ®0 Du Dx
Dx ®0 Dx
Dx ®0 Du Dx ®0 Dx
функция u = j (x) - непрерывна Du ® 0 при Dx ® 0
Dy
lim
Du ®0 Du
yu¢
3|15
u ¢x

4.

Замечание: правило остается в силе, если промежуточных аргументов несколько:
y=F(u), u=u(t), t=t(x) y¢x = yu¢ × ut¢ × t ¢x
Пример 1. Найти производную
функции y=ln(x2+ x+ 5)
производная аргумента
y' =
1
2
x + x+5
2
( x + x + 5)' =
производная внешней функции
y=ln u, u= x2+ x+ 5
Пусть функция у=f(x) - определена, строго монотонна
и непрерывна на множестве Х, а У - множество ее значений.
Тогда на множестве У существует обратная функция x= (y) ,
которая непрерывна и строго монотонна.
Взаимно обратные функции:
y = 2x
х =log2 y
х (– ,+ ) у (0,+ )
4|15
2x +1
x2 + x + 5

5.

Теорема (производная обратной функции)
Если функция y = f (x) в точке х0 имеет производную f ¢( x0 ) ¹ 0, то обратная функция
1
¢
x = j ( y ) в соответствующей точке y0 = f ( х0 ) имеет производную j ( y 0 ) = f ¢( x )
0
Доказательство:
.
Аргументу у обратной функции x = j ( y ) в точке y0 зададим приращение Dу ¹ 0
Функция строго монотонна
ее приращение Dх ¹ 0
Перейдем в равенстве к пределу при Dy ® 0
Из непрерывности функции
Функция у=arcsin х
j ¢( y 0 )
Dx
1
=
Dy Dy
Dx
Dx ® 0
f ¢( x0 )
возрастает на отрезке [ 1;1]
и является обратной для функции x=sin y , которая возрастает на отрезке [ π/2; π/2]:
(arcsin x )¢ x =
1
1
1
=
=
=
(sin y )¢ y cos y 1 - sin 2 y
5|15
1
1- x
2

6.

каждому значению t
x
=
j
(
t
);
ì
Дифференцирование функции, f (x) :
t Î [a ; b ] соответствует только
í
одно значение
заданной параметрически
î y = y (t ),
координат х и у
Пример 2. Установить вид кривой из
параметрических уравнений
Исключим параметр t :
x = r cos t ; y = r sin t
t Î [0; p ]
-r
y = r 2 - x2
Пусть функция у=f(x) определена и непрерывна на отрезке [a, b]
Кривую можно задать параметрически: x = t ; y = f (t ), t Î [a; b]
Теорема. Если функция y (x) задана параметрическими уравнениями:
x=x(t), y=y(t), t Î [a ; b ] , где x(t)- непрерывна и строго монотонна,
x(t) и y(t) – дифференцируемые функции по t и xt¢ ¹ 0 , то ее производная равна:
yt¢
y¢x =
, ( xt¢ ¹ 0)
xt¢
6|15
r

7.

Доказательство:
Функция x=x(t) - непрерывна
и строго монотонна
y=y(х) – сложная функция,
где x=x(t), t=Ф(х)
Существует обратная функция
t = F (x) –
непрерывная, строго монотонная и дифференцируемая
y ¢x = yt¢ × t ¢x
1
xt¢
yt¢
y ¢x =
, ( xt¢ ¹ 0)
xt¢
ì x = cos t ,
t Î [0; p ]
í
Пример 3. Найти производную функции, заданной параметрически î y = sin t ,
Функция cos t при t [0; ] строго убывает
и существует обратная функция t=arccos x
xt¢ = - sin t
yt¢ = cos t
y = sin(arccos x) = 1 - cos 2 (arccos x) = 1 - x 2
cos t
¢x =
y
= -ctgt
- sin t
7|15
Системой задается верхняя
полуокружность

8.

Дифференцирование неявной функции
Пусть значения двух переменных х и у связаны между собой уравнением
F ( x, y ) = 0
Если на некотором интервале (a,b) каждому значению переменной x соответствует
единственное значение переменной y (которое вместе с x обращает уравнение в
тождество), то говорят, что уравнение задает неявную функцию y=f(x).
Если функция y(x) дифференцируема в интервале (a,b), то дифференцируя тождество можно
найти производную неявной функции.
Пример 4. Найти производную y¢x из уравнения x 3 + y 3 - 3xy = 0 .
y - функция от x
Продифференцируем по x обе части уравнения
(x ) + (y )
3 ¢
3x
2
3 ¢
¢
- (3 xy ) = 0
3 y y ¢ 3( y + xy ¢)
2
8|15
2
2
x
+
y
y ¢ - ( y + xy ¢) = 0
y ¢( y 2 - x) = y - x 2 ;
y ' = ( y - x 2 ) /( y 2 - x)

9.

3
¢
y
2
y
=
1
+
xy
Пример 5 Найти производную x в точке M (1;1), если
.
Продифференцируем обе части уравнения по х:
Полагая x = 1 и y = 1
3
2
¢
2 y х = y + 3 xy y ¢х
2 y ¢х = 1 + 3 y ¢х y ¢х М = -1
Замечание. Уравнение F ( x, y ) = 0 определяет также неявную функцию х( у ) .
Чтобы найти производную x¢y , нужно продифференцировать обе части этого уравнения по y
и из полученного равенства определить x¢y
-t
¢
t
s
=
t
e
Пример 6. Найти производную s , если задана обратная функция
Производная обратной функции:
t
1
1
e
-t
-t
-t
=
=
e
(1 - t ) t s¢ =
st¢ = e - t e =
t
st¢ e (1 - t ) 1 - t
9|15

10.

Логарифмическое дифференцирование
v( x)
y
=
u
(
x
)
Степенно-показательная функция:
ln y ( x) = v( x) ln(u ( x))
Продифференцируем левую и правую часть этого равенства по х:
1
1
× y ¢x (x )= v¢( x) × ln u ( x) + v( x) ×
× u ¢( x)
y
u ( x)
y ¢x (x ) = [u ( x)]
v( x)
1
(v¢( x) × ln u ( x) + v( x) ×
× u ¢( x)).
u ( x)
Пример 7. Найти производную функции y = x sin x
ln y = ln x
sin x
ln y = sin x ln x
1
sin x
y ' = cos x ln x +
y
x
10|15
y' = x
sin x æ
sin x ö
ç cos x ln x +
÷
x ø
è

11.

Прием логарифмического дифференцирования удобен,
если требуется продифференцировать:
– степенно-показательную функцию,
– произведение нескольких функций,
– дробь, числитель и знаменатель которой содержат произведения.
11|15

12.

2
x
=
3
t
5
и
y
=
t
- 4 найти
Пример 8. Для параметрически заданной кривой:
уравнения касательной и нормали в точке M 0 ( 4; 5) .
Найдем значение параметра t, соответствующее точке
ì4 = 3t - 5;
í
2
5
=
t
-4
î
Þ t=3
Угловой коэффициент касательной:
Уравнение
касательной:
M 0 (4, 5)
æ yt¢ ö
2t
ç
÷
=2
k = y ¢x M 0 = ç ÷ t =3 =
3
è xt¢ ø
Уравнение
нормали:
y - y0 = f ¢( x0 )( x - x0 ).
y - 5 = 2( x - 4)
y = 2x - 3
1
y - y0 = ( x - x 0 ).
f ¢( x 0 )
1
y - 5 = - ( x - 4)
2
1
y =- x+7
2
12|15

13.

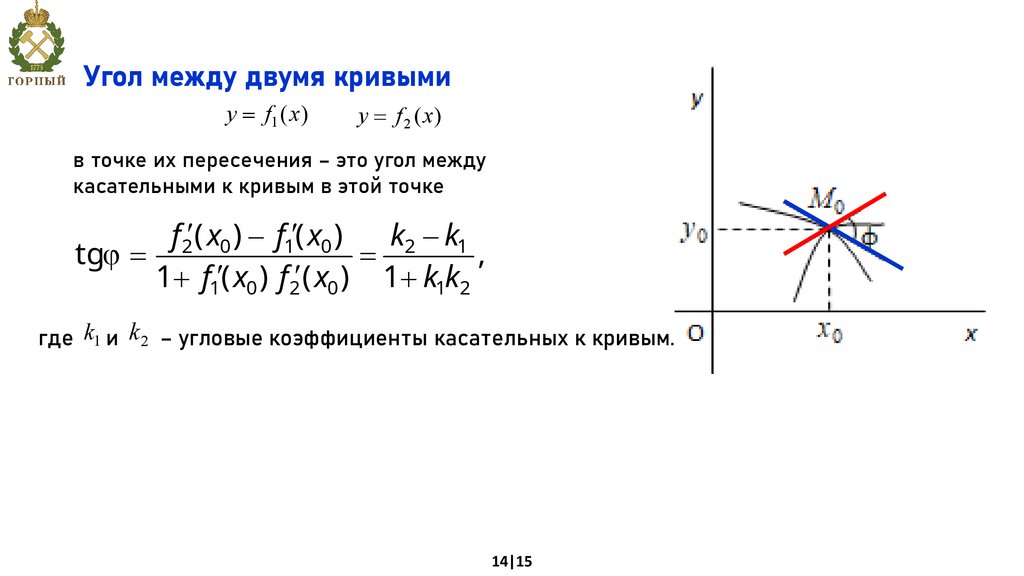
Угол между двумя кривыми
y = f1 ( x )
y = f 2 ( x)
в точке их пересечения – это угол между
касательными к кривым в этой точке
f2¢( x0 ) - f1¢( x0 )
k2 - k1
tgj =
=
,
1+ f1¢( x0 ) f2¢( x0 ) 1+ k1k2
где k1 и k 2 – угловые коэффициенты касательных к кривым.
14|15

14.

Спасибо за внимание
Санкт-Петербургский горный
университет
императрицы Екатерины II,
г. Санкт-Петербург,
Малый пр. В.О., д. 83
Тел.: +7(812) 328-82-98;
15|15