Функциональные ряды

1.

7. Функциональные ряды

2.

Функциональная последовательность
Занумерованное множество функций {fn(x)} с одной и той
же областью определения D называется функциональной
последовательностью, а множество D – областью
определения последовательности.
2
3
n
1, x, x , x , ..., x , ...
D: R
1 1 1
1
1, , 2 , 3 , ..., n , ...
x x
x
x
D : R \ {0}
1
1
1
1
( 1) n 1
,
,
,
, ...,
, ... D : R \ N
x 1 x 2 x 3 x 4
x n

3.

Функциональный ряд
Ряд называется функциональным, если его члены являются
функциями от х, которые определены на некотором множестве X
f ( x) f ( x) f ( x) f ( x) ... f ( x) ...
n 1
n
1
2
3
n
1
1 1
1
1
1 2 3 ... n ...
n
x x
x
x
n 0 x
1
1
x 1 n 1 расходится x
2
n 0 1
n 0
n
1
1 сходится
x 2 2n 2
n 0
n 0
D : R \ {0}
2
n
n 0
расходится
| x | 1
Область сходимости

4.

Область сходимости ряда
f ( x)
n 1
n
Значение х=х0, при котором числовой ряд сходится,
называют точками сходимости.
Область сходимости X функционального ряда –
совокупность всех точек сходимости функционального
ряда или множество таких значений переменной х∈X, при
которых функции fi(x) определены и при подстановке
каждого из которых в fn (x) полученный числовой ряд
будет сходящимся.
Область расходимости – совокупность значений,
делающих его расходящимися.

5.

Область сходимости ряда f n ( x)
n 1
Область сходимости функционального ряда находится с
помощью непосредственного применения признака
Даламбера или радикального признака Коши для ряда,
составленного из абсолютных величин членов данного
функционального ряда
f n ( x)
n 1
f n 1 ( x)
lim
n f ( x )
n
lim n f n ( x)
n

6.

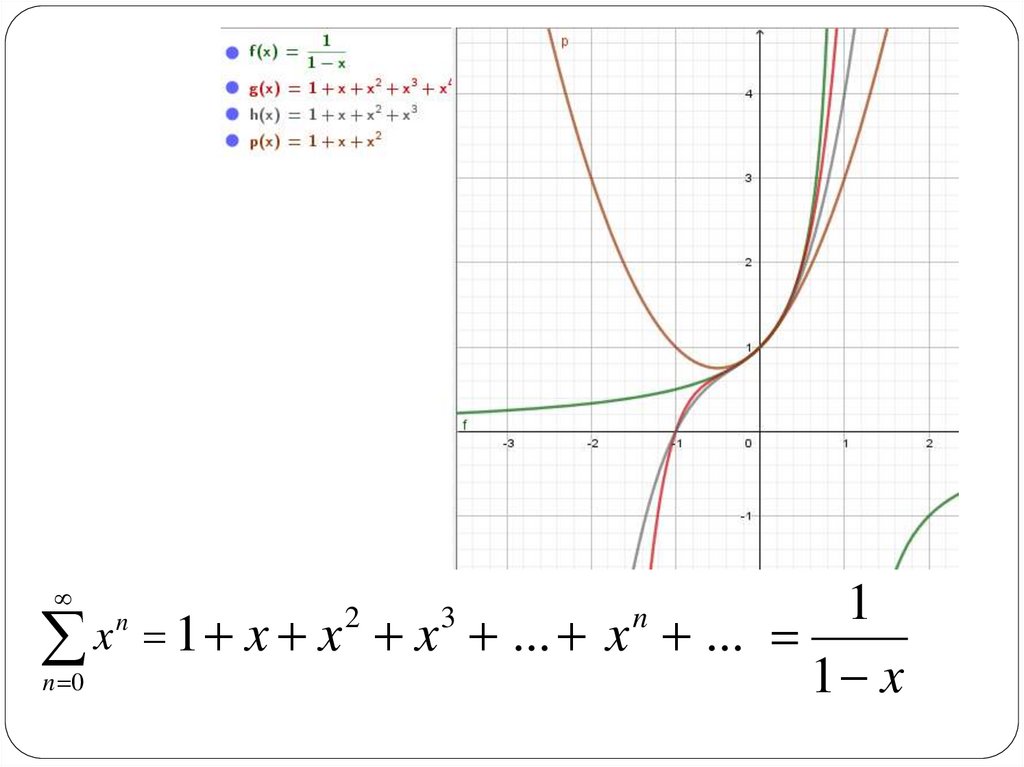
1
x 1 x x x ... x ...
n 0
1 x
n
2
3
n

7.

Функциональный ряд
Ряд называется функциональным, если его члены являются
функциями от х, которые определены на некотором множестве X
f ( x) f ( x) f ( x) f ( x) ... f ( x) ...
n 1
n
1
2
3
n
S n ( x) f1 ( x) f 2 ( x) ... f n ( x)
п-ая частичная сумма функционального ряда (функция
переменной х)
lim S n ( x) S ( x) сумма функционального ряда
n
Rn ( x) S ( x) S n ( x)
п-й остаток ряда
В точках, не принадлежащих области сходимости, частичная сумма не
имеет предела.

8.

Сходимость и равномерная f ( x)
n
n 1
сходимость
lim S n ( x) S ( x)
n
S n ( x) S ( x)
0 N N ( , x0 ) : n N
lim Rn ( x) 0
n
S n ( x) S ( x)
Функциональный ряд сходится равномерно на множестве Х
S n ( x) S ( x)
0 N N ( ) : n N
S n ( x) S ( x)

9.

Достаточный признак равномерной
сходимости функционального ряда
(Признак Вейерштрасса)
Если для членов функционального ряда f n ( x)
n 1
начиная с некоторого номера N и всех х∈Х (области
сходимости) выполняются неравенства |fn(x)|<an, где an –
некоторое число не зависящее от х и при этом an
n 1
сходящийся положительный числовой ряд, то этот f n ( x)
функциональный ряд сходится равномерно на Х.
n 1
Функциональный ряд называется мажорируемым в
некоторой области Х, а числовой ряд в этом случае
называют мажорирующим (усиливающим) или
мажорантой по отношению к функциональному ряду.

10.

Свойства равномерно
сходящихся рядов
1) Если ряд f n ( x ) на множестве Х сходится
n 1
равномерно к сумме S(x), а функции fn(x) определены и
непрерывны на этом множестве, то и сумма S(x) будет
непрерывной функцией на Х.
f ( x) на отрезке [a; b] сходится
2) Если ряд
n 1
n
равномерно к сумме S(x), функции fn(x) определены и
непрерывны на этом же множестве, то его можно
почленно интегрировать на отрезке [a; b] :
b
b
b
f ( x)dx S ( x)dx f ( x)dx
a n 1
n
a
n 1 a
n
Интеграл от суммы ряда равен сумме ряда, составленного
из интегралов от членов данного ряда.
Если x1 и x2 xx
любые две точки отрезка [a; b] , то
f ( x)dx
f ( x)dx
2
x1 n 1
2
n
n 1 x1
n

11.

Свойства равномерно
сходящихся рядов
f n ( x ) на отрезке [a; b] сходится к сумме
3) Если ряд
n 1
S(x), функции fn(x) определены и непрерывны на [a; b] и
непрерывно дифференцируемы на интервале (а;b).
f ( x )
Тогда если функциональный ряд
равномерно
n 1
n
сходится на отрезке [a; b], то сумма S(x) исходного ряда
имеет на интервале (а;b) производную, причем
f n ( x) S ( x) f n ( x)
n 1
n 1
4) Если все члены равномерно сходящегося на отрезке
[a; b] ряда умножить на ограниченную
на этом отрезке
функцию φ(х), то полученный ряд ( x) f n ( x) также
n 1
будет равномерно сходящимся на отрезке [a; b] .

12.

Степенной рад

13.

Степенной ряд
- функциональный ряд вида a ( x x )
n
n 0
n
0
a0 a1 ( x x0 ) a2 ( x x0 ) ... an ( x x0 ) ...
2
n
где {an} – бесконечная числовая последовательность,
члены которой называют коэффициентами степенного
ряда, т.е. членами ряда являются степенные функции с
целыми показателями степеней аргумента х,
.
При х0=0
n
a
x
n
n 0
Свободный член а0 ряда считают нулевым членом ряда
Область сходимости степенного ряда содержит по крайней
мере одну точку х=х0

14.

n
a
x
n
Теорема Абеля
n 0
1) Если степенной ряд сходится при некотором значении
х=α≠0, то он абсолютно сходится при всяком значении х,
для которого справедливо неравенство x
2) Если степенной ряд расходится при некотором
значении х=β, то он расходится при всяком х, для
которого справедливо неравенство x
сходится
расходится
-|β|
-|α|
0
|α|
|β|
расходится
Нильс Хе́нрик А́бель (5.08.1802 - 6.04.1829) —
норвежский математик. В 2002 г.
правительство Норвегии учредило Абелевскую
премию по математике.

15.

n
a
x
n
Теорема Абеля
абсолютно сходится
n 0
1) Если степенной ряд сходится при некотором
значении х=α≠0, то он абсолютно сходится при
всяком значении х, для которого справедливо
неравенство x
Доказательство:
M 0 : n N
a сходится
n 0
a n n M ограничена
lim an n 0
n
n
n
n
n
x
x
n x
an x an an M
n
x
n
n
x
1
M
n 0
x
n
сходится
n
a
x
n сходится
n 0

16.

n
a
x
n
Радиус и интервал сходимости ряда n 0
Число R>0, называется радиусом сходимости ряда, если оно
обладает следующими свойствами:
при |x|<R ряд сходится абсолютно,
при |x|>R ряд расходится.
Интервал (-R; R) называют интервалом сходимости данного
ряда, т.е. для всякой точки х, лежащей внутри этого
интервала, ряд сходится при том абсолютно
–R
0
R

17.

Радиус и интервал сходимости ряда
x0 R; x0 R
n
a
(
x
x
)
n
0
n 0
сходится
расходится
x0 – R
x0
расходится
x0 +R
Если R = 0, то область (интервал) сходимости ряда
х=х0
Если R =∞, то область (интервал) сходимости ряда
(- ∞; +∞)
an
R lim
n a
n 1
R lim
n n
1
| an |

18.

Степенной ряд
n
a
x
n
n 0
Для всякого степенного ряда с действительными
коэффициентами существует радиус сходимости R.
Степенной ряд сходится равномерно (или
мажорируем) на любом отрезке [–r ; r], целиком
лежащем внутри интервала сходимости (–R ; R).
–R
–r
0
r
R
Степенные ряды обладают всеми свойствами равномерно сходящихся рядов

19.

Свойства степенных рядов
1. Сумма степенного ряда S(x) является непрерывной
функцией в каждой точке интервала сходимости.
2. Степенные ряды
n
a
x
n
n
b
x
n
и n 0
, имеющие радиусы
сходимости соответственно R1 и R2, можно почленно
складывать, вычитать и умножать. Радиус сходимости
произведения, суммы и разности рядов будет
n 0
R min R1 ; R2

20.

Свойства степенных рядов
n
a
x
n
n 0
3. Степенной ряд можно почленно интегрировать на
любом отрезке [0; x] расположенном внутри его
интервала сходимости x R; R
x
a n 1 n
a1 2
n
an x dx a0 x x ...
x ...
0
2
n
n 0
В результате получаем степенной ряд, имеющий тот же
радиус сходимости, что и исходный.
4. Степенной ряд можно почленно дифференцировать
внутри интервала сходимости. Степенной ряд
n 1
na
x
n
n 1
составленный из производных членов исходного ряда,
имеет тот же радиус сходимости, что и данный ряд.