Проецирование плоскостей

1.

ГАПОУ СО Уральский колледж строительства, архитектуры и
предпринимательства (УКСАП)
Екатеринбург 2022

2. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ПЛОСКОСТИ

• Плоскость – множество положений прямой
линии, пересекающей прямую, и проходящей
через точку пространства, расположенную
вне этой прямой.
A
a
Прямую в пространстве можно задать тремя точками, не лежащими на одной
прямой.

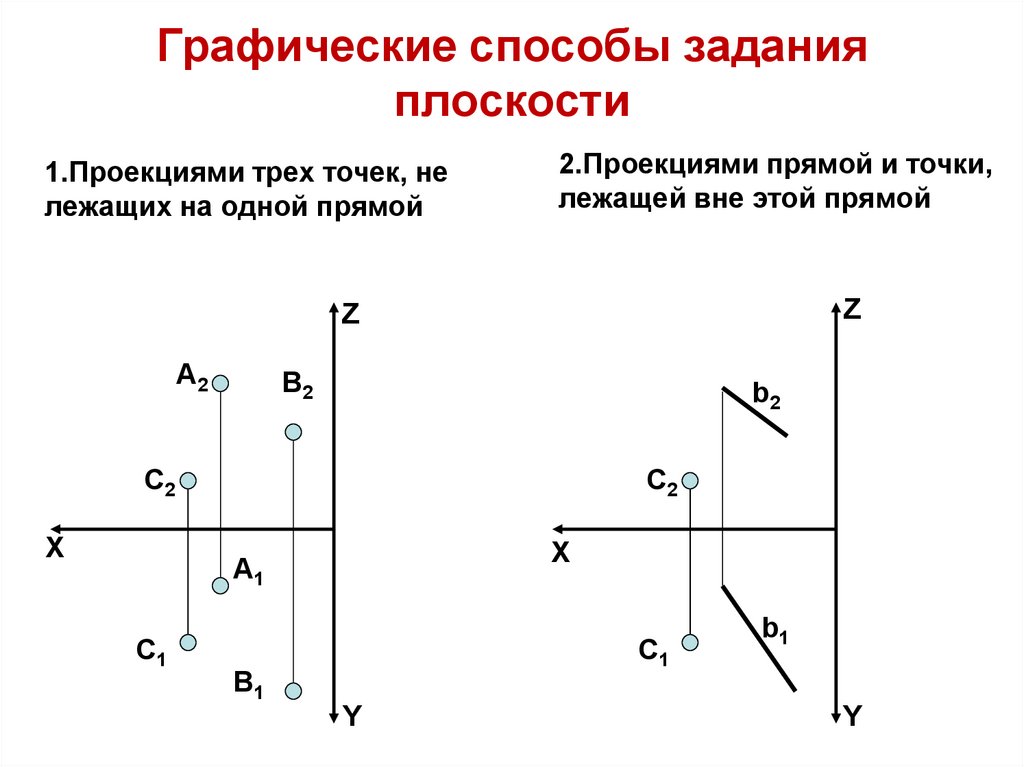
3. Графические способы задания плоскости

1.Проекциями трех точек, не
лежащих на одной прямой
2.Проекциями прямой и точки,
лежащей вне этой прямой
Z
Z
А2
В2
b2
C2
X
C2
X
А1
C1
C1
В1
Y
b1
Y

4.

Графические способы задания плоскости
3. Проекциями двух
параллельных прямых
4. Проекциями двух
пересекающихся прямых
Z
Z
a2
а2
X
К2
b2
b2
X
b1
a1
а1
b1
Y
К1
Y

5.

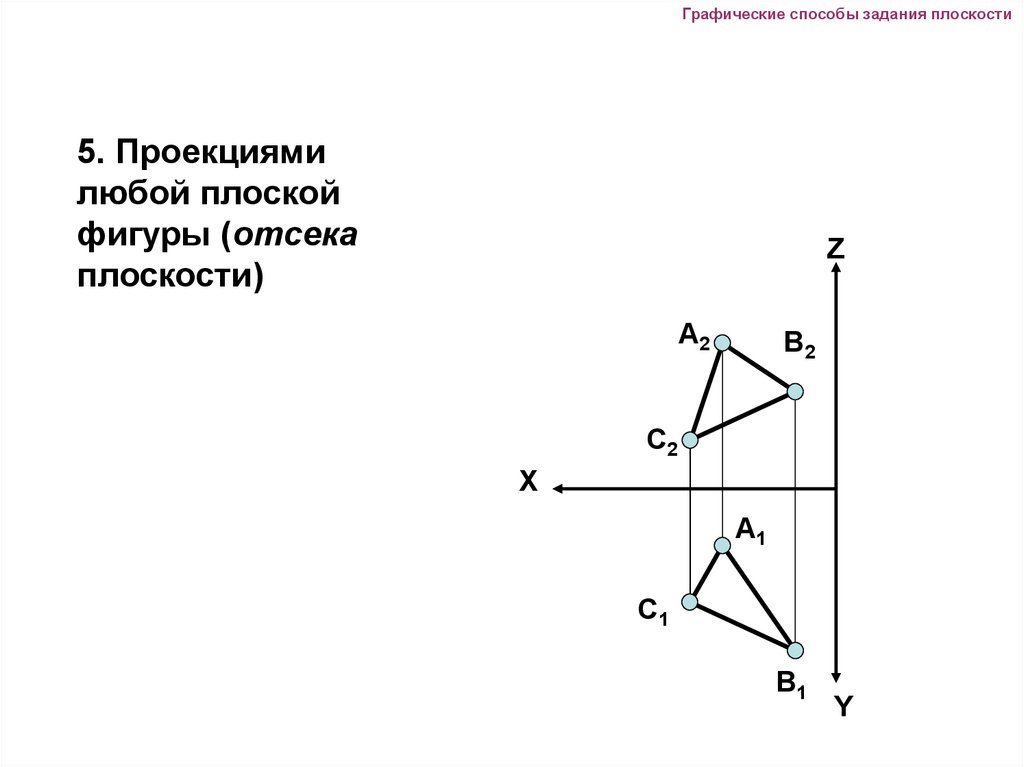
Графические способы задания плоскости
5. Проекциями
любой плоской
фигуры (отсека
плоскости)
Z
А2
В2
C2
X
А1
C1
В1
Y

6.

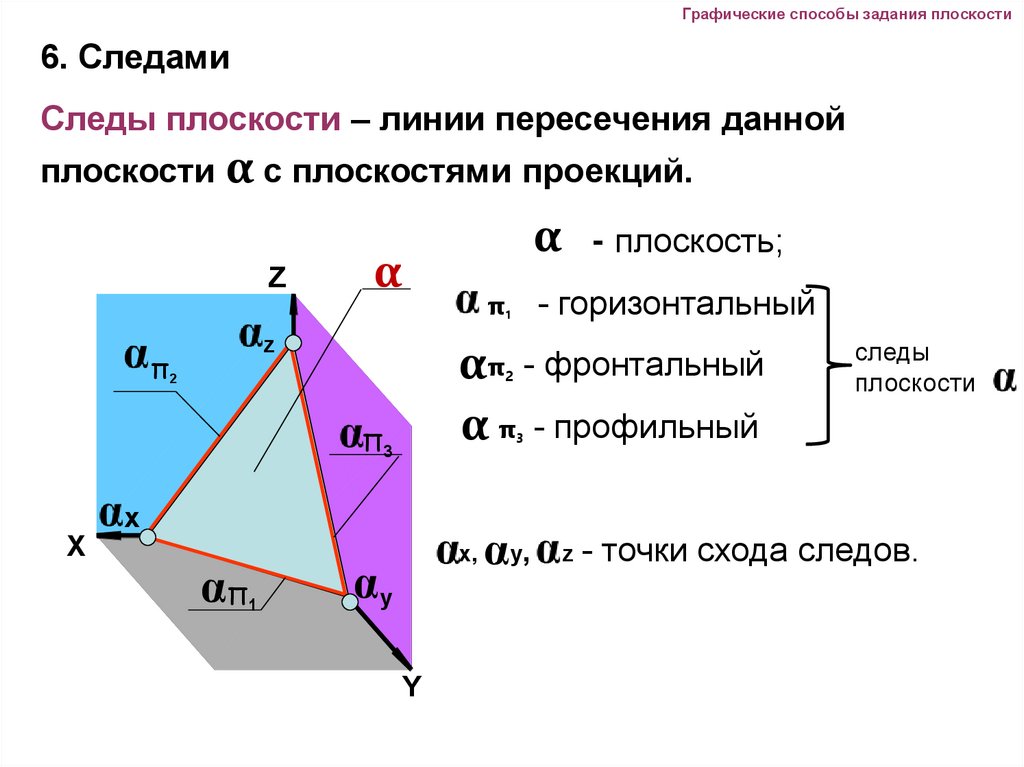
Графические способы задания плоскости
6. Следами
Следы плоскости – линии пересечения данной
плоскости α с плоскостями проекций.
Z
α - плоскость;
α
απ - фронтальный
α π - профильный
z
П2
- горизонтальный
π1
2
П3
3
x
X
x,
П1
следы
плоскости
y
Y
y,
z - точки схода следов.

7.

Графические способы задания плоскости
Задание плоскости следами на ортогональном чертеже
(
x,
y,
Z
z)
z
Z
X
х
Y
X
Y
y
Y

8. 2. ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ

По их расположению относительно плоскостей
проекций плоскости подразделяют на:
• плоскости частного положения
• плоскости общего положения
Плоскости частного положения разделяют на:
• Плоскости, параллельные плоскостям проекций,
– плоскости уровня
• Плоскости,
перпендикулярные
плоскостям
проекций, – проецирующие плоскости

9.

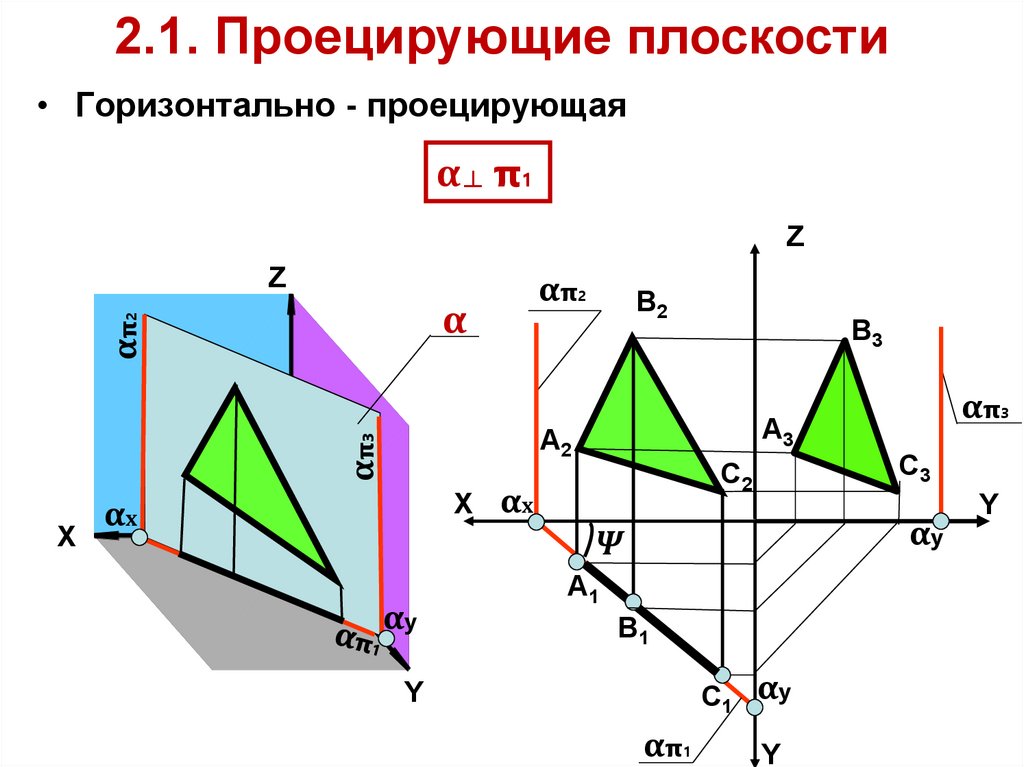
2.1. Проецирующие плоскости
• Горизонтально - проецирующая
α ┴ π1
Z
Z
απ2
α
В2
С2
X αх
αх
В3
А3
А2
απ3
X
απ 2
С3
αy
Ψ
αy
α π3
А1
В1
С 1 αy
Y
απ1
Y
Y

10.

Проецирующие плоскости
Свойство проецирующей плоскости собирать проекции
размещённых на ней объектов (точек, отрезков, плоских
фигур) на её характерном следе называется
собирательным.
Z
Z
απ 2
α
В2
В3
απ2
X
А3
А2
απ3
С2
X αх
αх
С3
αy
Ψ
А1
В1
αy
απ3
С 1 αy
Y
απ1
Y
Y

11.

• Фронтально-проецирующая
α ┴ π2
Z
απ 2
Z
α
С2
αz
α π2
αx
А2
С3
В3
φ
А1
Y
απ 3
В2
αx
απ 1
X
X
αz
А3
С1
В1
Y
Y

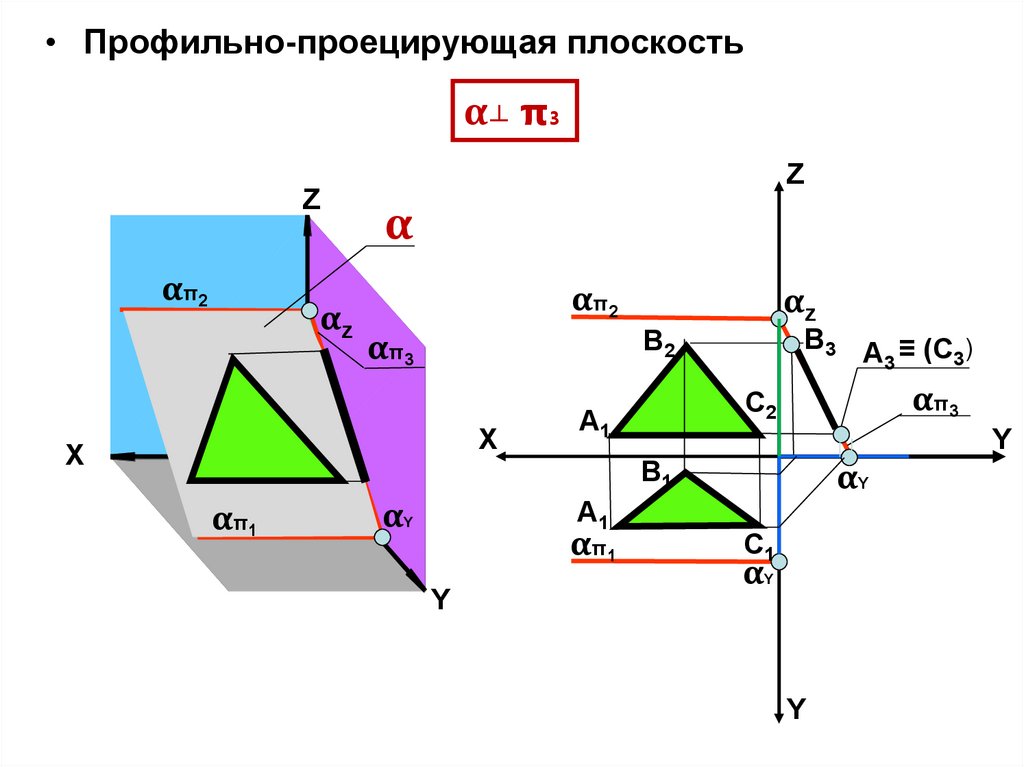
12.

• Профильно-проецирующая плоскость
α ┴ π3
Z
απ 2
αz
Z
α
απ2
αz
В3 А ≡ (C )
3
3
В2
απ 3
X
X
απ 3
С2
А1
Y
В1
απ 1
αY
А1
απ 1
Y
αY
С1
αY
Y

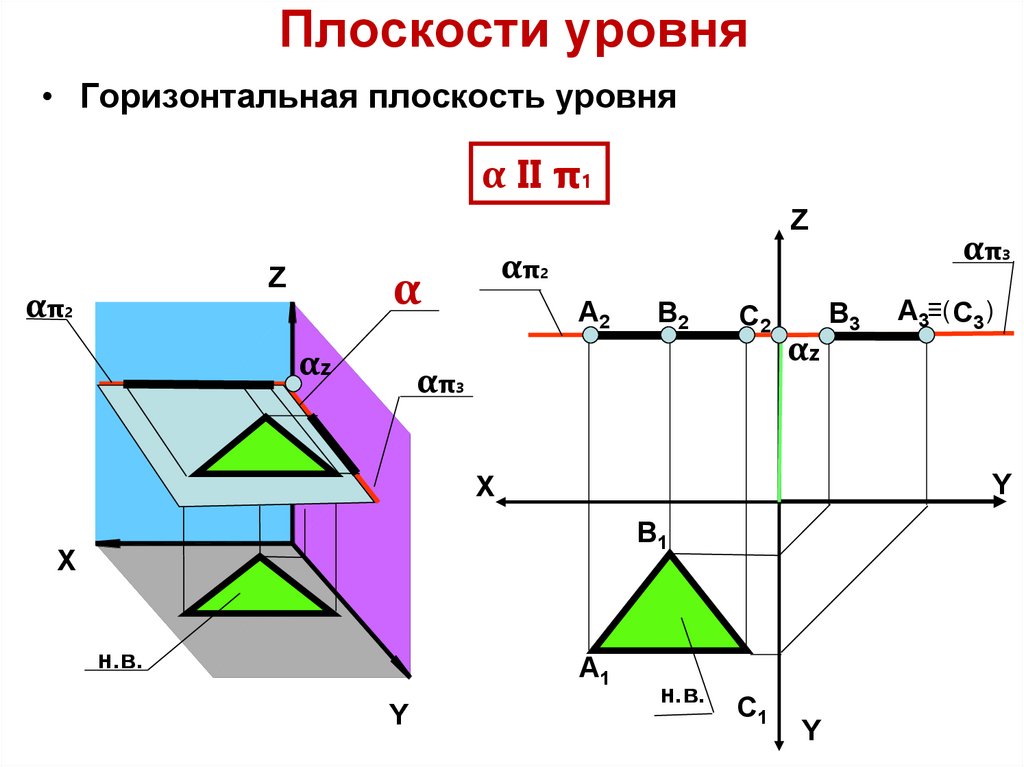
13. Плоскости уровня

• Горизонтальная плоскость уровня
α II π1
απ2
Поскольку плоскость α
α
Z
αz
параллельна плоскости π1, по
отношению к плоскостям π2 и
α π3
π3
X
X
н.в.
Y
она перпендикулярна и
обладает собирательным
свойством.

14. Плоскости уровня

• Горизонтальная плоскость уровня
α II π1
Z
απ2
απ2
α
Z
αz
А2
В2
С2
α π3
αz
В1
X
А1
Y
В3
А3≡( С3 )
Y
X
н.в.
απ3
н.в.
С1
Y

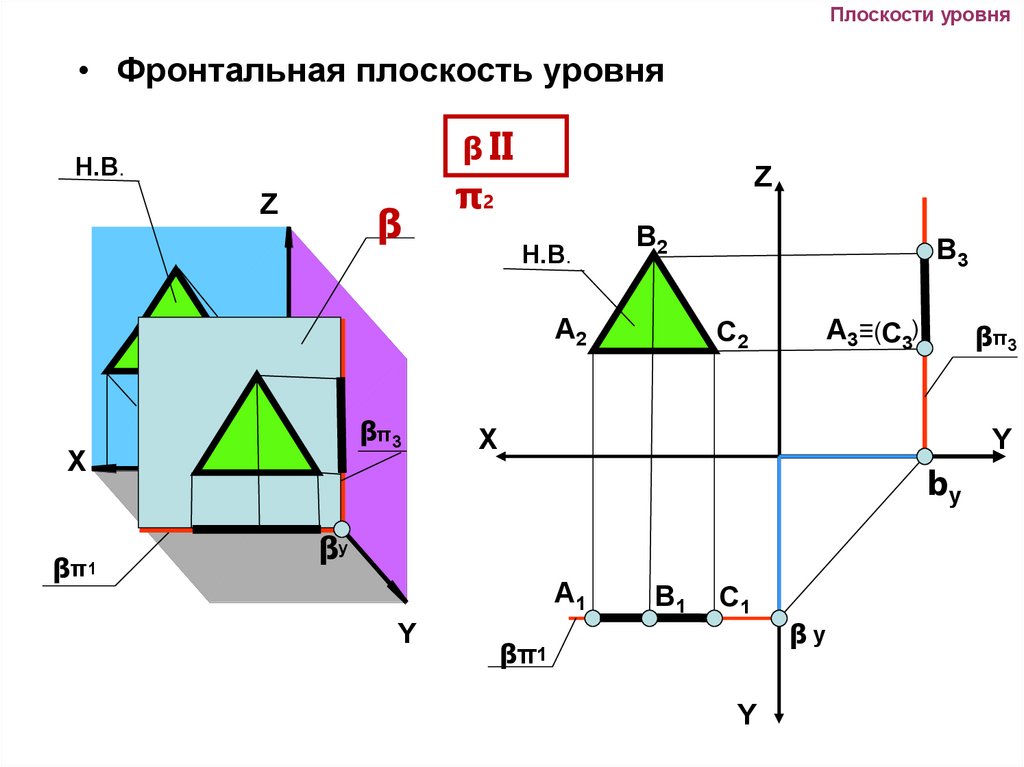
15.

Плоскости уровня
• Фронтальная плоскость уровня
ꞵ II
Н.В.
Z
ꞵ
Z
π2
Н.В.
В2
А2
ꞵπ3
X
ꞵπ1
В3
А3 ≡(С3)
С2
ꞵπ3
X
Y
by
ꞵy
А1
Y
В1
С1
ꞵπ1
Y
ꞵy

16.

Плоскости уровня
• Профильная плоскость уровня
II
π3
Z
Z
π2
π2
B3
B2
Н.В.
Н.В.
x
X
A2
C2
x
A3
C3
X
A1
B1
π1
Y
C1
π1
Y
Y

17. ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ

• Плоскость общего положения не параллельна и не
перпендикулярна ни одной из плоскостей проекций.
Z
απ2
αz
α
απ3
αx
X
απ1
αy
Y

18.

ПРИНАДЛЕЖНОСТЬ ТОЧКИ И ПРЯМОЙ
ПЛОСКОСТИ
1. Точка принадлежит плоскости, если она принадлежит
прямой, лежащей в этой плоскости
2. Прямая принадлежит плоскости, если она проходит:
а) через две точки этой плоскости;
б) через точку плоскости параллельно какой-либо
прямой этой плоскости

19.

Задача. Дано: α(αх, αy); αx(x, 0, 0); A(x, y, z)
Принадлежит ли точка А плоскости α?
Z
X
απ 2
Вывод:
А2
Точка А не принадлежит
плоскости α.
αx
А1
απ 1
Y

20. ОСОБЫЕ ЛИНИИ ПЛОСКОСТИ

ЛИНИИ
УРОВНЯ
ПЛОСКОСТИ
–
линии,
параллельные
плоскостям
проекций
и
принадлежащие данной плоскости;
2. ЛИНИИ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИ
– линии, определяющие угол наклона данной
плоскости к одной из плоскостей проекций.
ЛНН перпендикулярны линиям уровня:
• горизонтали плоскости;
• фронтали плоскости.
1.

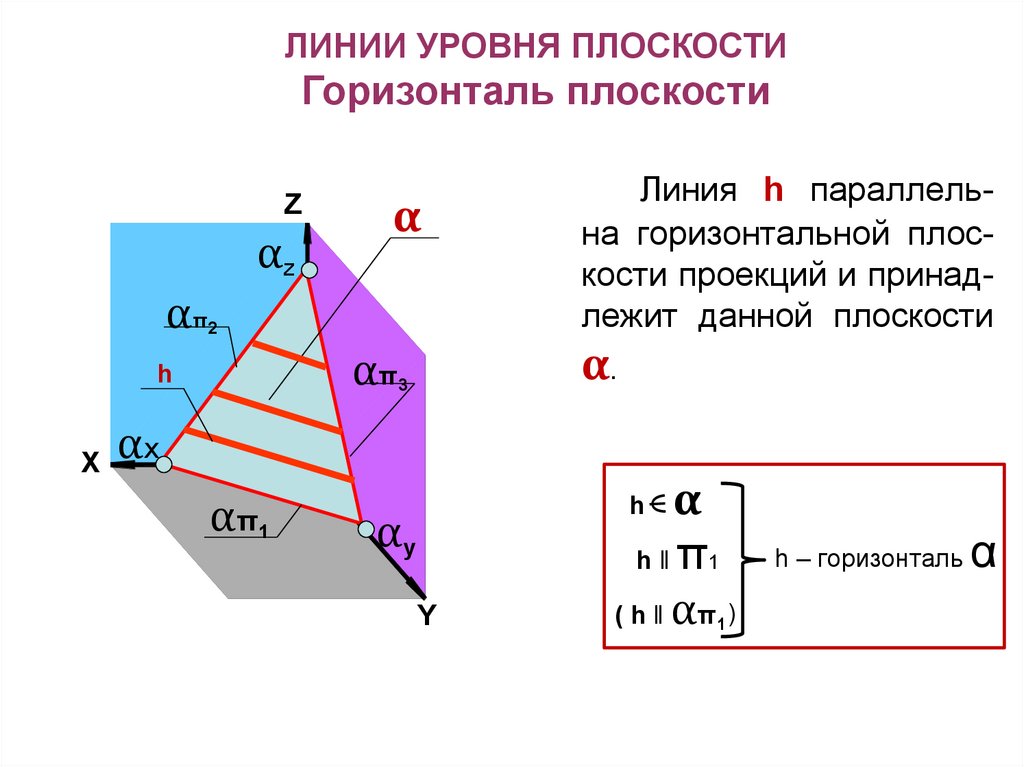
21.

ЛИНИИ УРОВНЯ ПЛОСКОСТИ
Горизонталь плоскости
Z
αz
απ
2
απ
h
X
α
Линия h параллельна горизонтальной плоскости проекций и принадлежит данной плоскости
α.
3
αx
απ1
α
h ‖ π1
( h ‖ απ )
h
αy
Y
1
h – горизонталь
α

22.

ЛИНИИ УРОВНЯ ПЛОСКОСТИ
Горизонталь плоскости,
заданной следами
Z
απ
2
H2
X
А2
h2
αx
H1
απ1
αz
h1
А1
αy
Y
α
AH ‖ π1
(AH ‖ απ )
AH
1
AH – горизонталь
α

23.

ЛИНИИ УРОВНЯ ПЛОСКОСТИ
Горизонталь плоскости
треугольника
В2
Линия AH параллельна
горизонтальной
плоскости
проекций
и
принадлежит плоскости
ΔАВС.
H2
А2
С2
X
А1
AH
AH ‖
С1
H1
В1
АВС
π1
AH – горизонталь
АВС

24.

Фронталь плоскости
Z
απ 2
α
αz
ЛИНИИ УРОВНЯ ПЛОСКОСТИ
Линия f параллельна
фронтальной
плоскости
проекций и принадлежит
данной плоскости α .
απ 3
ax
X
απ 1
α
f ‖ π2
( f ‖ απ )
f
f
ay
Y
2
f – фронталь
α

25.

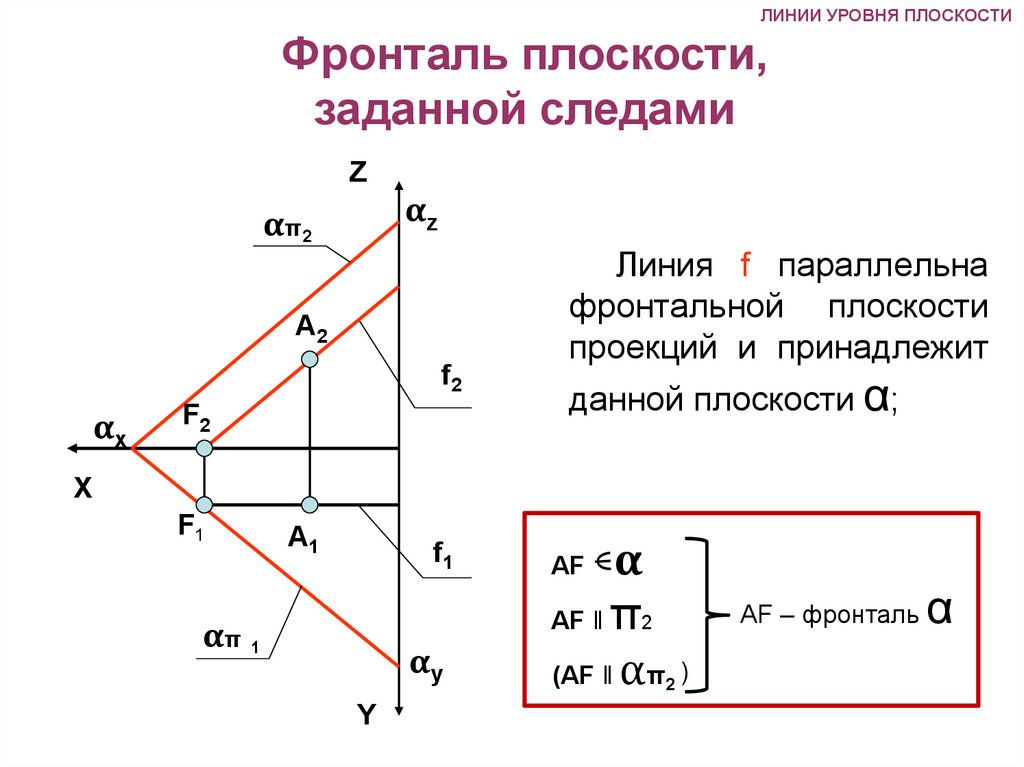
ЛИНИИ УРОВНЯ ПЛОСКОСТИ
Фронталь плоскости,
заданной следами
Z
αz
απ 2
A2
f2
αx
F2
Линия f параллельна
фронтальной плоскости
проекций и принадлежит
данной плоскости α;
X
F1
A1
f1
απ 1
αy
Y
α
AF ‖ π2
(AF ‖ απ )
AF
2
AF – фронталь
α

26.

ЛИНИИ УРОВНЯ ПЛОСКОСТИ
Фронталь плоскости
В2
F2
А2
С2
X
А1
С1
F1
В1
Линия f параллельна фронтальной плоскости проекций и принадлежит данной плоскости ΔАВС.

27.

ЛИНИИ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИ
К ПЛОСКОСТЯМ ПРОЕКЦИЙ
Линия наибольшего наклона плоскости α к
горизонтальной плоскости проекций
Z
απ2
h
X
α
Линия наибольшего наклона
плоскости α к горизонтальной
плоскости проекций (линия
ската
плоскости
α)
перпендикулярна горизонтали h
плоскости α и горизонтальному
следу плоскости.
αz
k
απ3
απ1
αy
αx
k ┴ απ1
Y
k ┴h
k – лнн α к π1
(линия ската)

28.

ЛИНИЯ НАИБОЛЬШЕГО НАКЛОНА
плоскости α к горизонтальной плоскости
проекций
αz
α π2
А2
H2
X
h2
αx
H1 D2
А1
απ 1
h1
D1
αy
Y
Линия наибольшего
наклона плоскости α к
горизонтальной плоскости
проекций (линия ската
плоскости α)
перпендикулярна
горизонтали h плоскости α
на π1 и горизонтальному
следу плоскости.
АD ┴ απ1
АD – лнн α к π1
(линия ската)
АD ┴ АН

29.

ЛИНИЯ НАИБОЛЬШЕГО НАКЛОНА
плоскости ΔАВС к горизонтальной плоскости
проекций
В2
ВD ┴ АH – линия ската
H2
А2
D2
С2
X
А1
D1
С1
С1
H1
В1

30.

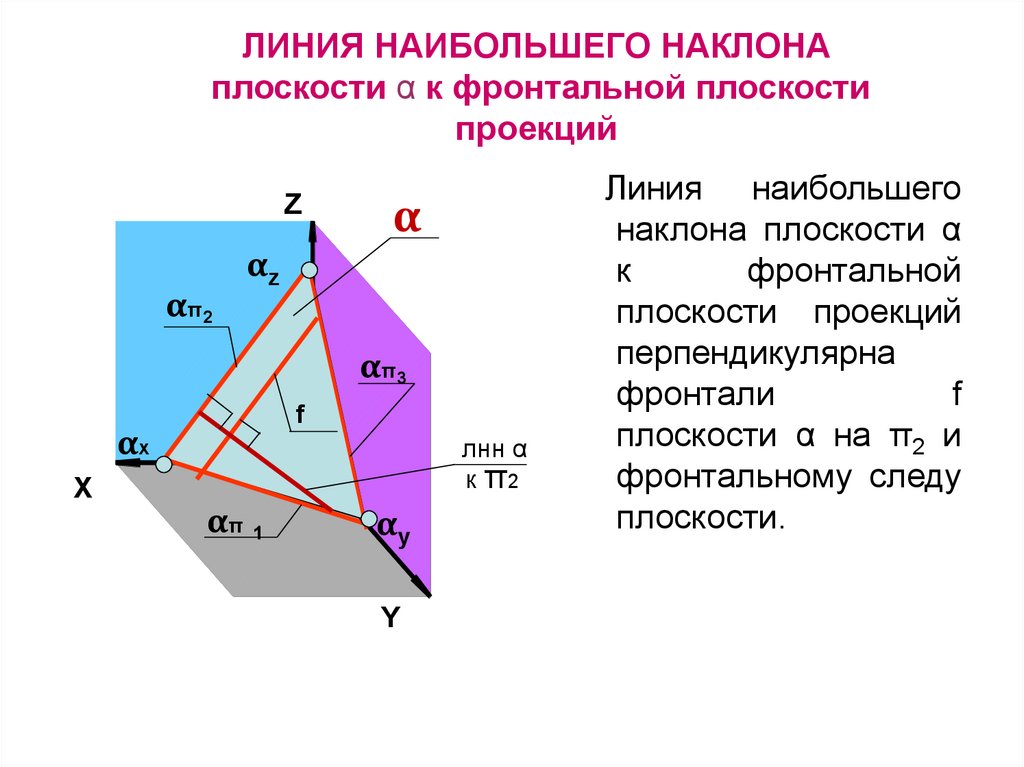
ЛИНИЯ НАИБОЛЬШЕГО НАКЛОНА
плоскости α к фронтальной плоскости
проекций
Z
απ 2
α
αz
απ 3
f
αx
X
лнн α
к π2
απ 1
αy
Y
Линия наибольшего
наклона плоскости α
к
фронтальной
плоскости проекций
перпендикулярна
фронтали
f
плоскости α на π2 и
фронтальному следу
плоскости.

31.

ЛИНИЯ НАИБОЛЬШЕГО НАКЛОНА
плоскости α к фронтальной плоскости проекций
Z
αz
απ 2
К2
A2
αx
F2
f2
К1
X
F1
A1
f1
απ 1
αy
Y
1. Линия наибольшего
наклона плоскости α к
фронтальной плоскости
проекций перпендикулярна
фронтали f плоскости α и
фронтальному следу
плоскости α .
2. АК ┴ АF
( А2К2 ┴ А2F2
А2К2 ┴ απ2)
АК – лнн α
к π2

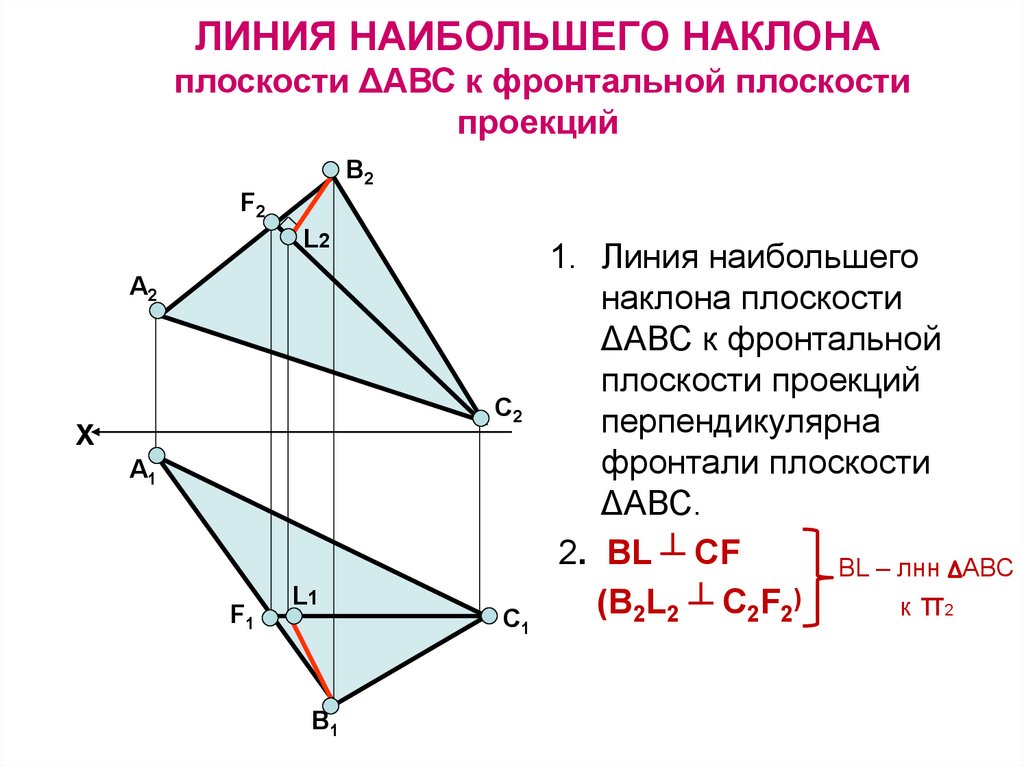
32.

ЛИНИЯ НАИБОЛЬШЕГО НАКЛОНА
плоскости ΔАВС к фронтальной плоскости
проекций
В2
F2
L2
А2
С2
X
А1
F1
L1
В1
С1
1. Линия наибольшего
наклона плоскости
ΔАВС к фронтальной
плоскости проекций
перпендикулярна
фронтали плоскости
ΔАВС.
2. ВL ┴ CF
BL – лнн АВС
(В2L2 ┴ C2F2)
к π2