Похожие презентации:
Методика моделирования дискретных и непрерывных случайных величин. Лекция 3
1.
Лекция 3.Методика моделирования дискретных
и непрерывных случайных величин
УЧЕБНЫЕ ВОПРОСЫ
1. Моделирование дискретных случайных величин.
2. Моделирование непрерывных случайных величин.
2.
Вопрос 1.Моделирование дискретных случайных
величин
1.1. Алгоритм моделирования дискретной случайной величины
3.
Допустим,что
нам
нужно
получить
значения случайной величины (СВ) ξ со
следующим распределением:
1 2 n
p1 p 2 p n
n
pi 1
i 1
(1.1)
4.
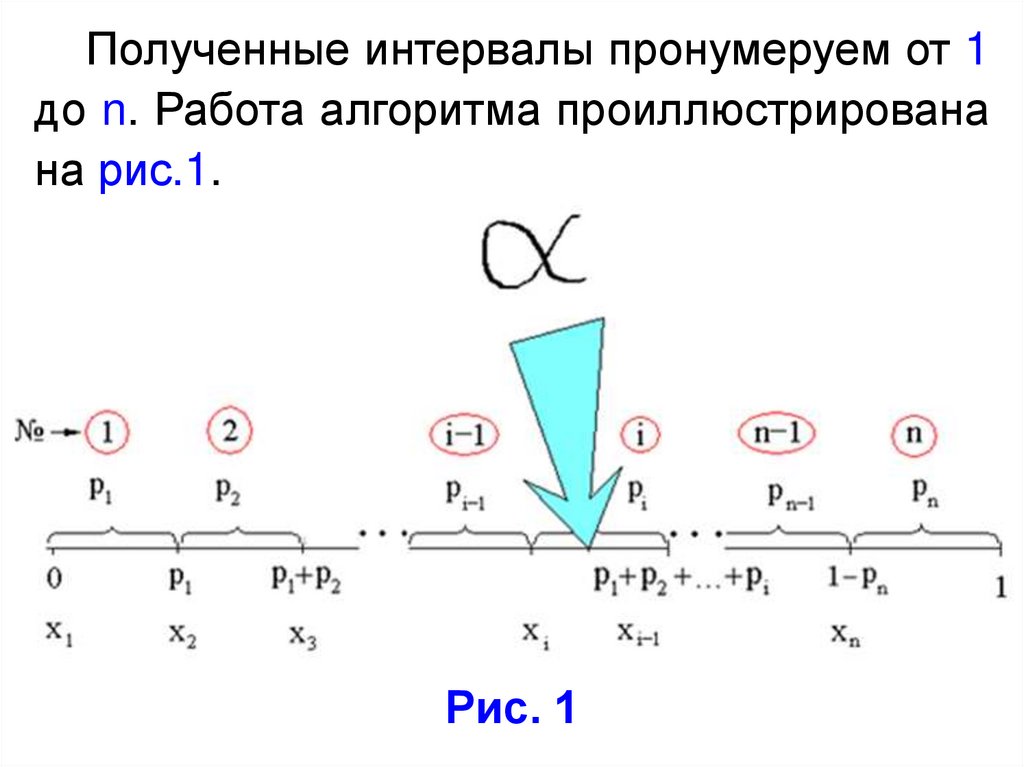
Разобьем отрезок [0;1] на n интервалов,длины которых равны соответственно:
p1, p2, …, pn.
Координатами точек
величины:
x1 = 0;
x2 = p1;
x3 = p1 + p2;
деления
…
xn = p1 + p2 + … + pn –1.
будут
5.
Полученные интервалы пронумеруем от 1до n. Работа алгоритма проиллюстрирована
на рис.1.
Рис. 1
6.
Рис. 27.
Для получения значения дискретной СВ(ДСВ) ξ необходимо выбрать значение БСВ
α и построить точку x = α.
Номер интервала i, в который попадет
БСВ α, определит значение ДСВ в данном
опыте: ξ = ξi.
8.
Так как БСВ α равномерно распределенав полуинтервале [0,1), то вероятность того,
что α окажется в некотором его отрезке,
равна длине этого отрезка. Значит,
P 0 p1 p1
P p1 p1 p 2 p 2
P p1 p 2 p n 1 1 p n
(1.2)
9.
Согласно нашей процедуре ξ = ξi тогда,когда выполняется неравенство:
p1 p 2 pi 1 p1 p 2 pi
(1.3)
В правой части строгое неравенство,
т.к. правая граница последнего отрезка
равна 1, а БСВ α<1.
Для
моделирования
последовательности ДСВ необходимо
повторить алгоритм несколько раз.
10.
1.2. Моделированиеслучайных событий
полной
группы
Определение. Совокупность событий
называется полной группой случайных
событий, если:
а) происходит хотя бы одно событие из
группы;
б) совместное наступление двух и более
событий из группы невозможно;
в) события группы имеют ненулевые
вероятности своего наступления.
11.
Пример.В случайном эксперименте по бросанию
монеты полную группу образуют два
события:
А1 – "выпадение орла";
А2 – "выпадение решки".
12.
1.3. Моделирование процесса случайного блуждания13.
Пусть ξt – случайныйдискретным временем
процесс
с
τ = m·Δt (m = 0,1,…)
и дискретным
состояний X:
фазовым
пространством
X x k x
где k = {-1; 0; 1};
Δt>0 – шаг дискретизации времени;
Δx>0 – шаг
пространства.
дискретизации
фазового
14.
Пусть в момент времени t≥0 процесснаходится в состоянии x, т.е. ξt=x, а в
следующий момент времени t+Δt состояние
процесса определяется соотношениями:
x x c вероятностью P
t t x x с вероятностью P_
x c вероятностью (1 P P_ )
(1.4)
Такой процесс называется процессом
случайного блуждания на прямой.
15.
Согласно (1.4) можно записать:t t x t
(1.5)
t x; 0; x – ДСВ с распределением вероятностей
P t x P_
P t 0 1 P P_
P x P
t
(1.6)
16.
Тогдасводится
моделирование
к
процесса
моделированию
в
ξt
каждый
момент времени t+Δt реализации СВ ηt и
использованию соотношения (1.5).
17.
Вопрос 2.Моделирование непрерывных случайных
величин
2.1. Метод обратной функции
18.
При построении имитационной моделисложной
системы
часто
необходимо
моделировать непрерывную СВ (НСВ) с
заданной
плотностью
распределения
вероятностей.
Например, интервалы времени между
моментами поступления заявок в СМО,
время обслуживания и т.п.
19.
Внекоторых
случаях
для
решения
данных задач применяют метод обратной
функции.
Рассмотрим
функцию
распределения
случайной величины:
x
y F x f x dx
(2.1)
20.
Обозначимчерез
x=F-1(y)
функцию,
обратную функции F(x).
Теорема.
Если α – базовая случайная величина, то
случайная
величина
ξ=F-1(α)
имеет
заданную плотность распределения fξ(x).
21.
Моделирующий алгоритм, реализующийметод
обратной
функции,
включает
следующие этапы:
1) нахождение функции распределения
F(x) по заданной плотности распределения
f(x) согласно (2.1);
2) нахождение обратной функции F-1(y);
3) моделирование реализации БСВ α и
вычисление СВ ξ по формуле ξ=F-1(α).
22.
Пример 1.Дана
плотность
экспоненциального
распределения:
0, если х 0
f ( х ) x
e , если х 0
23.
1) Определяем функцию экспоненциального распределения:x
x
0
0
F x f x dx e
x
dx
1 x x
x
e
1 e
0
(2.2)
2) Определяем обратную функцию:
1
x F y ln 1 y
1
(2.3)
24.
3) Для моделирования экспоненциальнораспределенной СВ ξ используем формулу:1
ln 1
(2.4)
где α – базовая случайная величина.
Так как величины α и 1-α одинаково
распределены, то эквивалентно следующее:
1
ln .
25.
Пример 2.Дана плотность равномерного распределения:
1
, если х а, b
f ( х) b a
0, если х a, b
(2.5)
26.
f(x)1
b a
a
b
Рис. 3
x
27.
1) Определяем функцию равномерногораспределения:
x
x
1
F x f x dx
dx
b a
x x a
1
x
b a a b a
(2.6)
28.
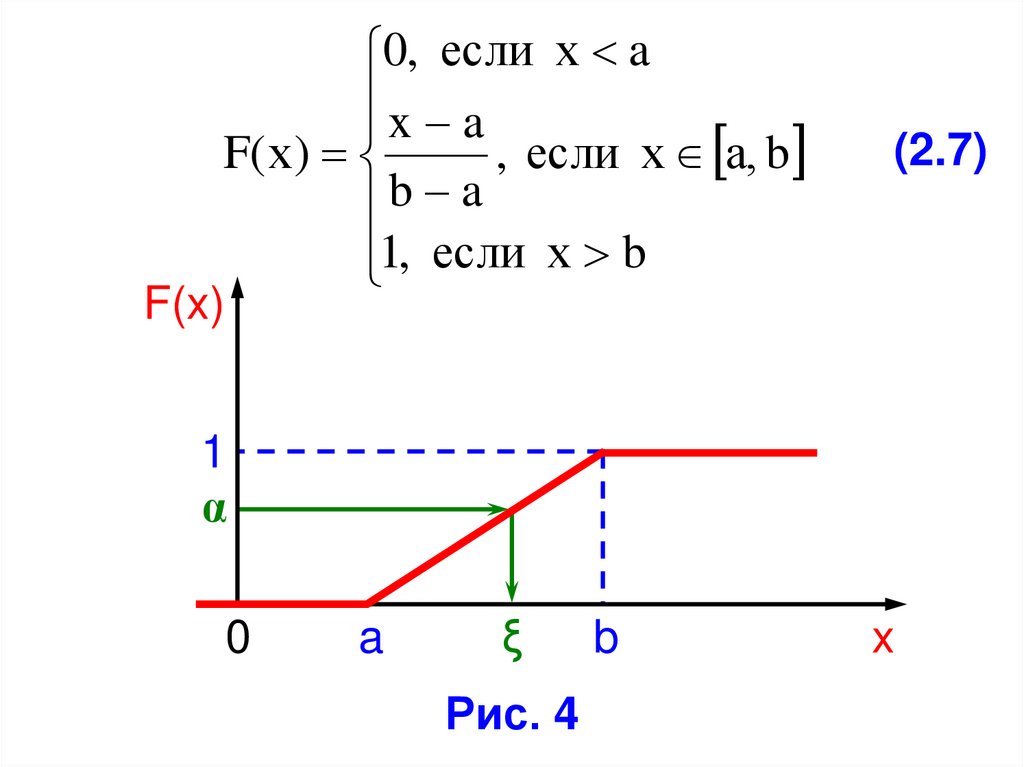
0, если х ax a
F( х )
, если х а, b
b a
1, если х b
(2.7)
F(x)
1
α
0
a
ξ
Рис. 4
b
x
29.
2) Определяем обратную функцию:x F
3) Для
1
y a y b a
моделирования
(2.8)
равномерно-
распределенной СВ ξ используем формулу:
a b a
где α – базовая случайная величина.
(2.9)
30.
2.2. Метод исключенияИспользуется
в
тех
случаях,
когда
плотность распределения f(x) моделируемой
СВ ξ имеет сложный аналитический вид.
31.
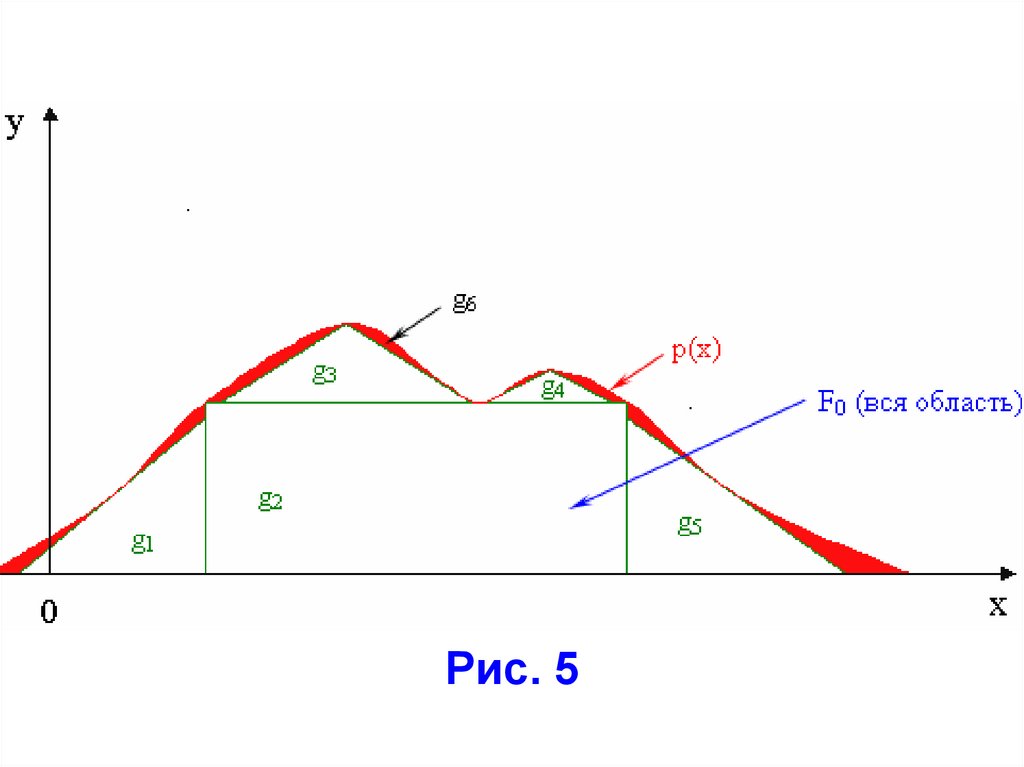
уg(x)
G
F0
p(x)
х
0
Рис. 5
32.
Обозначим: F0 = { (x,y); 0≤y≤p(x) } – область,ограниченную кривой y=p(x) и осью абсцисс
(рис. 5).
Определим мажорантную (огибающую)
функцию:
y=g(x); g(x)≥p(x)≥0
и область G = { (x,y); 0≤y≤g(x) }.
33.
ОбластьG
охватывает
(мажорирует)
область F0.
Функция g(x) должна иметь значительно
более простой, чем p(x)
аналитический
вид,
легко
моделировать
(ξ,η),
равномерно
позволяющий
случайный
вектор
распределенный в области G (например,
методом обратной функции).
34.
Моделирующийалгоритм
включает
следующие этапы:
1) подбор мажорантной функции g(x) для
заданной p(х);
2) моделирование
(ξ,η),
равномерно
области G;
случайного
вектора
распределенного
в
35.
3) проведение следующей процедуры:если (х,у) – реализация вектора (ξ,η) и
у≤p(х) (т.е. точка (х,у) попадает в область
F0),
то
х
принимается
в
качестве
реализации СВ ξ;
если у>p(х) (точка (х,у) – за пределами F0),
то реализация (х,у) исключается.
36.
Повторяяполучаем
алгоритм
требуемое
случайной величины ξ.
число
многократно,
реализаций
37.
2.3. Метод суперпозиции (композиции)При достаточно сложном виде функции
p(x) моделирование равномерного распределения в области F0 трудноосуществимо.
В этом случае F0 разбивается на простые
области,
моделирование
равномерного
распределения в которых возможно (рис. 6).
38.
Приэтом
вероятности
попадания
в
области равны их площадям. Используя
данные вероятности, "разыгрывают" номер
области,
в
которой
и
осуществляется
моделирование реализации СВ ξ.
39.
Рис. 540.
На рис. 6 область F0 разбита на 5простых
областей,
шестая
–
ограничена
;
огибающей
и данными областями:
.
6
p x Pi p i x
i 1
5
p 6 x
p 0 x Pi p i x
i 1
P6
5
P6 1 Pi
i 1
(2.10)
41.
Для ускорения моделирования разбиениена области происходит так, чтобы части gi,
имеющие
(наибольшую
наибольшую
площадь
вероятность
Рi),
соответствовали наиболее просто и быстро
моделируемым плотностям p(х).
Остаточную
плотность
p6
моделировать методом исключения.
можно
42.
Этапы моделирующего алгоритма:1) разбиение
на
F0
геометрически
простые области;
2) моделирование
случайного
вектора
(ξ,η) с координатами (х,у), равномерно
распределенного
в
области
F0
соответственно в выделенных областях;
и
43.
3) разыгрываниеслучайного
значений
вектора
разыгрыванием
ДСВ
по
координат
аналогии
и
с
проверка
соответствия вероятности их попадания в ту
или иную область.








































 Математика
Математика








