Похожие презентации:
Касательная к графику функции. (10 класс)
1. Касательная к графику функции.
10 класс2. Касательная к графику функции
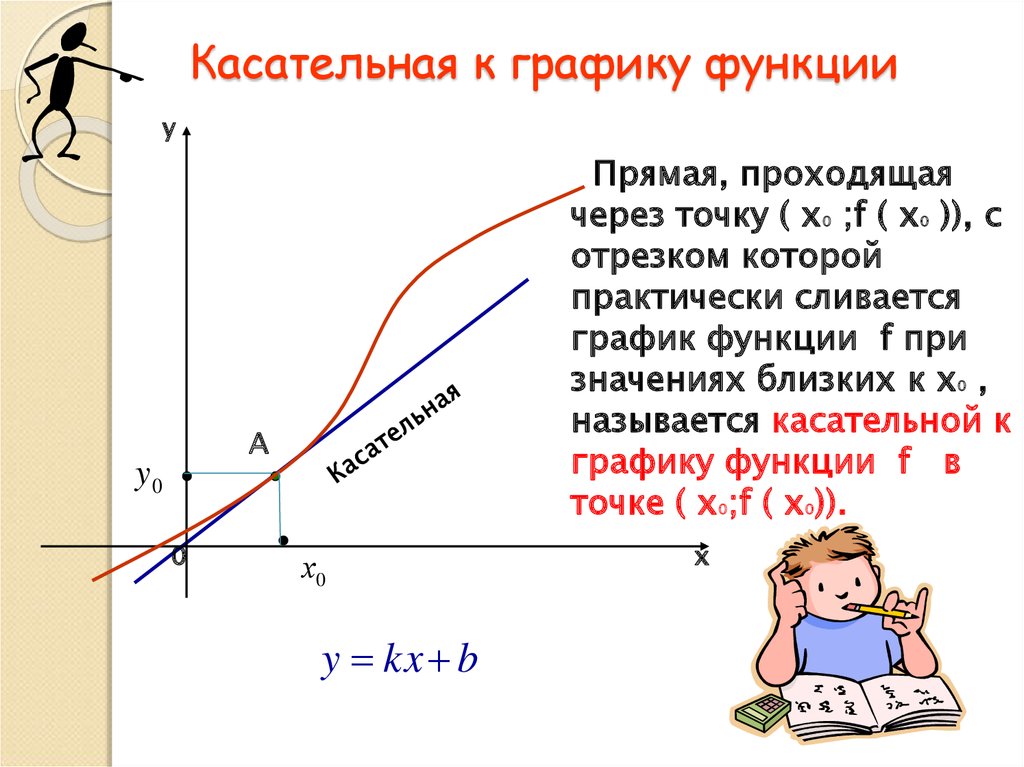
yПрямая, проходящая
через точку ( х0 ;f ( х0 )), с
отрезком которой
практически сливается
график функции f при
значениях близких к х0 ,
называется касательной к
графику функции f в
точке ( х0;f ( х0)).
A
y0
0
х0
y kx b
х
3. Касательная есть предельное положение секущей при ∆х→0
ytg k
x
y f (x)
Автоматический показ. Щелкните 1 раз.
y
Секущая
k – угловой
коэффициент
прямой(секущей)
y
х 0
k → f’(x0)
y
0
х0
х 0
х
х
х
Угловой коэффициент касательной равен f ˈ(х0). В этом состоит
геометрический смысл производной.
4. Касательная к графику дифференцируемой в точке хо функции f – это прямая, проходящая через точку (хо ; f(хо)) и имеющая угловой коэффициент fˈ(
Касательная к графику дифференцируемой в точке хофункции f – это прямая, проходящая через точку (хо ; f(хо)) и
имеющая угловой коэффициент fˈ(хо).
Выведем уравнение касательной к графику функции f
в точке А (хо; f(хо)).
y kx b
k = fˈ(хо) => y = fˈ(хо)•х + b
Найдем b :
f(хо) = fˈ(хо)•хо + b => b = f(хо) - fˈ(хо)•хо
y = fˈ(хо)•х + f(хо) - fˈ(хо)•хо
y = f(хо) – fˈ(хо)(х - хо)
5. Формула Лагранжа.
Если функция дифференцируема, то наинтервале (a;b) найдется такая точка с Є (a;b) ,что
f(b) –f(a)
f‘(с) =
b-a
y
f‘(c) = tg α
lo ll AB
lo
C
B
A
α
0
a
c
b
х




 Математика
Математика








