Похожие презентации:
Показатели надежности. Лекция 7
1.
Л7-1ЛЕКЦИЯ 7
Показатели надежности
2.
Л7-2Показатели надежности:
1) показатели безотказности
2) показатели ремонтопригодности
3) показатели долговечности
4) показатели сохраняемости
5) комплексные показатели надежности
3.
Л7-3Показатели надежности единичные:
1) показатели безотказности
2) показатели долговечности
3) показатели ремонтопригодности
4) показатели сохраняемости
Показатели надежности комплексные – это
показатели
готовности,
т.к.
они
характеризуют
одновременно несколько свойств надежности, как правило
это безотказность и ремонтопригодность
Существуют показатели надежности:
1) для невосстанавливаемых систем
2) для восстанавливаемых систем
4.
Л7-4Показатели безотказности
(для невосстанавливаемых систем)
Таблица 2.1
P(t) Вероятность безотказной работы
Q(t) Вероятность отказа
f(t) Плотность распределения наработки до отказа
λ(t) Интенсивность отказов
T
Средняя наработка до отказа
tγ
Гамма-процентная наработка до отказа
5.
Л7-5Вероятность безотказной работы системы
Время безотказной работы системы (или
наработка до отказа) – непрерывная случайная величина,
описываемая интегральной функцией распределения
F(t).
Вероятность безотказной работы P(t) есть
вероятность того, что в пределах заданной наработки
отказ системы не возникает:
P(t) = 1 – F(t)
6.
Л7-6Вероятность отказа Q(t)
есть вероятность того, что система откажет в течение
заданного времени работы (будучи работоспособной в
начальный момент времени):
Q(t) = F(t) = 1 – P(t)
В данном случае вероятность отказа Q(t) совпадает
с интегральной функцией распределения наработки до
отказа F(t).
7.
Л7-7Плотность распределения наработки до отказа f(t)
Для
мгновенных
значений
надежности
кроме
F(t)
дифференциальная
функция
–
распределения наработки до отказа f(t):
показателей
применяется
плотность
d
d
d
f (t ) F (t ) Q(t ) P(t )
dt
dt
dt
8.
Л7-8Интенсивность отказов λ(t)
[как и f(t)] является дифференциальной характеристикой
безотказности и есть условная плотность вероятности
возникновения отказа системы, определяемая для
рассматриваемого момента времени при условии, что до
этого момента отказ не возникал, т.е.
f (t )
(t )
P(t )
(2.1)
9.
Л7-9При
f (t )
d
P (t )
dt
1 d
1
d
(t )
P(t )
F (t )
P(t ) dt
1 F (t ) dt
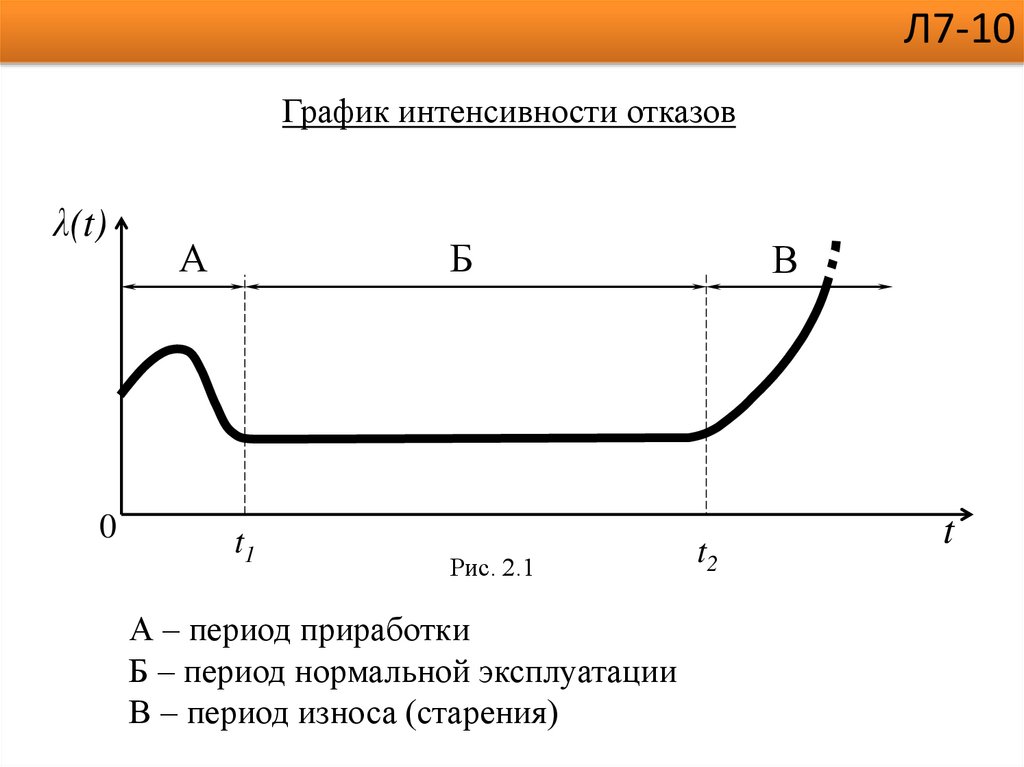
График интенсивности отказов см. на рисунке 2.1
10.
Л7-10График интенсивности отказов
λ(t)
0
А
Б
t1
Рис. 2.1
А – период приработки
Б – период нормальной эксплуатации
В – период износа (старения)
В
t2
t
11.
Л7-11Плотность вероятности f(t) и интенсивность отказов
λ(t) имеют размерность ч-1 (т.е. количество отказов за час
работы).
Значения f(t)[λ(t)] лежат в пределах 10-7 ÷ 10-8 ч-1
Для упрощения используют
1 фит = 10-9 ч-1
т.е. λ(t) = 10-8ч-1=10 фит
12.
Л7-12Средняя наработка до отказа T
есть математическое ожидание наработки
системы до первого отказа:
0
0
T t f (t )dt tdF (t )
[1 F (t )]dt P(t )dt
0
0
(2.2)
13.
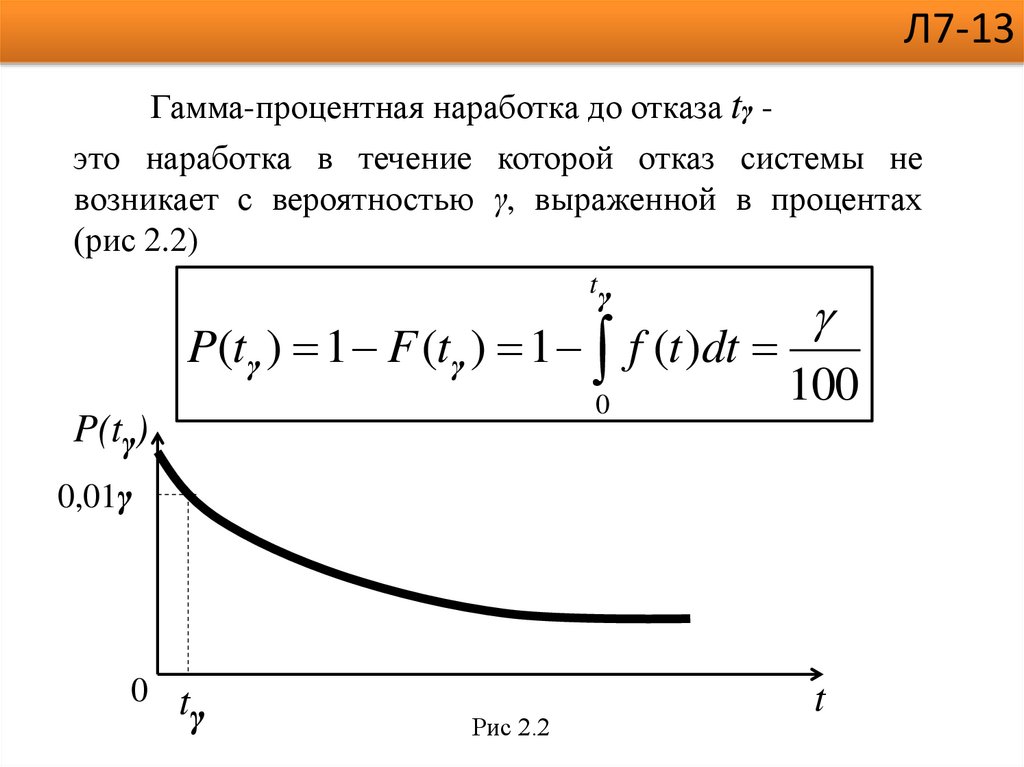
Л7-13Гамма-процентная наработка до отказа tγ это наработка в течение которой отказ системы не
возникает с вероятностью γ, выраженной в процентах
(рис 2.2)
tγ
P(tγ ) 1 F (tγ ) 1 f (t )dt
0
P(tγ)
100
0,01γ
0 t
γ
Рис 2.2
t
14.
Л7-14Физический смысл средней наработки до отказа T
Пусть вероятность безотказной работы P(t)=0,37.
Это означает, что при средней наработке системы
до отказа, например, при Т=1000 часов, вероятность
достижения наработки Т=1500 часов будет меньше 0,37
(т.е. P(t)<0,37).
15.
Л7-15Физический смысл гамма-процентной наработки до отказа tγ.
Например, при вероятности безотказной работы
P(tγ)=0,9 гамма-процентная наработка до отказа tγ в 10 раз
меньше средней наработки до отказа Т, при P(tγ)=0,99 – в 100
раз.
Это означает, что при T=1000 часов вероятность
P(tγ)=0,99 обеспечивается только на первых 10 часах работы
системы (т.е. из 100 изделий через 10 часов работы останутся
работоспособными 99, через 100 часов 90 и т.д.).













 Промышленность
Промышленность








