Решение неравенств второй степени с одной переменной

1.

Решение неравенств второй
степени с одной переменной

2.

Чтобы решить квадратичное неравенство
надо:
1.
2.
3.
4.
Рассмотреть функцию у=ах²+bх +с, определить
направление ветвей;
Найти нули функции, решив квадратное
уравнение ах²+bх+с=0;
Схематически построить параболу, учитывая
направление ветвей и точки пересечения с осью х;
Учитывая знак неравенства, выбрать нужные
промежутки и записать ответ.

3.

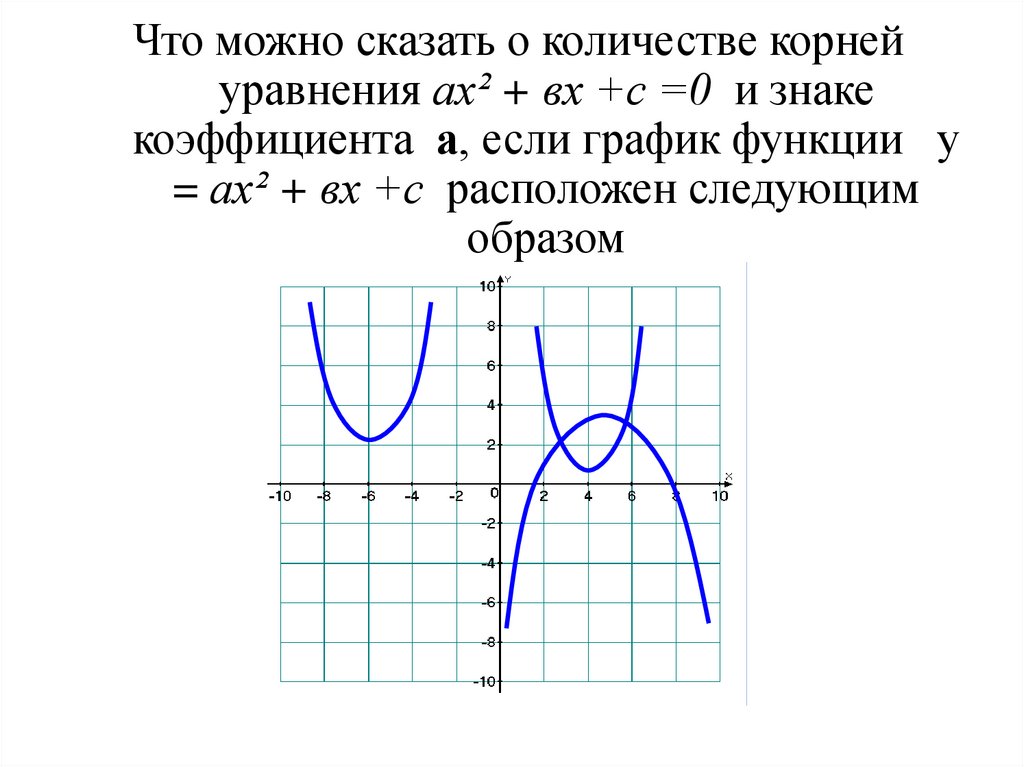
Что можно сказать о количестве корней
уравнения ах² + вх +с =0 и знаке
коэффициента а, если график функции у
= ах² + вх +с расположен следующим
образом

4.

Для решения неравенств вида ах²
+ вх +с >0 и ах² + вх +с < 0
поступают следующим образом:
• Находят дискриминант квадратного трехчлена и
выясняют, имеет ли трехчлен корни;
• Если трехчлен имеет корни, то отмечают их на оси х и
через отмеченные точки проводят схематически
параболу, ветви которой направлены вверх при а >0
или вниз при а < 0; если трехчлен не имеет корней, то
схематически изображают параболу, расположенную в
верхней полуплоскости при а >0 и в нижней при а < 0;
• Находят на оси х промежутки, для которых точки
параболы расположены выше оси х ( если решают
неравенство ах² + вх +с >0 или ниже оси х (если
решают неравенство ах² + вх +с < 0).

5.

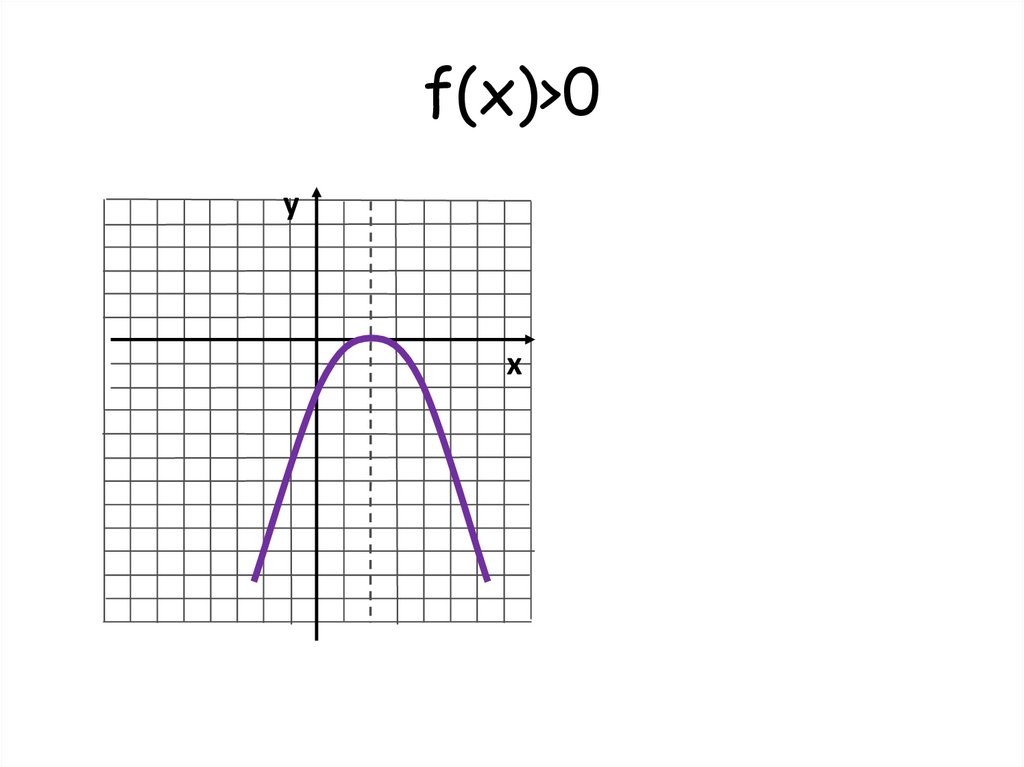
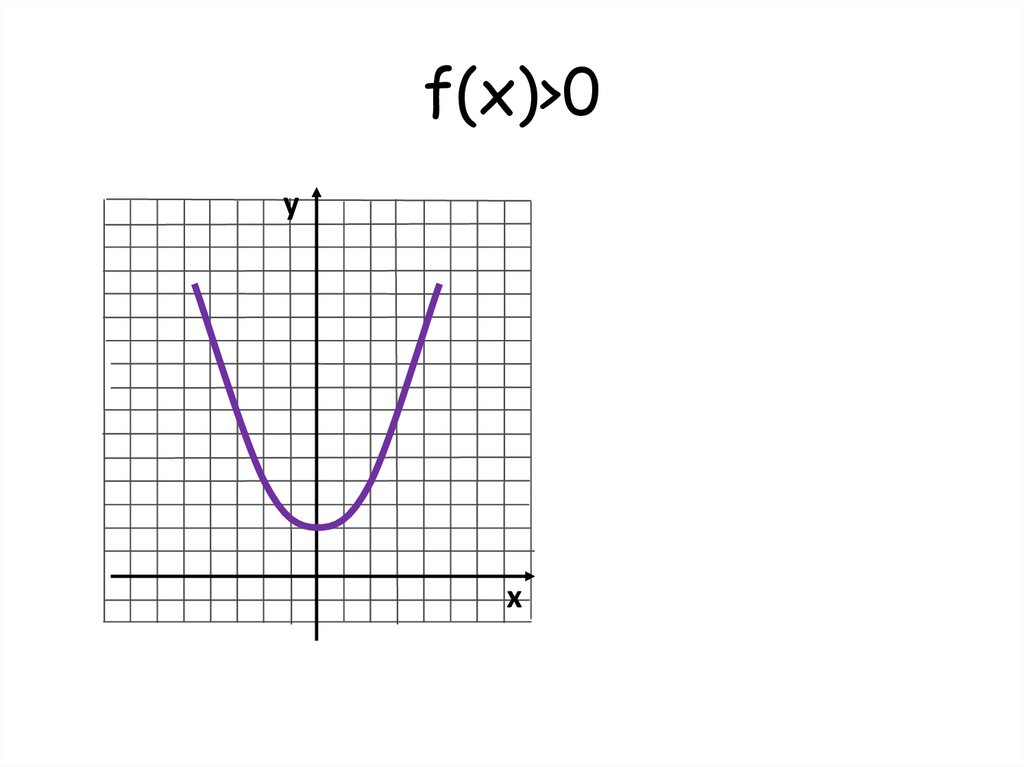
найди решение f(x) > 0, запиши ответ
у
х

6.

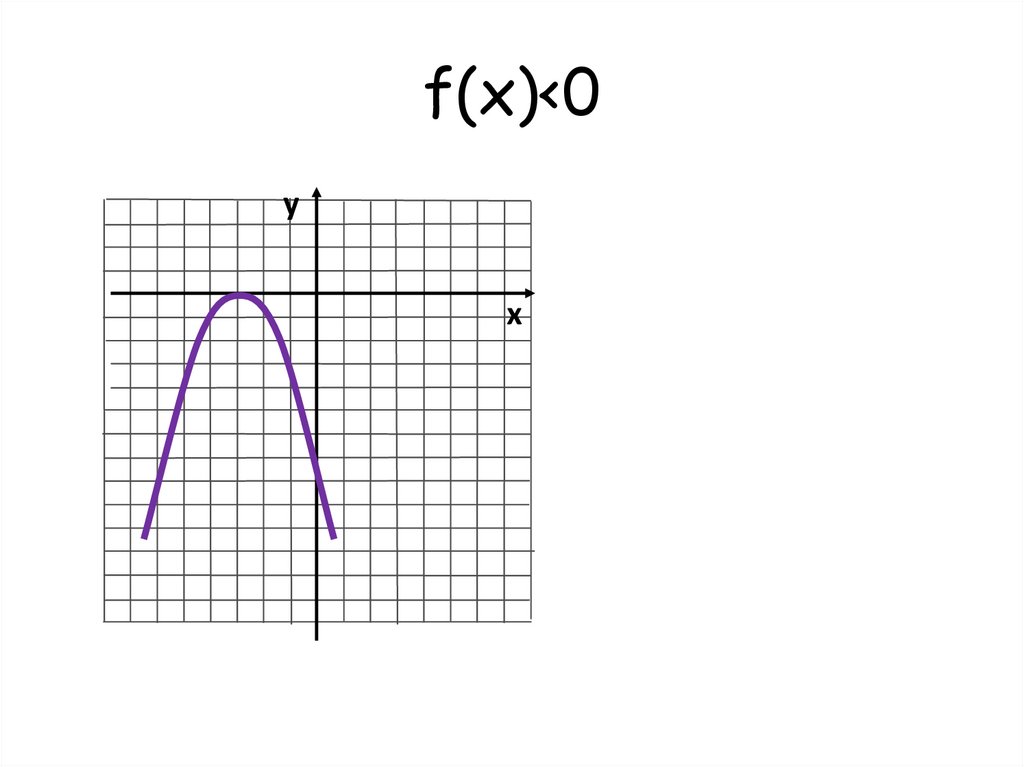
f(x)<0
у
х

7.

f(x)>0
у
х

8.

f(x)>0
у
х

9.

f(x)<0
у
х

10.

f(x)<0
у
х

11.

ответы
(1;5)
(- ∞ ;-2) U (2; +∞)
Решения нет
Любое число
Решения нет
( -∞ -2) U (-3; +∞)

12.

13.

Решение неравенства ах²+bх+с>0, используя график
квадратичной функции
D>0
D=0
D<0
a>0
X
x1
x1=x2
x2 X
–любое число,
x (-∞;x1)U(x2; +∞) xкроме
x1
a<0
x1
x2
x1=x2
X
x (-x1;x2)
x –любое число
X
X
Решений нет
Решений нет
X