Решение неравенств второй степени с одной переменной

1. Решение неравенств второй степени с одной переменной

Лицей философии планетарного гуманизма
Решение неравенств второй
степени с одной переменной
9класс
Учитель высшей категории М.Н.Ковшова
2011г

2. Цель:

Сформировать умения решать неравенства
ах² + вх +с >0 (ах² + вх +с ≥0 ),
ах² + вх +с < 0 (ах² + вх +с ≤ 0),
где а ≠ 0, с опорой на сведения о графике
квадратичной функции (направление ветвей
параболы, ее расположение относительно оси 0х).

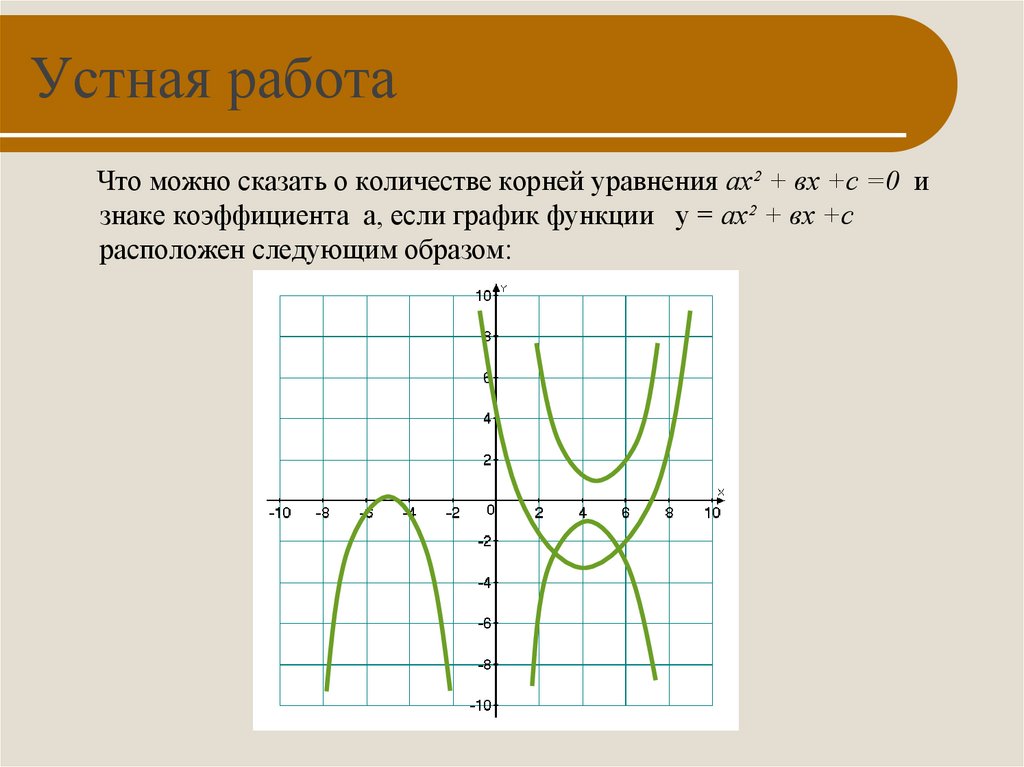
3. Устная работа

Что можно сказать о количестве корней уравнения ах² + вх +с =0 и
знаке коэффициента а, если график функции у = ах² + вх +с
расположен следующим образом:

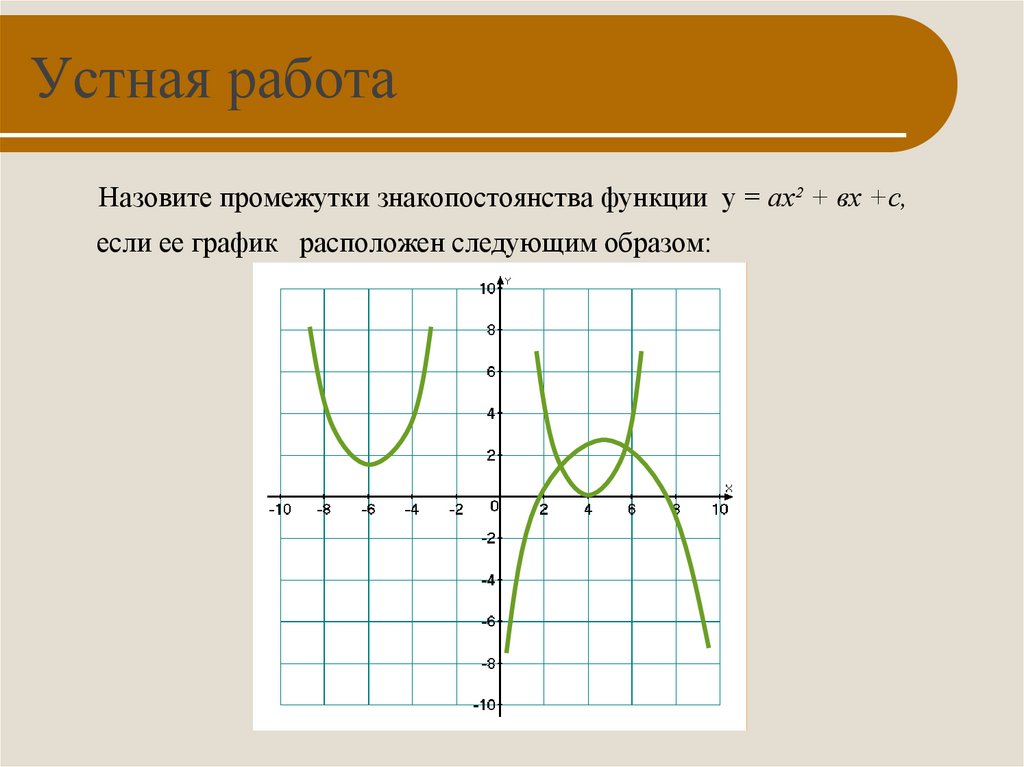
4. Устная работа

Назовите промежутки знакопостоянства функции у = ах² + вх +с,
если ее график расположен следующим образом:

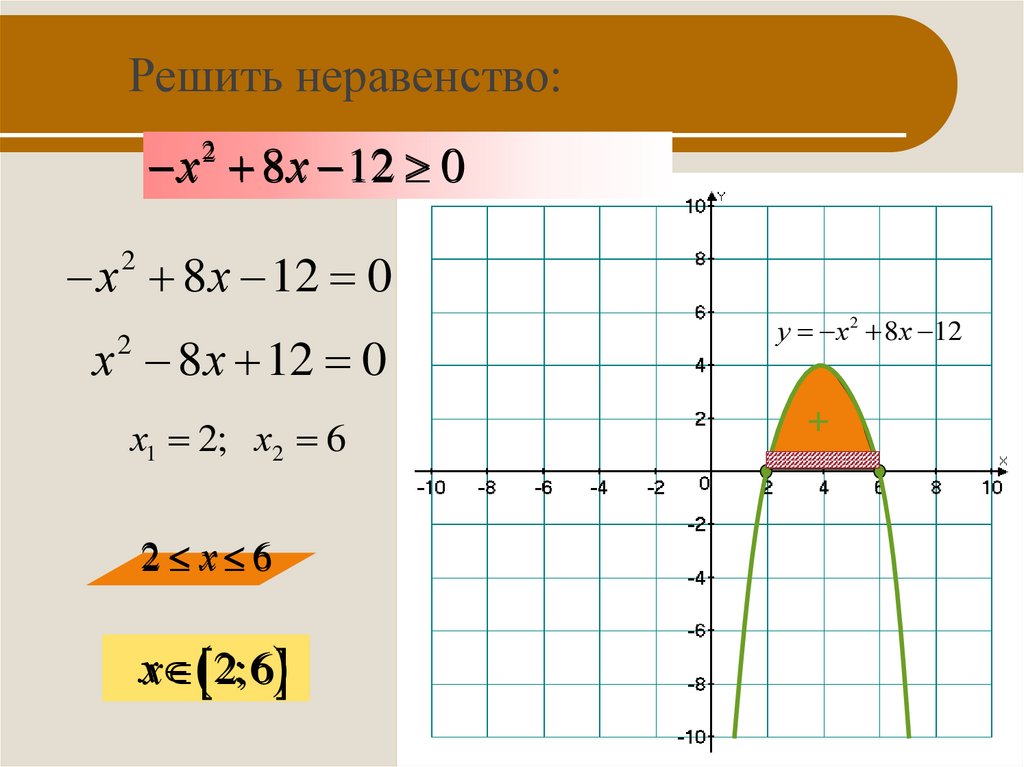
5. Решить неравенство:

х 8 х 12 0 х 8х 12 0
2
х 8 х 12 0
2
2
х1 2; х2 6
2
х
6
+
+
у х 2 8 х 12
х
х 2;6

6. Решить неравенство:

х 2 8 х 12 0 х 2 8 х 12 0
х 8 х 12 0
2
х1 2; х2 6
2, хх 66
х
+
+
у х 2 8 х 12
х ;2 6;
6;

7. Решить неравенство:

х 2 8 х 12
0
х 8 х 12 0
2
х 8 х 12 0
2
х1 2; х2 6
2
х
6
х
х 2;6
у х 2 8х 12
+

8. Решить неравенство:

х 2 8 х 12
0
х 8 х 12 0
2
у х 2 8х 12
х 8 х 12 0
2
+
х1 2; х2 6
2, х 66
хх 2,
х
х
;2
;2 6;
-
-

9. Решить неравенство:

х 4 х 4 0
22
у х2 4х 4
х 4х 4 0
2
D 0;
х 2
Нетхрешений
2
+
+

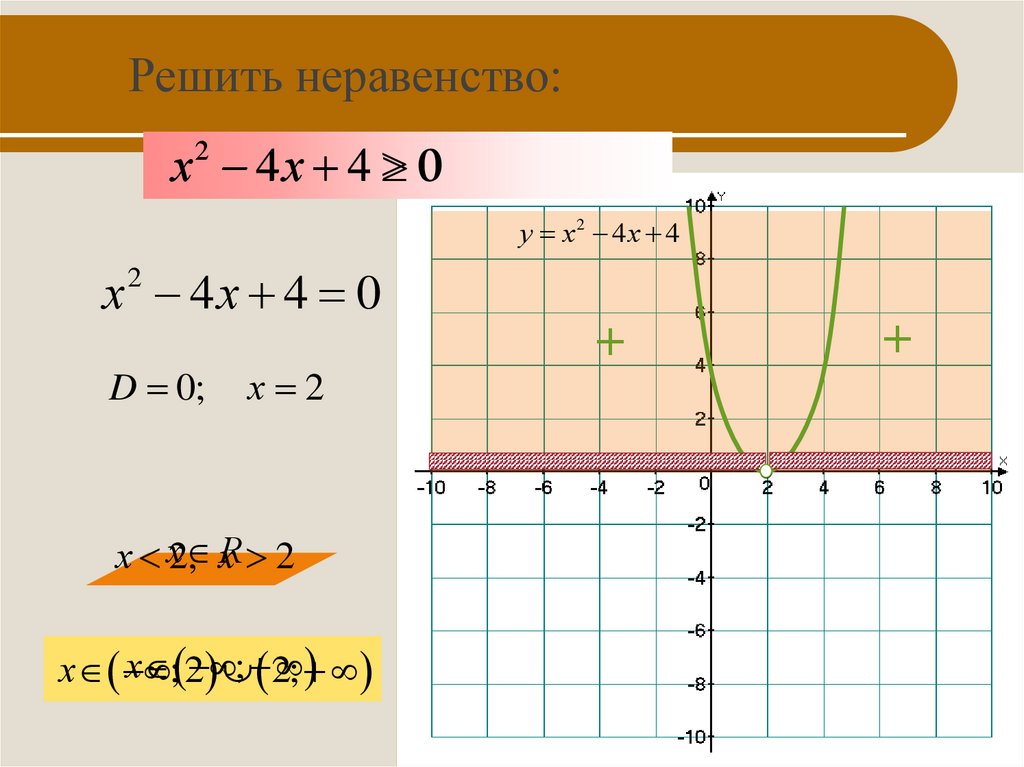
10. Решить неравенство:

х2 4 х 4
0
у х2 4х 4
х 4х 4 0
2
D 0;
х 2
х х2, хR 2
х ;2
х
; 2;
+
+

11. Решить неравенство:

х 4х 5 0 х 4х 5 0
2
х 4х 5 0
2
D 0
Нет решений
х R
2
у х2 4х 5
+
+

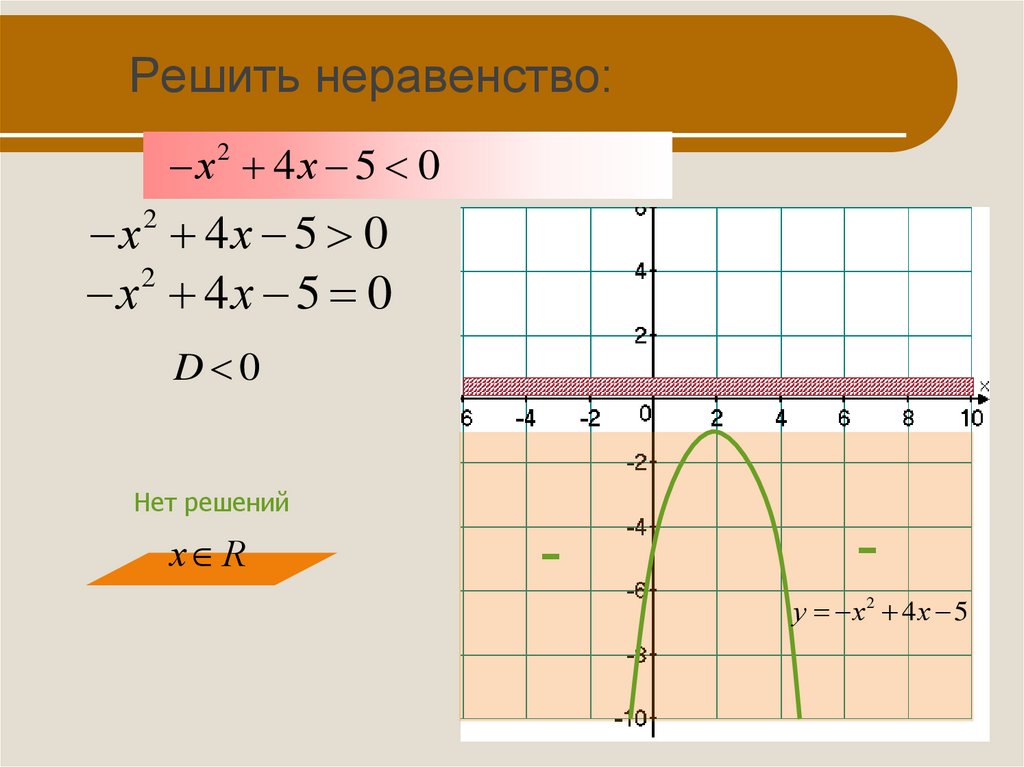
12. Решить неравенство:

х2 4х 5 0
х2 4х 5 0
2
х 4х 5 0
D 0
Нет решений
х R
-
у х2 4х 5

13. Для решения неравенств вида ах² + вх +с >0 и ах² + вх +с < 0 поступают следующим образом:

Для решения неравенств вида ах² + вх +с >0 и ах² + вх +с < 0
поступают следующим образом:
Находят дискриминант квадратного трехчлена и выясняют, имеет
ли трехчлен корни;
Если трехчлен имеет корни, то отмечают их на оси х и через
отмеченные точки проводят схематически параболу, ветви которой
направлены вверх при а >0 или вниз при а < 0; если трехчлен
не имеет корней, то схематически изображают параболу,
расположенную в верхней полуплоскости при а >0 и в нижней при
а < 0;
Находят на оси х промежутки, для которых точки параболы
расположены выше оси х ( если решают неравенство ах² + вх +с >0
или ниже оси х (если решают неравенство ах² + вх +с < 0).

14.

РЕШЕНИЕ НЕРАВЕНСТВ ВТОРОЙ СТЕПЕНИ С ОДНОЙ ПЕРЕМЕННОЙ
Автор составитель: учитель высшей
категории М.Н.Ковшова
2011 год

15. СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

АЛГЕБРА. Учебник для 9 класса общеобразовательных
учреждений под редакцией С.А. Теляковского. Авторы:
Ю.Н. Макарычев, И.Г. Миндюк, К.И. Нешков, С.Б.
Суворова. Москва «Просвещение» 2004
Алгебра. Поурочные планы по учебнику Ю.Н.
Макарычев и др./ авт.-сост. С.П. Ковалева.-Волгоград:
Учитель, 2005. – 316с. ISBN 5-7057-0666-9