Похожие презентации:
Определители матриц
1. Тема: «Определители»
2.
В ходе решения задач по высшей математикеочень часто возникает необходимость
вычислить определитель матрицы.
Определитель матрицы используется в
линейной алгебре, аналитической геометрии,
математическом анализе, поэтому без
навыка решения определителей просто не
обойтись.
3.
«Где это возможно, считайте!»Фрэнсис Гальтон (16.02.1822 – 17.01.1911)
английский исследователь, географ, психолог
4.
Определитель – это число,характеризующее квадратную
матрицу.
Обозначается:
A ,
, det A
5.
Определителем первого порядкаматрицы A (a11 ) называется число
a11 , то есть:
A a11 a11
Определителем второго порядка
матрицы А называется число, которое
определяется по правилу:
a11 a12
a11 a22 a12 a 21
a21 a22
6.
Определителем третьего порядканазывается число, которое
определяется по правилу:
a11 a12 a13
a21 a22 a23 a11 a22 a33 a12 a23 a31 a13 a21 a32
a31 a32 a33
a13 a22 a31 a12 a21 a33 a11 a23 a32
7.
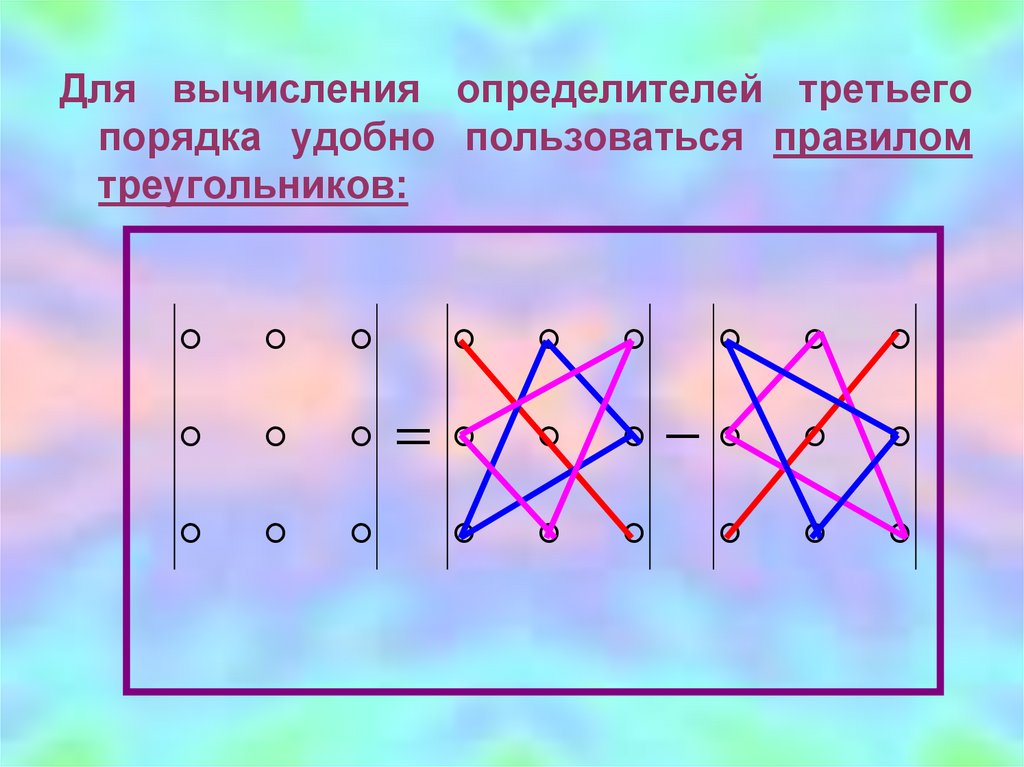
Для вычисления определителей третьегопорядка удобно пользоваться правилом
треугольников:
8.
Вычислить определители матриц:1 2
A
3 5
1 1 1
B 2 1 1
1 1 2
1 2
A
1 5 ( 3) 2 11
3 5
1 1 1
B 2 1 1 1 1 2 ( 1) 1 1 1 2 1 1 1 1 ( 1) 2 2 1 1 1 5
1 1 2
9.
Минором некоторого элементаопределителя называется определитель,
полученный из исходного вычеркиванием строки
и столбца, на пересечении которых стоит
данный элемент.
Минор элемента определителя a ij обозначается как
M ij
Алгебраическим дополнением некоторого
элемента определителя называется минор
этого элемента, умноженный на (-1)S ,
где S – сумма номеров строки и столбца, на
пересечении которых стоит данный элемент.
Aij ( 1) M ij
S
S i j
10.
В частности, минор элементаa11
определителя третьего порядка найдется по
правилу:
a11 a12
a21 a22
a31 a32
a13
a23
a33
a22
M 11
a32
Его алгебраическое дополнение:
1 1
A11 ( 1) M11 M11
a23
a33
11.
Вычислить определитель:Раскладываем
определитель по третьей строке:
1
1
0
2
2
2
1
3
3
3
1
4
1
1
0
2
2
2
1
3
3
3
1
4
4
1
0
1
4
1
0 A31 1 A32 1 A33 0 A34 A32 A33
=
0
1
Находим алгебраические дополнения:
1 3 4
A32 ( 1)3 2 M 32 1 3 1 (3 6 16 24 3 4) 6
2 4 1
1 2 4
A33 ( 1)3 3 M 33 1 2 1 2 4 12 16 2 3 3
2 3 1
Подставляем полученный результат:
= 6 ( 3) 3
12.
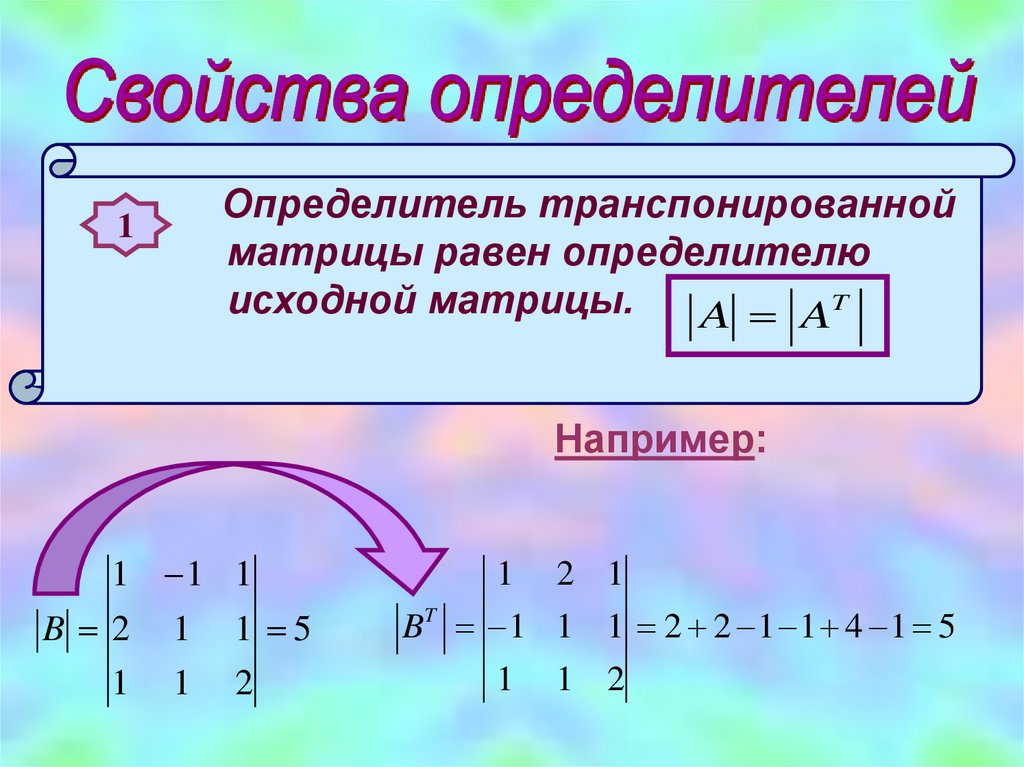
1Определитель транспонированной
матрицы равен определителю
исходной матрицы.
A AT
Например:
1 1 1
B 2 1 1 5
1 1 2
1 2 1
BT 1 1 1 2 2 1 1 4 1 5
1 1 2
13.
2Например:
Перестановка двух строк или
столбцов определителя
эквивалентна умножению его
на (-1).
1 1 1
B 2 1 1 5
1 1 2
Меняем местами первую и вторую строки:
2 1 1
1 1 1 4 1 1 1 2 2 5
1 1 2
14.
3Если определитель имеет две
одинаковые строки или столбца,
то он равен нулю.
Например:
1 1 3
2 2 2 4 4 12 12 4 4 0
2 2 2
15.
4Общий множитель строки или
столбца можно выносить за знак
определителя.
Например:
1 1 1
2 2 2 4 2 2 2 4 2 4
1 1 2
Выносим из второй строки множитель 2:
1 1 1
1 1 1
2 2 2 2 1 1 1 2 (2 1 1 1 2 1) 2 2 4
1 1 2
1 1 2
16.
Определитель не изменится, еслик элементам одной строки или столбца
прибавить соответственные элемент
другой строки или столбца, умноженные
на одно и то же число.
5
Например:
1 1 1
B 2 1 1 5
1 1 2
1
Первую строку
умножаем на 2
4
и складываем со второй: 1
1 1
1 3 2 3 4 1 8 3 5
1 2
17.
Потренироваться, раскрыть, провестирасчёты — это очень хорошо и полезно. Но
сколько времени вы потратите на большой
определитель? Нельзя ли как-нибудь
быстрее и надёжнее?
Оказывается, время, которое потратится
на вычисления определителя, зависит от
вашего опыта и от знаний свойств
определителей.
18.
Рациональные приёмы, упрощающие вычисления:– треугольный определитель равен произведению чисел его
главной диагонали;
– чтобы избавиться от «минуса» перед определителем,
рациональнее поменять местами любые две строки или любые
два столбца.
– определитель выгоднее раскрывать по ТОЙ строке(столбцу),
где нулей побольше и числа поменьше.
19.
Подводя итоги мы можем суверенностью сказать, что
мы научились вычислять
определители разных
порядков , повторили правила
и возможности упрощения
вычислений определителей
порядка выше третьего.

















 Математика
Математика








