Характеристики НСВ

1. Урок 23   Тема : Характеристики НСВ

Урок 23
Тема : Характеристики НСВ

2. Основные вопросы темы:

1. Мода, медиана, квантили
2. Начальные и центральные
моменты
3. Асимметрия и эксцесс
4. Математическое ожидание,
дисперсия

3. 1. Мода и медиана. Квантили

Кроме математического ожидания и дисперсии,
в теории вероятностей применяется еще ряд
числовых характеристик, отражающих те или
иные особенности распределения.
Модой Мо(Х) случайной величины Х называется
ее наиболее вероятное значение (для которого
вероятность pi или плотность вероятности φ(х)
достигает максимума).
Медианой Ме(Х) непрерывной случайной
величины Х называется такое ее значение, для
которого
P(X < Me(X)) = P(X > Mе(X)) = 1/2,
т. е. вероятность того, что случайная величина Х
примет значение, меньшее медианы Ме(Х) или
большее ее, одна и та же и равна ½.

4. 1. Мода и медиана. Квантили

Квантилем уровня q (или qквантилем) называется такое значение
хq случайной величины, при котором
функция ее распределения принимает
значение, равное q, т. е.
F(xq) = P(X < xq) = q.
Некоторые квантили получили особое
название.
Очевидно, что введенная выше медиана
случайной величины есть квантиль
уровня 0,5, т. е. Ме(Х) = х 0,5.

5. 2. Начальные и центральные моменты.

Начальным моментом k-го порядка
случайной величины Х называется
математическое ожидание k-й степени этой
величины:
νk = M(Xk).
Центральным моментом k-го порядка
случайной величины Х называется
математическое ожидание k-й степени
отклонения случайной величины Х от ее
математического ожидания:
μk = M[X – M(X)]k или
μk = M(X – а)k, где а = М(Х).

6. 2. Начальные и центральные моменты.

Нетрудно заметить, что при k = 1 первый
начальный момент случайной
величины Х есть ее математическое
ожидание, т. е.
ν1 = М(Х) = а,
при k = 2 второй центральный момент –
дисперсия, т. е.
μ2 = D(X)

7. 3. Асимметрия и эксцесс

Математическое ожидание М(Х), или
первый начальный момент,
характеризует среднее значение или
положение распределения случайной
величины Х;
Дисперсия D(X), или второй
центральный момент μ2, – степень
рассеяния распределения Х
относительно М(Х). Для более
подробного описания распределения
служат моменты высших порядков.

8. 3. Асимметрия и эксцесс

Третий центральный момент μ3 служит для
характеристики асимметрии (скошенности)
распределения. Он имеет размерность куба случайной
величины. Чтобы получить безразмерную величину, ее
делят на σ3, где σ – среднее квадратическое отклонение
случайной величины Х. Полученная величина А
называется коэффициентом асимметрии случайной
величины:
А
3
3
Если распределение симметрично относительно
математического ожидания, то коэффициент
асимметрии А = 0.

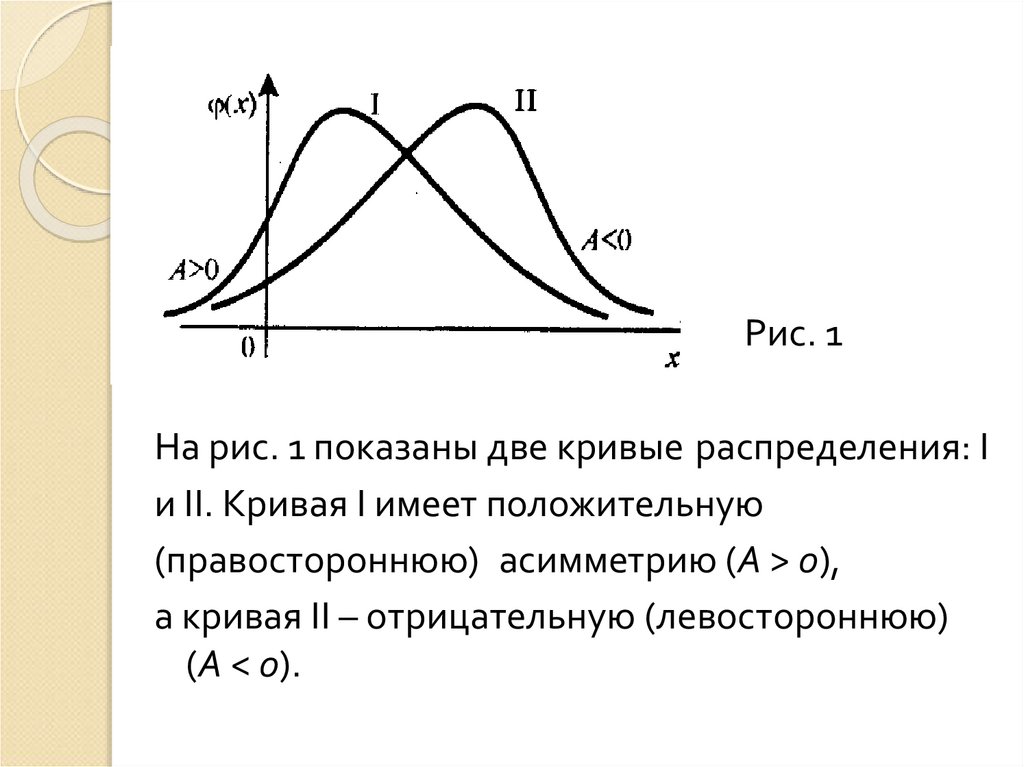
9.

Рис. 1
На рис. 1 показаны две кривые распределения: I
и II. Кривая I имеет положительную
(правостороннюю) асимметрию (А > 0),
а кривая II – отрицательную (левостороннюю)
(А < 0).

10.

Четвертый центральный момент μ4
служит для характеристики крутости
(островершинности или плосковершинности)
распределения.
Эксцессом случайной величины называется
число
Е
4
4
-3
(Число 3 вычитается из отношения μ4/σ4
потому, что для наиболее часто
встречающегося нормального распределения
отношение μ4/σ4 = 3.

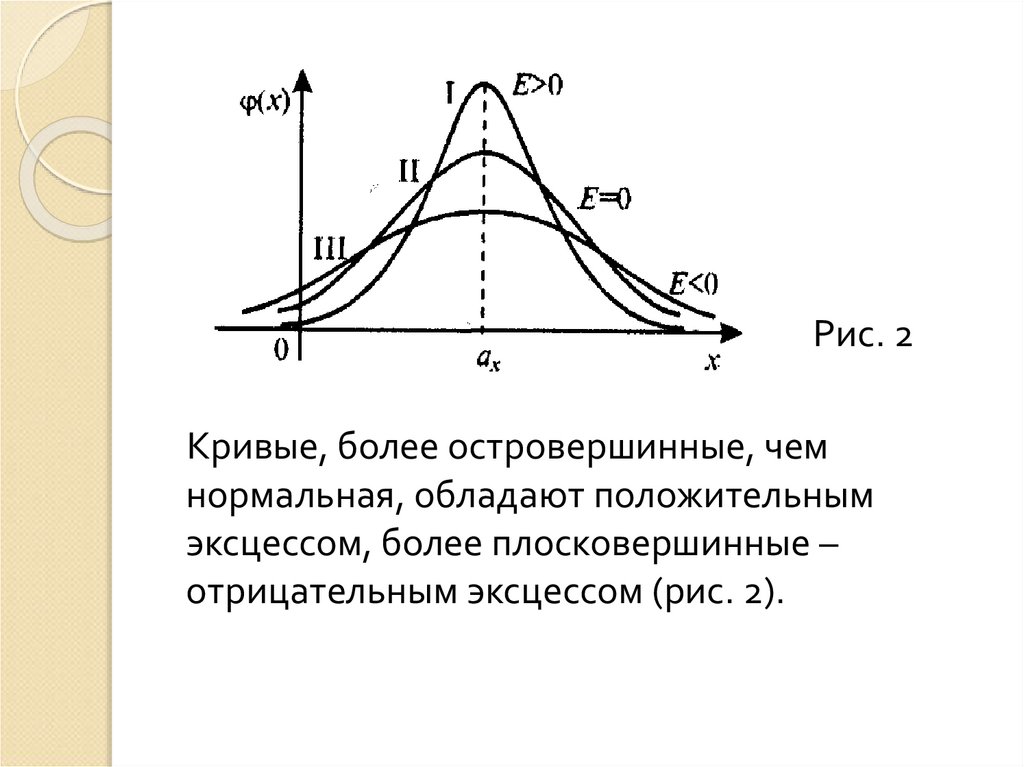
11.

Рис. 2
Кривые, более островершинные, чем
нормальная, обладают положительным
эксцессом, более плосковершинные –
отрицательным эксцессом (рис. 2).

12. 4. Математическое ожидание М(Х) и дисперсия D(X)

Формулы для математического ожидания и дисперсии
непрерывной случайной величины Х:
a M(X) x ( x)dx
-
D( X ) M ( X ) a
2
2
D(X) x (x) dx - a
2
-
2

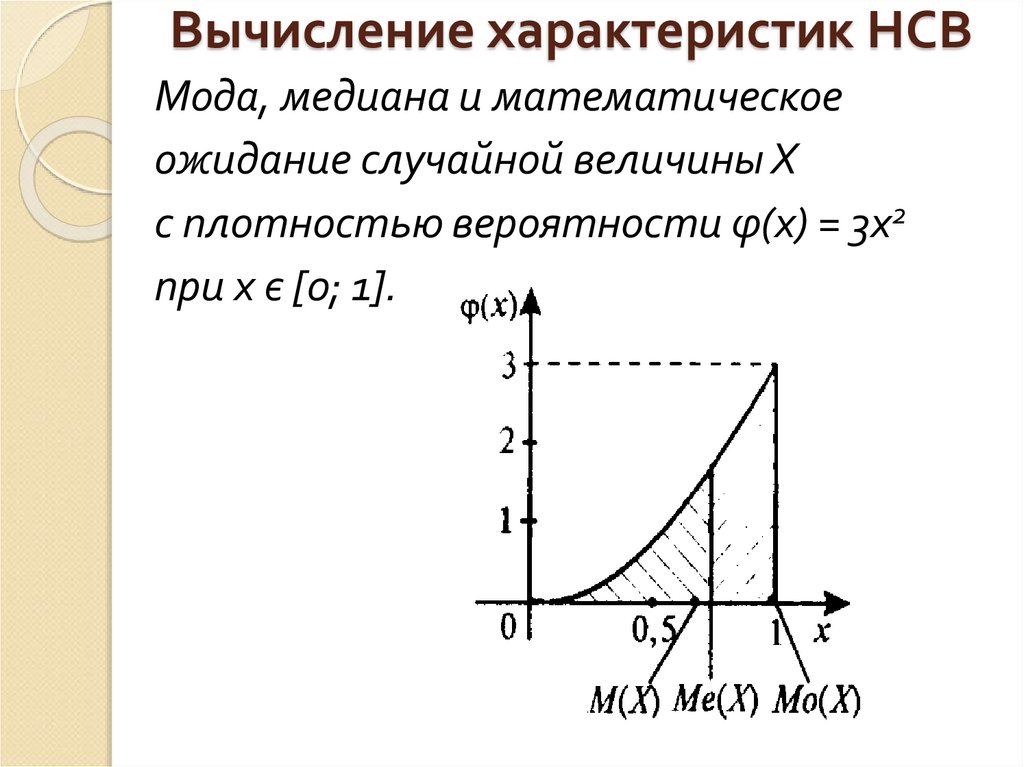
13. Вычисление характеристик НСВ

Задача 1
Найти моду, медиану и
математическое ожидание случайной
величины Х с плотностью
вероятности φ(х) = 3х2 при х є [0; 1].

14.

Очевидно, что плотность вероятности φ(х)
максимальна при
х = Мо(Х) = 1.
Медиану Ме(Х) = b найдем из условия:
b
( x)dx 1 / 2
b
0
b
( x)dx 0 dx 3x dx x
2
3 b
0
b 1/ 2
0
b Me( X ) 3 1 / 2 0,79
3

15. Вычисление характеристик НСВ

Мода, медиана и математическое
ожидание случайной величины Х
с плотностью вероятности φ(х) = 3х2
при х є [0; 1].

16. Задача 2

Функция φ(х) задана в виде:
при x 1
0
( x) 4
3 / x при x 1
Найти: M(X), D(X)

17. Задача 2

Функция φ(х) задана в виде:
при x 1
0
( x) 4
3 / x при x 1
Найти: M(X), D(X)
Решение
Найдем математическое ожидание по формуле
а М(Х) х ( x)dx
-
b
b
3 1 3
3
dx
1
M ( X ) 0 dx x 4 dx 0 3 lim 3 3 lim 2 lim 1 2
2 b b 2
b x
b 2 x
1
1 x
1
1
Дисперсию D(X) вычислим по формуле
D( X ) M ( X 2 ) a 2
Вначале найдем
M(X )
2
-
x (x)dx
2
Теперь D(X) = 3 – (3/2)2 = 3 – 9/4 = 3/4
Ответ: M(X)= 3/2, D(X) = 3/4
-
х2 (
3
) dx 3
4
х

18. Домашнее задание

Калинина В. Н.
Глава 5. Случайные величины.
§ 5.5 Числовые характеристики случайной
величины.
Конспект по теме гл. 5 § 5.5, вопросы к
теме
Решение упражнений [1] гл. 5, § 5.5,
№ 5.8, 5.10

19. Вопросы к теме

1. Как называют квантиль уровня 0,5?
.........................................................................................
2. Как называют первый начальный момент?
.........................................................................................
3. Чему равен первый центральный момент?
.........................................................................................
4. Что показывает второй центральный момент?
.........................................................................................
5. Что показывает третий центральный момент?
.........................................................................................
6. Что показывает четвертый центральный момент?
.........................................................................................

20. Домашнее задание

Задача
Функция распределения случайной величины X
имеет вид
при x 0,
0
F ( X ) x / 3 при 0 x 3
1
при x 3
Найти: M(X), D(X)