Числовые характеристики СВ

1. Примеры

Задан график функции плотности распределения
f(x)
с
1
x
Найти: 1) с , 2) функцию распределения, 3) P(0,5 4)

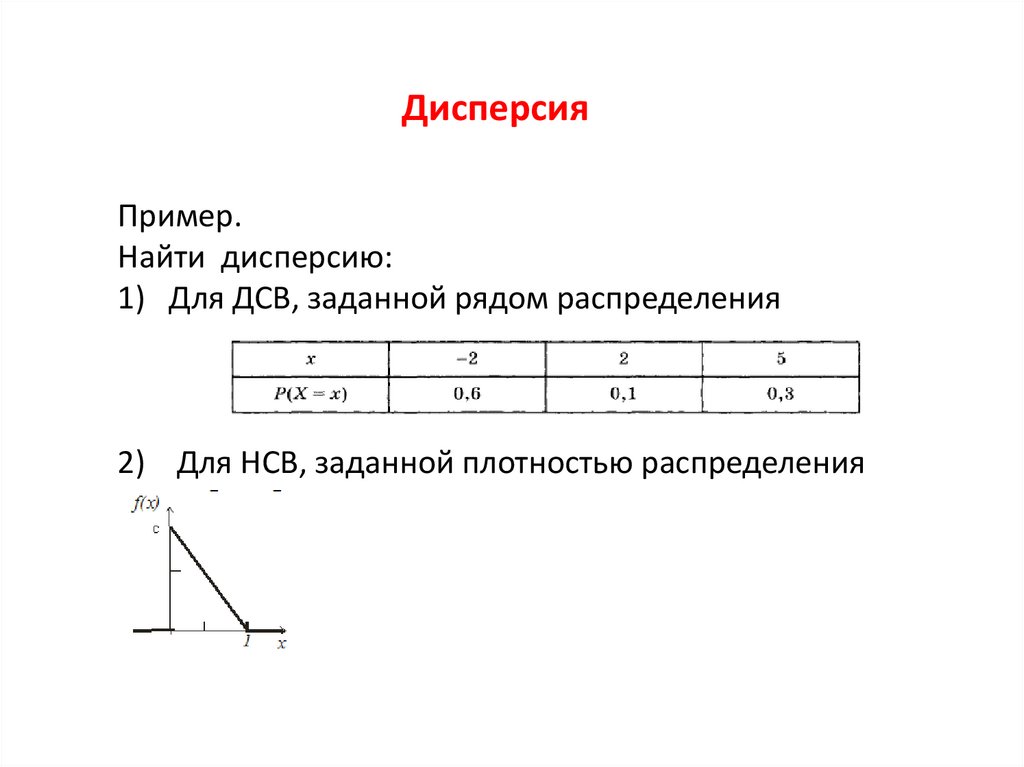
2. Числовые характеристики СВ

Числовые параметры, характеризующие существенные
свойства закона распределения СВ, называют
числовыми характеристиками.

3.

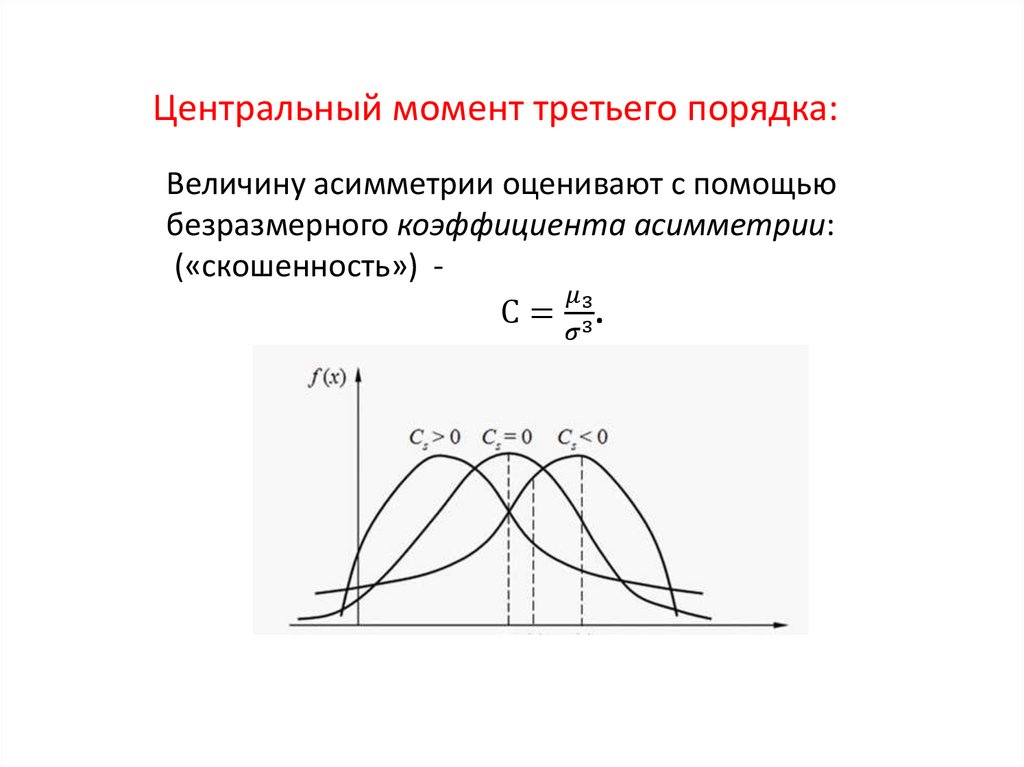
ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
Начальные моменты
Центральные моменты

4. Начальный момент

Начальным моментом m -го порядка случайной величины
называют число:
n
m xim pi для дискретных случайных величин,
i 1
m x m f ( x)dx для непрерывных случайных величин.

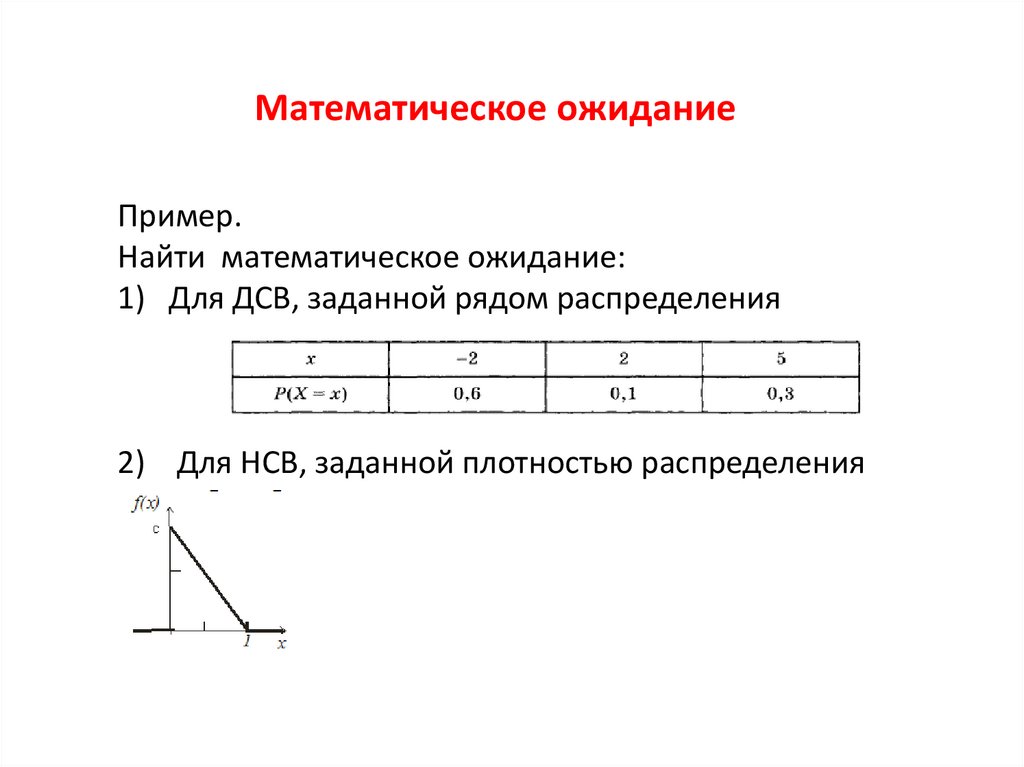
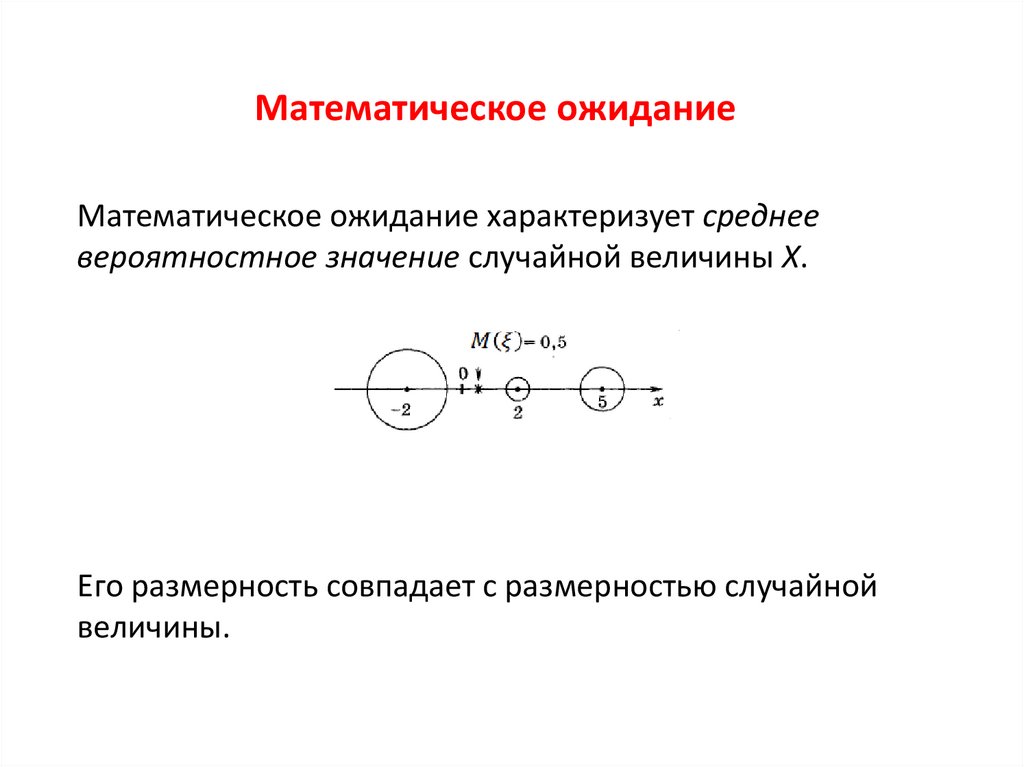
5. Математическое ожидание

Первый начальный момент 1
называют математическим
ожиданием случайной величины и обозначают m или M ( )